3702

УДК 681.518:076.5

АНАЛИЗ РЕШЕНИЯ ПЛАНА ВЫПУСКА ИЗДЕЛИЙ

А.А. Катрахова, В.С.Купцов, А.Р. Кылымыстый, К.И. Чеботок

Воронежский государственный технический университет kafedra@vmfmm.vorstu.ru

В работе произведен анализ решения плана выпуска изделий, обеспечивающего максимальную прибыль от их реализации

Ключевые слова: метод множителей Лагранжа, анализ, экстремум

Проанализируем количество изделий, которое надо выпустить, чтобы прибыль была максимальна. Для объяснения анализа решения плана выпуска изделий, применяется метод множителей Лагранжа. Обозначив через х1 и х2 плиту и перемычку. В качестве функции f(x1, x2) возьмем суммарную сумму: f(x1, x2)=30x1+19x2. Запас сырья примем за ограничения, накладываемые на переменные x1, x2.

В указанной постановке решаемая задача может быть сформулирована как задача поиска условного экстремума:

30x1+19x2→max;

7x1+5x2≤70; 9x1+4x2≤80; 2x1+2x2≤30; x1≥0; x2≥0.

Решим задачу методом множителей Лагранжа: 1. Приведем ограничения к виду φ(x)≤0:

70–7x1–5x2≤0; 80–9x1–4x2≤0; 30–2x1–2x2≤0; –x1≤0; –x2≤0.

2. Путем введения дополнительных переменных x1, x2, x3, x4, x5, x6, x7 перейдем к ограничениям-равенствам:

70–7x1–5x2+x32=0; 80–9x1–4x2+x42=0; 30–2x1–2x2+x52=0;

–x1+x62=0; –x2+x72=0.

3. Сформируем функцию Лагранжа:

110

Ф(x1, x2, x3, x4, x5, x6, x7, λ1, λ2, λ3, λ4, λ5) = 30x1+49x2λ1(70–7x1–5x2+x32)+

+λ2(80–9x1–4x2+x42)+λ3(30–2x1–2x2+x52)+λ4(–x1+x62)+λ5(–x2+x72).

4.Составим необходимые условия Ф(Х, Λ) = 0:

средств математического пакета Mathcad. В результате использования приведенной программы было получено следующее решение: x1=4, x2=11, f(x1, x2)=329.

Необходимо отметить, что значительный размер сформированной системы уравнений, полученных из необходимых условий (12 уравнений), вызван во-первых, тем, что переход от ограничений-неравенств к ограничениямравенствам осуществляется путем введения дополнительных переменных х3, х4, х5, х6, х7, число которых равно числу ограничений-неравенств; во-вторых, с тем, что переход от задачи нахождения условного экстремума к задаче безусловного поиска возможен, в соответствии с методом Лагранжа, с помощью введения дополнительных переменных 1, 2, 3, 4, 5, число которых равно общему числу ограничений задачи.

Таким образом, решение задачи методом Лагранжа получено ценой повышения ее размерности. Этот недостаток ограничивает область применения метода Лагранжа сравнительно простыми задачами, поэтому с повышением числа переменных и ограничений целесообразно переходить к численным методам математического программирования.

Для проверки правильности полученных результатов проведем анализ решения. Переписав исходную систему ограничений неравенств в виде

111

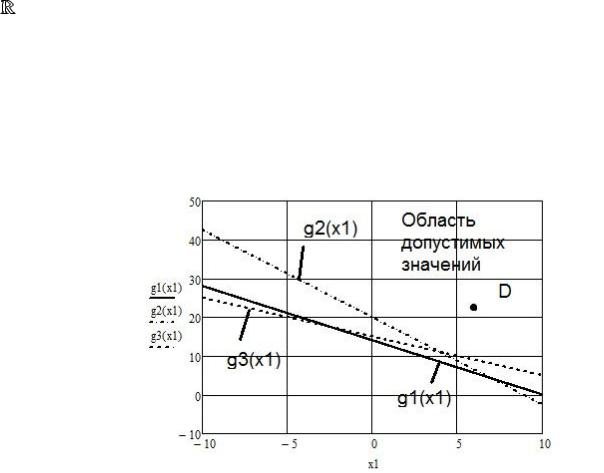
Получаем возможность графически представить эти ограничения на плоскости Оху в виде прямых g1(x1); g2(x1); g3(x1). Как следует из графика, область допустимых решений не является замкнутой, допустимые значения x1x2 не ограничены сверху, и любая пара их допустимых значений, например, точка D, соответствует плану выпуска изделий, который обеспечил бы максимальную прибыль от реализации.

Для объяснения анализа решения плана выпуска изделий применялся метод множителей Лагранжа, используемый для решения задач математического программирования (в частности, линейного программирования) – метод нахождения условного экстремума функции f(x), где x n, относительно m ограничений µi(x)=0, где i меняется от единицы до m. Как показало решение, метод множителей Лагранжа довольно трудоемкий, так как имеется необходимость повысить число переменных и ограничений. Этот недостаток значительно уменьшает область применения этого метода.

Литература

1.Смирнов В.И. Курс высшей математики. М.: Наука, 1974, Т.1, 479 с.

2.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. M.: Нау-

ка, 2007. Т.1. 607 c.

2.Вентцель Е.С. Исследование операций / Е.С. Вентцель. М.: Дрофа, 2004. 208 c.

3.Катрахова А.А. Основы численных методов: учеб. пособие / А.А. Катрахова, М.П. Семенов. Воронеж: ВГТУ, 2004.

ANALYSIS OF THE SOLUTION TO THE PLAN

FOR THE RELEASE OF PRODUCTS

А.А. Katrachowa, W.S. Kuptsov, A.R. Kylymysty, K.I. Chebotock

Voronezh State Technical University

The analysis of the decision of the plan of release of products providing the maximum profit from their realization is made

Keywords: method of Lagrange multipliers, analysis, extremum

112

УДК 519.632: 004.94

ИССЛЕДОВАНИЕ ТРЕХПОЗИЦИОННОГО РЕЛЕ С ГИСТЕРЕЗИСОМ И ЗОНОЙ НЕЧУВСТВИТЕЛЬНОСТИ

А.А. Катрахова, В.С. Купцов, И.В. Енин, Е.Р. Евтушенко

Воронежский государственный технический университет kafedra@vmfmm.vorstu.ru

В работе произведен графо-аналитический анализ сигнала на выходе трехпозиционного реле с гистерезисом

Ключевые слова: нелинейная система, фазовый портрет, метод Эйлера

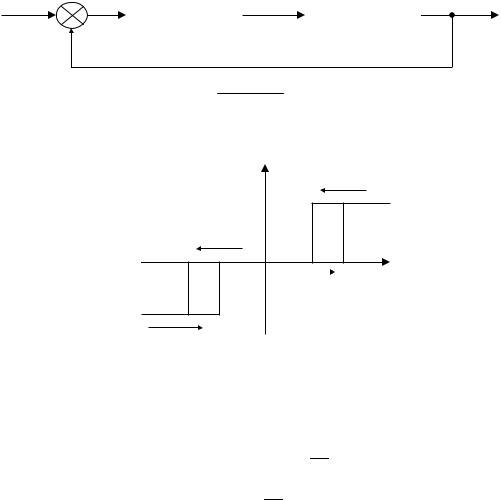
Построен переходный процесс (t), возникающий в нелинейной системе автоматического регулирования, представленной на рис. 1, при подаче на ее вход ступенчатого воздействия g(t) = 5. Получен фазовый портрет системы, который дает представление о совокупности всех возможных состояний системы и типах возможных движений в ней.

W (p) 10

F( )

12

3 4

Рис. 1

Запишем уравнения для данного звена в нормальной форме Коши:

̇= −5 ( ), ̇= − 4 ,= 4 + .

113

Для численного решения системы уравнений использовался метод Эйлера с шагом h:

= 4, + .

Функцию F( ) зададим путем разбиения области ее определения на интервалы, в которых она описывается элементарными функциями:

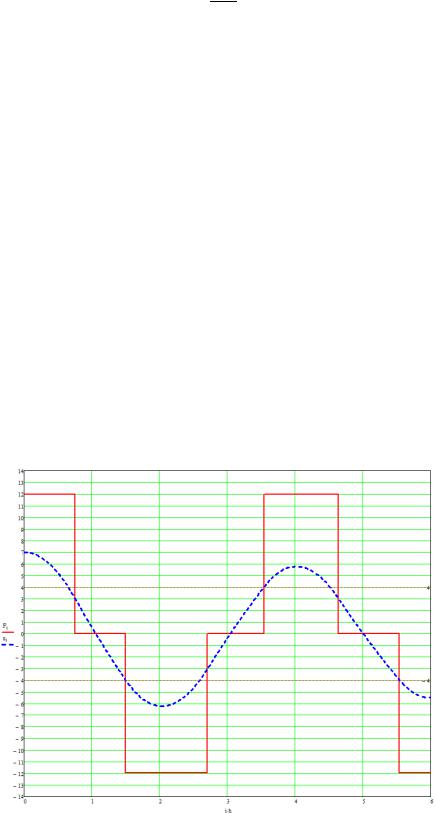
На основе вычислений получен график переходных процессов, показанный на рис. 2, и фазовый портрет (рис. 3).

На графике показан процесс изменения сигнала (t) системы при подаче на вход задающего воздействия g(t) = 7. Результат решения существенно зависит от амплитуды задающего воздействия g(t).

На графике видны такие свойства системы, как гистерезис и наличие зоны нечувствительности. Также прослеживается наличие отрицательной обратной связи. На фазовом портрете (рис. 3) четко видны линии переключения при значении аргумента = –4; –3; 3; 4 (показаны пунктиром). В местах переключения линии годографа изламываются. Между линиями с = –4; –3 и = 3; 4 наблюдается эффект гистерезиса. Это значит, что порог включения не равен порогу выключения. В данном случае порог гистерезиса равен 0,5.

Рис. 2 114

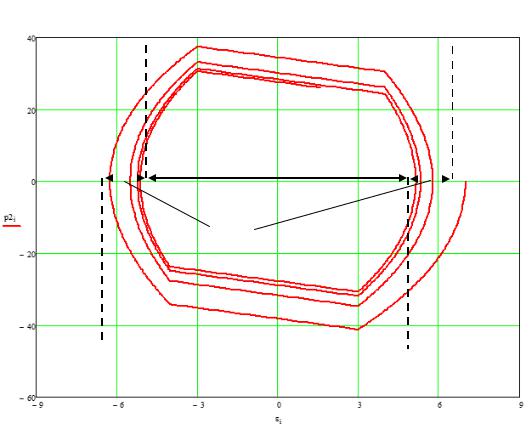
Зона нечувствительности

гистерезис

Рис. 3

Литература

1.Теория автоматического управления. Учеб. для вузов. В 2-х ч. Ч. II. / Под ред. А.В. Нетушила. М.: Высш. шк., 1972. 432 с.

2.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. M.: Нау-

ка, 2007. Т.1. 607 c.

3.Морозовский В.Т. Многосвязные системы автоматического регулирования. М.:

Энергия, 1970. 288 с.

4.Яковлева В.Б. Теория автоматического управления / В.Б. Яковлева. М.: Высш. шк., 2003. 567 c.

STUDY OF A THREE-POSITION RELAY

WITH HYSTERESIS AND A DEAD ZONE

А.А. Katrachowa, W.S. Kuptsov, I.V. Enin, E.R. Evtushenko

Voronezh State Technical University

Performed graph-analytical analysis of the signal at the output of non-linear element, which is fed to the input of the harmonic signal

Keywords: non-linear system, phase, Euler’s method

115

УДК 502.001.573(075.8)

АНАЛИЗ БЕЗОПАСНОСТИ ТЕХНИЧЕСКИХ ОБЪЕКТОВ В УСЛОВИЯХ РИСКОВЫХ СИТУАЦИЙ

И.Н. Пантелеев

Воронежский государственный технический университет vmfmm@mail.ru

Рассмотрено потенциально возможное воздействие на объект, направленное на нарушение его безопасности. Проведен анализ параметров систем защиты технических объектов в условиях рисковых ситуаций и угроз. Показано, что управление параметрами систем защиты технических объектов предполагает минимизацию общего риска угроз безопасности объекта; оптимальный выбор показателей системы защиты; декомпозицию общего риска и его распределение по отдельным угрозам

Ключевые слова: моделирование и оптимизация, анализ рисков

Рассмотрим вероятностную модель для оценки общего риска угроз безопасности объекта [1-4]. Эта модель основана на известных положениях теории надежности систем с последовательным соединением независимых элементов.

Под управлением параметрами систем защиты технических объектов будем понимать реализацию совокупности следующих воздействий на процессы проектирования, отработки и эксплуатации объекта:

–минимизация общего риска угроз безопасности технического объекта;

–оптимальный выбор показателей системы защиты;

–выбор интервальных ограничений на показатели системы защиты;

–декомпозиция общего риска объекта по совокупности отдельных угроз. Под угрозой на заданном отрезке [0, T] времени понимается потенциаль-

но возможное воздействие на объект, направленное на нарушение его безопасности. Угроза считается случайным событием. Предполагается, что множество угроз образует поле случайных событий в обычном смысле.

Пусть известны число п угроз безопасности и сами эти угрозы, которые

далее обозначаются как случайные события A1,A2,...,An . Угроза называется крупной, если ее реализация может нанести недопустимый ущерб безопасности

системы в целом. Обозначим через A событие, состоящее в реализации недопустимой общей угрозы на отрезке [0, Т] для данной системы.

Тогда в силу определения крупной угрозы имеем

A = n Ai ,

i 1

т.е. недопустимая общая угроза A на отрезке [0, T] реализуется только в том случае, когда реализуется хотя бы одна из крупных угроз Ai на том же отрезке времени. Отсюда для противоположных событий с учетом закона де Моргана находим

116

представляет собой вероятность возникновения на [0, T] угрозы Ai при условии

не возникновения угроз с меньшими номерами.

Частным риском на отрезке времени [0, T] называется безусловная вероятность

qi P(Ai )

где множества

попарно не пересекаются, приходим к известному соотношению

n

qqi ,

i1

в котором

i 1

qi P(Ai*) qi pj

j 1

– вероятность возникновения на [0, T] угрозы Ai и не возникновения угроз с меньшими номерами, а вероятности pj 1 qj . Здесь, как отмечалось, считает-

ся, что события Ai независимы.

117

называется верхней границей общего риска.

Далее предполагается, что безопасность технического объекта на заданном отрезке [0, T] времени обеспечивается системой защиты, а x1,x2,...,xm – ее параметры (показатели) на [0, T], причем

x=(x1, x2,..., xm)T

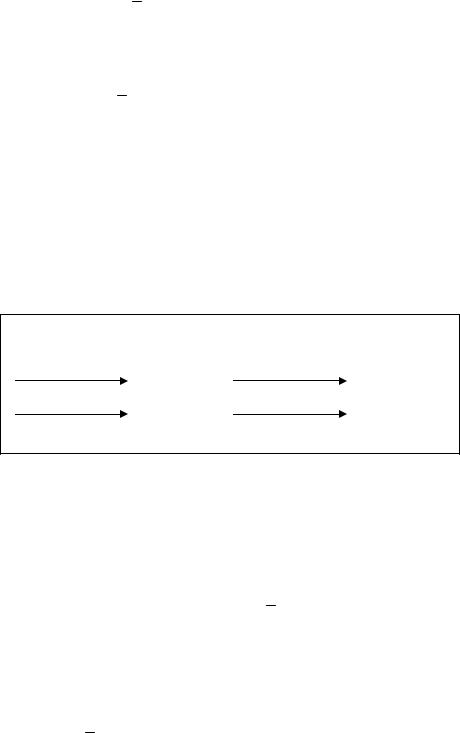
–вектор указанных показателей (см. рисунок).

Экспоненциальная модель общего риска

Зависимость частного риска qi объекта от показателей защиты на задан-

на заданном отрезке времени [0, T] по параметрам х системы защиты сводится к минимизации по х суммы

n n

yqi u(x)i

i1 i 1

частных рисков qi P(Ai ) ui (x) на [0, T].

118

Данная задача может быть решена в рамках системного интервального анализа методами нелинейного математического программирования. При этом решение задачи по управлению параметрами систем защиты технических объектов предполагает:

–разработку моделей общего риска и выбор целевой функции;

–минимизацию общего риска угроз безопасности объекта;

–оптимальный выбор показателей системы защиты;

–интервальный анализ общего риска объекта и обоснование требований

кпоказателям системы защиты;

–декомпозицию общего риска и его распределение по отдельным угро-

зам;

–сравнительную оценку и коррекцию проектов обеспечения безопасности сложных объектов.

Литература

1.Пантелеев И.Н., Пантелеев А.И. Математическое моделирование распространения облаков тяжелых газов при техногенных авариях // Сб. тр. VI межд. конф. ПМТУКТ-2013. -

Воронеж: изд-во ВГУ, 2013. С. 184-185.

2.Пантелеев И.Н., Пантелеев А.И. Моделирование распространения облаков тяжелых газов при техногенных авариях // Сб. ст. VIII Междунар. научн.-техн. конф. АЧМ-2013. -

Пенза, Изд-во ПГУ, 2013. С. 184-188.

3.Пантелеев И.Н., Пантелеев А.И. Моделирование аварийного разрушения сосудов с газом под давлением // Физико-математическое моделирование систем: материалы XIII Междунар. семинара. Воронеж: ФГБОУ ВО «Воронежский государственный технический универ-

ситет», 2015. Ч. 2. С. 123-128.

4.Пантелеев И.Н. Математическое моделирование экологического ущерба при выбросе загрязняющих веществ в атмосферу // Современные методы прикладной математики, теории управления и компьютерных технологий: сб. тр. IX междунар. конф. «ПМТУКТ2016». Воронеж: Изд-во «Научная книга», 2016. С. 261-264.

ANALYSIS OF SAFETY OF TECHNICAL OBJECTS

IN THE CONDITIONS OF RISK SITUATIONS

I.N. Panteleev

Voronezh State Technical University

Potentially possible impact on an object directed to violation of its safety is considered. The analysis of parameters of systems of protection of technical objects in the conditions of risk situations and threats is carried out. It is shown that the management of parameters of systems of protection of technical objects assumes minimization of the common risk of threats to security of an object; optimum choice of indexes of system of protection; decomposition of the common risk and its distribution on separate threats

Keywords: model operation and optimization, risk analysis

119