
3365
.pdf
где F , Fв , Fd соответствуют конструкционным и тепловым
0
деформациям в системе, массовым силам и распределенным нагрузкам.
Этот анализ может быть распространен на трехмерные фермы и случаи жестких соединений, когда силы и моменты передаются через узлы.
Пример
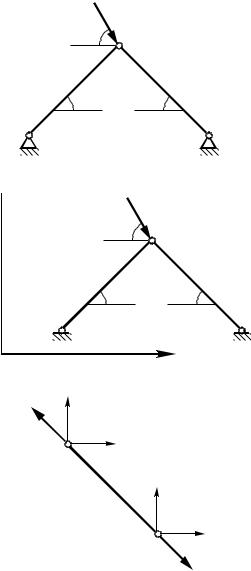
Для шарнирно-соединенной фермы (рис. 4.3) вычислить смещения в узле 2, предполагая, что каждый стержень имеет длину, равную 10 см и поперечное сечение равное 1 см2.
Модуль Юнга Е = 2 106 кг/см2.
Согласно уравнению (4.3), для элемента 1 сила, дейст-
вующая вдоль стержня, равна |
|
|
|
|
|
|||||||
|
EA1 |
|
|
|
|
|
|
|
|
|
(4.15) |
|
|
|
|
|
|
|
|
|
|||||
P |
|
|
|
x2 |
|
x1 cos135 |
|
y2 |
|
y1 sin135 , |
||
L1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
отсюда с помощью уравнений (4.4) и (4.6, а) получаем:
|
Fx1 |
P cos135 |
|
1 |
1 |
|
1 |
1 |
|
F e1 |
Fy |
|
P sin135 |
105 |
1 |
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
Fx |
2 |
P cos135 |
|
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Fу |
2 |
P sin135 |
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
x1
y1 . (4.16)
x2
y2
Для элемента 2 аналогично получаем соотношения:
|
EA2 |
|
|
|
|
|
|
|
|
|
, |
(4.17) |
|
|
|
|
|
|
|
|
|
||||||
P |
|
|
|
x2 |
|
x3 cos 45 |
|
y2 |
|
y3 sin 45 |
|||
L2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Fx3 |
P cos 45 |
|
1 |
1 |
|
1 |
1 |
|
x3 |
|
||
Fy |
|
P sin 45 |
|
1 |
1 |
|
1 |
1 |
|
y |
|
|
F e2 |
3 |
|
105 |
|
|
|
|
|
|
|
3 |
. (4.18) |
Fx |
2 |
P cos 45 |
|
|
1 |
1 |
1 |
1 |
|
x |
2 |
|
F |
|
P sin 45 |
|
|
1 |
1 |
1 |
1 |
|
y2 |
|
|
|
|
|
|
|
||||||||
у |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
79 |
|
|
|
|
|
|
|
|
|
60 o |
R2=1000 кг с |
|
2 |
||
|
||
e2 |
e |
|
|
1 |
|
45 o |
45 o |
|
3 |
1 |
|
|
а |
y 
3
0
_ |
_ |
|
Fy |
||
P |
||
2 |
||
|
||
|
2 |
|
R2=1000 кг с |
60 o |
2 |
|
|
e2 |
e1 |
45 o |
45 o |
1
б |
x |
|
|
|
|
_ |
|
|
Fx |
|
|
2 |
|
|
e1 |
_ |
|
|
Fy1 |
_ |
|
|
|
Fx |
|
1 |
1 |
|
_ |
||
|
||
|
P |
|
в |
|
Рис. 4.3
80
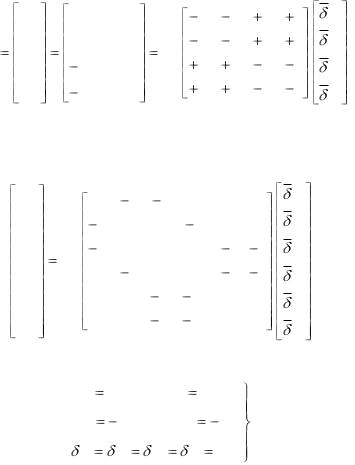
Для того чтобы проиллюстрировать процесс последовательного построения более четко, преобразуем уравнение (4.19) так, чтобы нумерация узлов в его матрицах подчинялась той же последовательности, что и в уравнении (4.17):
|
Fx2 |
P cos 45 |
|
1 |
1 |
1 |
1 |
|
F e2 |
Fy |
2 |
P sin 45 |
105 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
Fx |
|
P cos 45 |
|
1 |
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
Fу |
3 |
P sin 45 |
|
1 |
1 |
1 |
1 |
x2
y2 . (4.19)
x3
y3
Расширяя (4.17) и (4.20) до размерности системы и формируя результирующие уравнения поэлементным объединением согласно (4.11), получаем матричное уравнение:
Rx |
|
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
|||||||
|
|
|
|
|
|
|
||
Ry1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
|
Rx |
2 |
105 |
1 |
1 |
2 |
0 |
1 |
1 |
Ry |
2 |
|
1 |
1 |
0 |
2 |
1 |
1 |
|
|
|
|
|
|
|
|
|
Rx3 |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
Ry |
|
|
0 |
0 |
1 |
1 |
1 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как
x1
y1
x2 . (4.20)
y2
x3
y3
Rx2 |
1000cos 60 |
|
500 |
|
||||||
Ry |
2 |
|
1000sin 60 |
866 , |
(4.22) |
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
x1 |
|
y1 |
|
x3 |
x3 |
|
|||
то уравнение (4.21) можно записать в виде
81
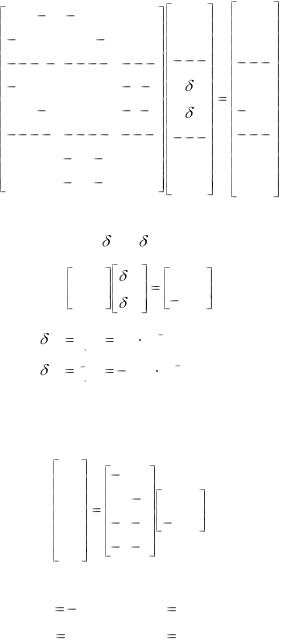
1 |
1 | |
|
1 |
|
|
|
1| 0 |
0 |
|
|
0 |
|
|
Rx |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||||||||
1 |
1| 1 |
|
|
|
1| 0 0 |
|
|
0 |
|
|
Ry |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
105 1 |
1| |
|
2 |
|
|
|
0 | |
|
1 |
1 |
|
|
|
|
x2 |
|
500 . |
(4.22) |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
1| |
0 |
|
|
|
2 | |
|
1 |
1 |
|
|
|
|
y2 |
|
860 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 0 | 1 |
|
1 | 1 1 |
|
|
0 |
|
|
Rx |
3 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 | 1 |
|
|
|
1 | 1 1 |
|
|
0 |
|
|
Ry |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
Разбиение матриц в (4.23), показанное штриховыми ли- |
|||||||||||||||||||||||||
ниями, позволяет найти |
|
|
|
х2 |
и |
|
у2 |
как решение системы |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
5 |
2 |
|
1 |
|
|
|
|
x2 |
|
|
|
|
500 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
10 |
0 |
|
2 |
|
|
|
|
y2 |
|
|
|
|
866 |
; |
|
|
(4.23) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
500 |
|
2,5 10 |
3 |
( см ); |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
т.е. |
|
|
|
2 10 |
5 |
|
|
|
|
|
(4.24) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
866 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
|
|
|
у2 |
|
|
|
|
|
|
|
4,33 10 |
( см ). |
|
|
|
||||||||||
|
|
|
|
2 10 |
5 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подстановка равенства (4.25) в (4.23) дает следующее |
|||||||||||||||||||||||||
выражение для реакций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Rx1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Ry |
1 |
|
|
|
|
|
|
|
1 |
1 |
|
250 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
433 , |
|
|
|
(4.25) |
||||
|
|
|
Rx3 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
||||||||||
|
|
|
Ry |
3 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rx |
|
683 кгс; |
Ry |
|
|
683 кгс; |
|
|
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
(4.26) |
||
|
Rx3 |
183 кгс; |
|
|
Ry3 |
|
|
183 кгс. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82 |
|
|
|
|
|
|
|
|
|
|
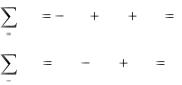
Эти результаты могут быть проверены путем использования условий равновесия фермы:
3 |
|
Rxi |
683 500 183 0; |
i 1 |
(4.28) |
|
3 |
||
|
Ryi 683 866 183 0.
i1
4.2.Дискретное моделирование разъемного соединения секций трубопровода с вакуумной изоляцией
для транспортировки криогенных продуктов
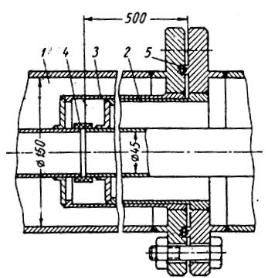
Длительно работающие трубопроводы для жидкого кислорода снабжают вакуумными видами изоляции. Трубопроводы с вакуумной изоляцией изготавливают в виде отдельных секций со своими вакуумными камерами. Для соединения секций трубопровода в конструкциях, где при разъеме возможно осевое перемещение, широко используется разъемное соединение, изображенное на рис. 4.4. Оно позволяет свести к минимуму приток тепла по металлу на концах секции, поддерживая уплотнение при температуре окружающей среды.
Проблема заключается в необходимости детального исследования напряженно-деформированного состояния конструкции соединения, обеспечивающей достаточную герметичность стыка. Использование аналитических методов не представляется возможным из-за сложности расчетной модели и характера нагружения конструкции.
Проектирование конструкции на современном уровне предусматривает использование численных методов исследования, среди которых наиболее развит метод конечных элементов.
Постановка задачи предусматривает исследование на- пряженно-деформированного состояния пространственной ли- нейно-упругой конструкции разъемного соединения секций трубопровода, статически нагруженной силами внешнего атмосферного давления, силами от давления транспортируемого
83
продукта и силами, возникающими от затяжки болтов фланцевого соединения.
Рис. 4.4. Конструктивная схема соединения
При построении конечно-элементной модели использованы объемные элементы в форме призмы с треугольным основанием, пластинчатые элементы треугольной и четырехугольной формы с узлами в вершинах. Узел объемного элемента имеет 3 степени свободы: линейные перемещения вдоль осей глобальной системы координат. Каждый узел пластинчатого элемента имеет 3 линейные степени свободы вдоль трех осей локальной системы отсчета и трех угловых степеней, соответствующих поворотам вокруг этих осей. Пластинчатый элемент испытывает суперпозицию плоского напряженного состояния и изгиба.
84
4.2.1. Конечные элементы, используемые для моделирования конструкции разъемного соединения трубопровода
4.2.1.1. Объемный элемент в форме прямой треугольной призмы (пентаэдр)
Рассматриваемый элемент (рис. 4.5) представляет собой прямую треугольную призму. Целесообразность применения такого рода элементов связана с тем, что:
многие детали имеют призматическую (цилиндрическую) форму или частично состоят из призматических подобластей;
при аппроксимации пентаэдрами подобных трехмерных областей существенно упрощается проблема автоматизи-
рованной подготовки данных, возникающая, в частности, в
случае использования тетраэдров.
а |
б |
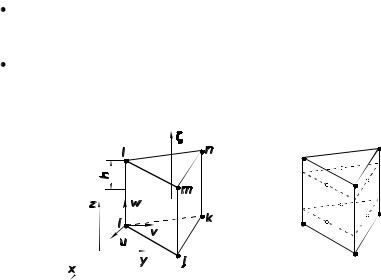
Рис. 4.5. Объемный элемент в форме прямой треугольной призмы:
а– геометрия, узлы и узловые перемещения;
б– расположение точек численного интегрирования
Простейший, первого порядка, пентаэдр (рис. 4.5) имеет узлы i, j, k, l, m, n, расположенные только в вершинах. Особенностью описываемого пентаэдра является то, что его нижнее и верхнее
основания параллельны плоскости xOy, а боковые ребра – оси z.
Принятый порядок локальной нумерации узлов указан на рис. 4.5: последовательность обхода узлов i, j, k нижнего треугольного основания принимается против хода часовой стрелки,
85
если смотреть со стороны верхнего основания, а узлы l, m, n располагаются соответственно над узлами i, j, k.
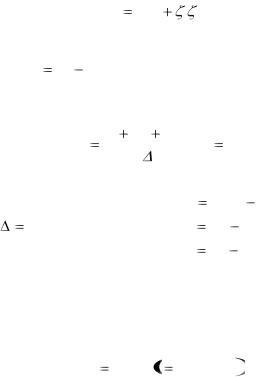
Функции форм прямого пентаэдра образуются путем умножения функции, интерполирующей перемещения точек в плоскости треугольного основания, на функцию, интерполирующую по третьей координате. Перемещения точек основания в его плоскости описываются с помощью L-координат, а для третьей координаты z применяется линейная интерполяция с применением функций
fi |
1 |
(1 |
i ) , |
(4.28) |
|
2 |
|||||
|
|
|
|
в которых индекс i обозначает номер узла, а безразмерная координата  ( z zc ) / h отсчитывается от точки C, в данном случае – от центра тяжести объема пентаэдра.
( z zc ) / h отсчитывается от точки C, в данном случае – от центра тяжести объема пентаэдра.
В рассматриваемом случае L-координаты имеют вид
|
|
|
|
Li |
|
ai |
bi x |
ci |
y |
( i |
|
1,2,3 ) , |
(4.29) |
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x1 |
y1 |
|
|
|
a1 |
|
x2 y3 |
|
|
x3 y2 ; |
|
||||||
|
1 |
|
|
|
|
|
|
|
|||||||||||
|
1 |
x |
|
y |
|
|
; |
|
b |
|
y |
|
y |
|
; |
|
|||
|
|
2 |
2 |
|
|
|
2 |
3 |
|
||||||||||
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
1 |
x3 |
y3 |
|
|
|
c1 |
|
x3 |
x2 |
|
|
|||||||
и остальные коэффициенты в (4.29) получаются циклической перестановкой индексов.
Функции форм прямого пентаэдра определяются как произведения функций (4.28) и (4.29):
Ni Li fi i 1,2,3,4,5,6 . |
(4.30) |
Интегрирование, предусмотренное для вычисления компонентов матрицы жесткости, может быть выполнено точно, однако с учетом общего численного характера конечноэлементного моделирования используется более простое и целесообразное в данном случае численное интегрирование.
86

Применяются квадратурные формулы типа Гаусса при расположении точек интегрирования в значениях весовых коэффициентов. Соответственно принятым функциям форм прямого пентаэдра интегрирование выполняется при расположении трех точек в каждом из двух сечений (рис. 4.5).
4.2.2. Пластинчатый элемент треугольной формы
Рассматриваемый элемент (рис. 4.6) применяется для моделирования тонких упругих пластин, находящихся в состоянии суперпозиции изгибного и плоского напряженного (мембранного) состояний. В последнем варианте такого рода элементы эффективно применяются для аппроксимации оболочек как совокупности плоских элементов.
а |
б |
в |
Рис. 4.6 Пластинчатый элемент в форме произвольного треугольника:
нумерация узлов и обозначения узловых перемещений
вмембранном (а), изгибном (б) состояниях
ипри их суперпозиции (в)
Узлы элемента i, j, k располагаются только в углах и нумеруются против хода часовой стрелки, если смотреть на пластинку с «лицевой» стороны.
Локальная матрица жесткости такого элемента при суперпозиции мембранного и изгибного состояний имеет блочную структуру из подматриц.
Изгибное состояние элемента описывается путем аппроксимации функции прогибов полиномом в L-координатах с девятью неопределенными коэффициентами 1, , 9 , число ко-
87
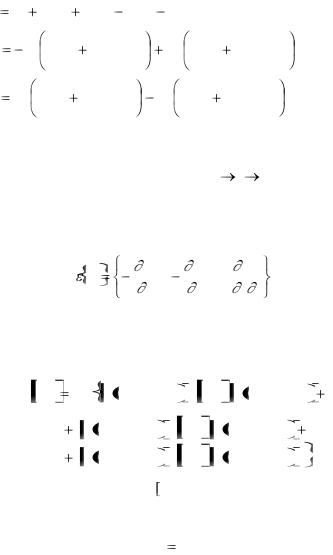
торых соответствует числу степеней свободы изгибаемого треугольного элемента. С учетом выбранного положительного направления узловых перемещений (рис. 4.6, б) функции формы, соответствующие первому узлу, имеют вид:
N L L2 L |
j |
L2 L L L2 |
L L2 ; |
|
|
|
|
|||||||||||||
1 |
i |
|
i |
|
|
|
|
i |
k |
i j |
|
i |
k |
|
|
|
|
|||
N |
|
|
y |
L2 L |
|
|
|
1 |
L L L |
y |
|
L2 L |
|
1 |
L L L ; |
(4.31) |
||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
ij |
i |
|
|
j |
|
|
2 |
|
i j k |
|
ki |
i k |
|
2 |
i j k |
|
N |
|
x |
|
L2 L |
|
|
|
1 |
|
L L L |
x L2 L |
1 |
L L L . |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 |
|
ji |
|
i |
j |
|
2 |
|
i |
j k |
ik |
|
i k |
2 |
|
i j k |
|
||
где yij = yi – yj; |
yki = yk – yi; |
xji |
= xj – xi; |
xik = xi – xk. |
|
|||||||||||||||
Функции форм для остальных узлов получаются циклической перестановкой индексов i j k.
На основе исходных зависимостей технической теории изгиба тонких упругих пластин для компонентов относительных деформаций
Џ |
2w |
, |
2w |
, 2 |
2w |
T |
|
|
|
|
|
. |
(4.32) |
||
|
x2 |
y2 |
x y |
Матрица жесткости в изгибном состоянии вычисляется с помощью численного интегрирования по формуле, дающей точный результат:
K И |
S |
B 0.5, 0.5, 0 |
T |
DИ B 0.5, 0.5, 0 |
|
|
|
||||
3 |
|
|
|||
|
|
|
|
|
|
|
B 0, 0.5, 0.5 T |
DИ |
B 0, 0.5, 0.5 |
(4.33) |
|
|
B 0.5, 0, 0.5 T DИ |
B 0.5, 0, 0.5 . |
|
||
Матрица упругости DИ изгибаемой пластины выражается через матрицу [D] в мембранном состоянии формулой
изгибаемой пластины выражается через матрицу [D] в мембранном состоянии формулой
[D И ] |
|
t3 |
|
[D] . |
(4.34) |
|
12 |
||||||
|
|
|
||||
|
88 |
|
||||
