3365

Величина фиктивного звена равна расстоянию между центрами кривизны элементов высшей пары.

О1О2 – фиктивное звено.

О1О2 = 1 2. Механизм AО1О2B является заменяющим.

1.8. Классификация плоских механизмов

Механизмы можно классифицировать по различным признакам.

1.Механизмы, в состав которых входят только низшие пары и, наоборот, высшие.

2.По конструктивным признакам: шарнирно-рычажные, зубчатые, кулачковые и др.

3.По характеру воспроизводимого движения: передающие вращательное, поступательное движения.

Можно привести ещѐ ряд классификаций. Однако наиболее общей из всех является классификация по АссуруАртоболевскому.

Прежде чем перейти к классификации, познакомимся с принципом образования механизмов. Впервые он сформулирован в 1914 году ученым Петербургского политехнического института Д.В. Ассуром и состоит в следующем: механизм создается путем последовательного наложения кинематических цепей, обладающих определенными структурными свойствами.

В этом определении дается основной принцип структур-

ного синтеза механизмов.

Структурным синтезом механизмов называется проек-

тирование структурной схемы механизма, под которой понимается схема механизма с указанной стойкой, подвижными звеньями, видами кинематических пар и их взаимным расположением.

Принцип создания механизма проследим на примере плоского механизма. Рассмотрим следующий механизм

(рис. 1.18).

В этом механизме одно начальное или ведущее звено –

АВ (звено 1); задана одна обобщенная координата , которая

19

определяет положение всех остальных звеньев относительно стойки. Звенья 2, 3, 4 и 5 – ведомые, стойка – 0. Как же образовался механизм?

n=5; P5=7; W=1.

Рис. 1.18

Вначале к ведущему звену 1 и стойке 0 присоединили группу звеньев 2 и 3, получили механизм шарнирного четырехзвенника АВСD: n=3, P5=4, W=1. Затем к звену 3 и стойке присоединили звенья 4 и 5, получили данный механизм ABCDE, W=1. После присоединения к начальному звену звеньев 2, 3, 4, 5 степень свободы механизма не изменилась, это значит, что кинематическая цепь из звеньев 2, 3, 4, 5 имеет степень свободы равную нулю.

Кинематическая цепь, обладающая нулевой степенью свободы после присоединения ее свободными элементами к стойке, называется структурной группой или группой Ассура. Такая группа не должна распадаться на более простые группы, обладающие нулевой степенью свободы.

Кинематическую цепь из звеньев 2, 3, 4 и 5 можно разделить на две структурные группы: первая из звеньев 2 и 3, вторая из звеньев 4 и 5 (рис. 1.19). Обе эти группы имеют W=0.

Кинематическая цепь из двух звеньев и трех кинематических пар является простейшей структурной группой. Такую группу называют группой II класса и 2 порядка.

20

2 C

n=2; P5=3; W=3 2–2 3=0.

Рис. 1.19

Структурная группа должна удовлетворять следующему условию:

W=3n–2P5=0; 3n=2P5; P5=(3/2) n.

В таблице дается сочетание звеньев и кинематических пар, из которых могут быть составлены структурные группы.

Первое сочетание n=2, P5=3 представлено группой второго класса. Такие группы имеют пять разновидностей.

Если группу второго класса присоединить к начальному звену и к стойке, получим механизм второго класса. Групп может быть сколько угодно, но это не меняет класс механизма.

Рассмотрим следующее сочетание: n=4, P5=6. Здесь возможны виды структурных групп, представленные на рис. 1.20.

Класс группы определяется классом замкнутого контура, входящего в группу. Класс контура определяется числом его сторон или числом кинематических пар в контуре. Порядок – число свободных пар контура. Представленная на рис. 1.20

21

первая группа будет III класса 3 порядка, а вторая IV класса 2 порядка.

Если в механизме есть группа III класса (не выше), то такой механизм будет механизмом III класса. Если ввести группу IV класса, то механизм будет IV класса.

Класс механизма определяется наивысшим классом группы, входящей в данный механизм. Рассмотренный механизм (рис. 1.20) состоит из двух групп второго класса, присоединенных к начальному звену и к стойке, значит, класс механизма второй. Начальное (ведущее) звено со стойкой есть механизм I класса. При структурном синтезе последовательно присоединяются структурные группы определенного класса к механизму I класса (начальному) и к стойке.

Для чего необходимо знать класс механизма? В зависи-

мости от класса механизма выбираются методы кинематического и силового исследования механизма.

Имея структурную схему механизма, всегда возможно определить класс механизма. Для этого из структурной схемы механизма необходимо выделить структурные группы определенного класса, выполняя нужную последовательность.

Рассмотрим определение класса механизма на примере (рис.

1.21).

1.Отсоединим от механизма самую простую по классу группу Асcура, наиболее удаленную от ведущего звена, с тем условием, чтобы оставшаяся цепь была механизмом и сохранила заданную степень свободы, т.е. W=1.

2.Отсоединив одну группу, определим ее класс и переходим к следующей.

22

W=3n–2Р5–Р4; n=7; Р5=10; W=1.

Рис. 1.21

В данном механизме можно выделить две группы (рис. 1.22): одна из звеньев 6 и 7 – II класса 2 порядка; вторая из звеньев 2, 3, 4 и 5 – III класса 3 порядка. Весь механизм будет III класса. Формула строения механизма представлена на рис. 1.22.

II(6,7) I (1,0) III(2,3,4,5)

Рис. 1.22

В этом же механизме изменим ведущее звено, выберем ведущим звено ЕF и определим снова класс механизма. Он изменится на второй, значит, класс механизма зависит от выбора ведущего звена.

23

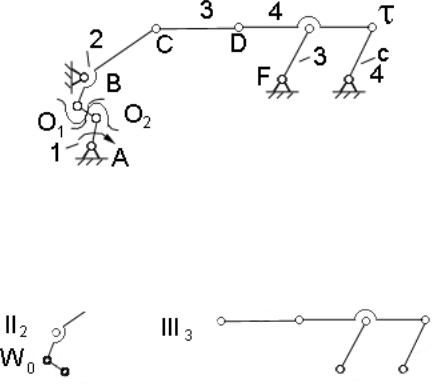
Рассмотрим механизм, в состав которого входит высшая кинематическая пара. Пару составляют звено 1 и 2 (рис. 1.23).

Рис. 1.23

Прежде чем определить класс механизма, необходимо произвести замену высшей пары. Правило замены известно. Строим заменяющий механизм и определяем его класс (рис. 1.24). В механизм входят две группы: второго и третьего класса.

Рис. 1.24

Следовательно, исходный (заданный) механизм также третьего класса. Классификация по Ассуру-Артоболевскому дана только для плоских механизмов.

1.9. Структурные группы пространственных механизмов

Принцип образования механизмов является общим для плоских и пространственных. Условие существования пространственных структурных групп то же, т.е. W=0.

Степень свободы определяется выражением

24

W=6n-5Р5–4Р4–3Р3–2Р2–Р1.

Пусть пространственный механизм состоит из звеньев, соединенных парами только 5-го класса (рис. 1.25). Структурная формула для него имеет вид W=6n-5Р5. Условие существования групп: Wгр. = 0, т.е. 6n=5Р5. Структурная группа будет выглядеть так: n = 5; 5Р5=6n; W=0.

Рис. 1.25

Структурная группа получается громоздкой. Выберем другой состав звеньев и пар в механизме (рис. 1.26).

Рис. 1.26

W=6n–5Р5–4Р4–3Р3

Условие существования группы: Wгр. = 0

6n=5Р5+4Р4+3Р3

В этом случае n=2; Р5=1; Р4=1; Р3=1

Если такую группу присоединим к начальному звену, движение которого определяет одна обобщенная координата,

25

получим пространственный механизм со степенью свободы, равной единице (рис. 1.27)

n=3;Р5=2; Р4=1; Р3=1; W=6 3–5 2–4 1–3 1–1.

Рис. 1.27

Следовательно, принцип образования пространственных механизмов сохраняется.

2.АНАЛИЗ МЕХАНИЗМОВ

2.1.Кинематический анализ механизмов

Кинематический анализ механизмов – это изучение движения звеньев механизма без учета сил, вызывающих движение. Определяющим фактором здесь является степень свободы механизма. Закон движения ведущих (начальных) звеньев известен, поэтому можно сказать, что кинематический анализ состоит в определении движения звеньев механизма по заданному движению начальных звеньев.

Основные задачи кинематического анализа следующие:

1)определение положений звеньев, включая определение траектории движения отдельных точек;

2)определение передаточных функций, скоростей и ускорений звеньев механизма.

26

Методы кинематического анализа:

1)аналитические;

2)графоаналитические;

3)графические;

4)экспериментальные.

В настоящее время аналитические методы анализа выходят на первое место, чему способствует развитие ЭВМ. Однако графоаналитические и графические методы хотя и уступают в точности получаемых результатов, широко распространены изза своей наглядности и доступности.

Ниже рассмотрено аналитическое решение задачи о положениях звеньев механизма по методу преобразования координат. Метод предложен Ю.Ф. Морошкиным.

2.1.1. Определение положений звеньев плоской незамкнутой кинематической цепи

Также кинематические цепи лежат в основе манипуляторов. Рассмотрим четырехзвенную незамкнутую цепь только с вращательными парами 5-го класса, оси кинематических пар параллельны, т.е. цепь плоская (рис. 2.1). Определим степень свободы кинематической цепи.

n=3; Р5=3; W=6 3–2 3=3.

Рис. 2.1

27