
Полярная система координат. Параметрически заданные кривые. Приложения определенного интеграла. Каверина В.К., Некрасова Н.Н
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВО «Воронежский государственный технический университет»
В.К. Каверина Н.Н. Некрасова Л.В. Акчурина
ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ. ПАРАМЕТРИЧЕСКИ ЗАДАННЫЕ КРИВЫЕ. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Утверждено учебно-методическим советом университета в качестве учебного пособия
Воронеж 2018
УДК 517.98.74 ББК 22.161.6я7
К125
Рецензенты:
кафедра цифровых технологий Воронежского
государственного университета (д-р физ.-мат. наук,
проф., зав. кафедрой С.Д. Куралгин); д-р техн. наук, проф., зав. кафедрой «Информатики
и графики» Воронежского государственного технического университета В.П. Авдеев
Каверина, В.К.
Полярная система координат. Параметрически заданные кривые. Приложения определенного интеграла: учеб. пособие [Электронный
ресурс]. – Электрон. текстовые и граф. данные (2,5 Мб) / В.К. Каве- К125 рина, Н.Н. Некрасова, Л.В. Акчурина. – Воронеж: ФГБОУ ВО
«Воронежский государственный технический университет», 2018.
– 1 электрон. опт. диск (CD-ROM): цв. – Систем. требования: ПК 500 и
выше; 256 Мб ОЗУ; Windows XP; SVGA с разрешением 1024x768;
Adobe Acrobat; CD-ROM дисковод; мышь. – Загл. с экрана.
ISBN 978-5-7731-0642-5
Учебное пособие содержит основные сведения по полярной системе координат, методам построения в ней плоских кривых. Кроме того, в нем рассматриваются функции, заданные параметрическим образом. Рассмотрено большое число примеров построения кривых, используемых при изучении инженерностроительных дисциплин. В пособии даны задачи для самостоятельного решения.
Предназначено для студентов первого курса академического бакалавриата очной и заочной форм обучения.
Табл. 9. Ил. 59. Библиогр.: 14 назв.
|
УДК 517.98.74 |
|
ББК 22.161.6я7 |
ISBN 978-5-7731-0642-5 |
© Каверина В.К., Некрасова Н.Н., |
|
Акчурина Л.В., 2018 |
|
© ФГБОУ ВО «Воронежский |
|
государственный технический |
|
университет», 2018 |
2
ВВЕДЕНИЕ
Кривые с древних времён привлекали к себе внимание учёных и использовались ими для описания различных природных явлений от траектории брошенного камня до орбит космических тел. В практической и исследовательской работе инженерно-технических специалистов графическое изображение функций – это необходимый элемент. Поэтому, несмотря на наличие современных специализированных программных средств, студенты должны хорошо владеть техникой построения графиков различных функций.
Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами. Способ задания начальных условий для решения какой-нибудь конкретной технической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений и построения графиков функций часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат.
В настоящем пособии рассматриваются различные классы функций и методы построения их графиков в полярной системе координат, а также заданные параметрическим образом. Для некоторых кривых, которые не были изучены ранее, приводятся выводы их уравнений, чтобы избежать громоздких выкладок. А именно, изложение понятия более сложной кривой строится из логической последовательности действий, позволяющей ее осмыслить студентами и представить изучаемую кривую на уровне, достаточном для приложений.
Знакомство студентов с кривыми происходит в первом семестре при изучении раздела математики «Аналитическая геометрия». Разделу математического анализа, связанному с описанием кривых в различных системах координат, традиционно отводится в читаемых курсах лекций второстепенная роль. В то же время во многих прикладных и инженерных вопросах часто удобно задавать кривые в полярной системе координат или параметрическим образом. Поэтому данное пособие преследует цель помочь студентам систематизировать и укрепить свои знания в области представления кривых, широко используемых в различных областях инженерных знаний. Пособие послужит справочным материалом для воспроизведения изученных кривых и ознакомления с новыми кривыми, необходимыми для применения в разделах математического анализа. В первую очередь оно будет полезным при изучении тем: «Аналитическая геометрия на плоскости», «Приложение определенных и кратных интегралов к задачам геометрии и механики».
Приведенные краткие теоретические сведения, задания для самостоятельного решения и примеры по каждому разделу позволят студенту технических специальностей увидеть разнообразие конкретных форм изучаемого объекта и дадут возможность углубить свои знания. Структура пособия достаточно полно характеризуется содержанием.
3
ГЛАВА 1. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
1.1. Основные понятия
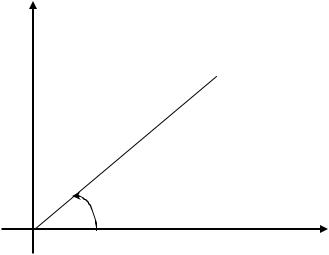
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую ОХ, называемую полярной осью (рис. 1.1). Пусть М – произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ, равным . Расстояние точки
М от полюса называется полярным радиусом точки М, а угол ХОМ , отсчитываемый от полярной оси к отрезку ОМ против движения часовой стрелки, – полярным углом. Полярный радиус и полярный угол составляют полярные координаты точки М. Точка М с полярными координатами, и записывается следующим образом: М ( , ) .
Y
|
|
M ( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
A |
Х |
|
Рис. 1.1. Полярные координаты точки на плоскости
Что касается значений, принимаемых полярными координатами, то достаточно рассматривать значения 0 ≤ p < +∞ и 0 ≤ φ < 2π, при этом угол φ, как было указано ранее, отсчитывается от полярной оси против хода часовой стрелки. В некоторых задачах приходится рассматривать углы больше, чем 2 , а также отрицательные углы, т.е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки. Если принимает отрицательное значение, то его
длина откладывается не по лучу, а по его противоположному продолжению. При 0 полу-
чим точку, совпадающую с полюсом О.
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат XOY, а полярная ось совпадает с положительным направлением оси OX (см. рис.
1.1). Тогда для произвольной точки М имеем: OA x ; AM y ; |
OM ; ХОМ . |
|
Считая угол острым, из прямоугольного треугольника AOM находим: |
||
OA OM cos ; |
AM OM sin , или |
|
x cos ; |
y sin . |
(1.1) |
Полученные формулы справедливы для любого угла |
и позволяют выразить прямо- |
|
угольные координаты точки М через ее полярные координаты. С другой стороны, из этого же прямоугольного треугольника AOM получаем
4
OM |
OA2 AM 2 ; |
tg |
AM |
; cos |
|
x |
; |
sin |
|
y |
|
, то есть |
||||||
|
|
|
|
|
||||||||||||||
|
|
|
OA |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x2 |
y 2 ; |
|
tg |
y |
; |
|
(1.2) |
|||||
|
|
|
|
|
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
cos |
|
x |
; |
|
sin |
|
y |
|
. |
(1.3) |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x2 y 2 |
|
|
|
|
|
|
x2 y 2 |
|
||||||
Формулы (1.2) и (1.3) выражают полярные координаты точки через ее прямоугольные ко- |
||||||||||||||||||
ординаты. Отметим, что при определении полярного угла |
из |
tg необходимо учитывать |
||||||||||||||||
знаки координат x и y .
Рассмотрим несколько примеров, которые в дальнейшем помогут строить кривые в полярных координатах.
Пример 1.1. Построить точки, заданные в полярной системе координат:
A(3, ) ; |
B(2, |
5 |
) ; |
|
C(3, ) ; |
D(3, ) ; E( 2, ) |
; |
|
F (3, ) . |
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
2 |
4 |
|
|
|
|
6 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
Решение. На рис. 1.2 изображены точки A(3, |
) ; |
B(2, |
5 |
) ; C(3, |
) ; |
D(3, |
) ; E( 2, ) ; |
||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
6 |
|
2 |
|||
F (3, ) . Поясним построение этих точек. Выберем полярную систему координат, т.е. проведем |
|||||||||||||||||||||||||||
полупрямую O из точки О, определим масштаб (единицу измерения длины) и положительное |
|||||||||||||||||||||||||||
вращение полярной оси (против хода часовой стрелки). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(3, |
) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (3, ) |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
E( 2, ) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
B(2, |
) |
|
|
|
|
|
|
|
2 |
|
|
|
C(3, |
) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(3, ) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Рис. 1.2. Точки в полярной системе координат
5
Тогда для построения точки A(3, |
) |
повернем полярную ось на угол |
|
против движе- |
|
2 |
|
2 |
|
ния часовой стрелки, а затем отложим от полюса в положительном направлении отрезок ОА, |
||||||||||||||||||||||||||||
равный по длине трем единицам. Концом этого отрезка и будет точка A(3, ) . |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Для построения точки B(2, |
5 |
) |
полярную ось поворачиваем на угол |
5 |
против хода |
|||||||||||||||||||||||
|
4 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
часовой стрелки, а затем откладываем от полюса |
в положительном направлении отрезок ОВ, |
|||||||||||||||||||||||||||
равный по длине двум единицам выбранного масштаба. Аналогично строим точку F (3, ) . |
||||||||||||||||||||||||||||
Для построения точки C(3, ) |
полярную ось нужно поворачивать в отрицательном на- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
правлении, |
т.е. по направлению движения часовой стрелки на угол, затем на ней отложить от- |
|||||||||||||||||||||||||||
резок ОС, равный по длине трем единицам масштаба. Аналогично строим точку D(3, ) . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
При построении точки |
E( 2, ) |
полярную ось поворачиваем на угол |
против хода |
|||||||||||||||||||||||||
часовой стрелки, |
и так как 2 , откладываем отрезок ОЕ, |
равный по длине двум единицам |
||||||||||||||||||||||||||
не на луче, соответствующем углу , а на его продолжении за полюс, т.е. на самой оси O . |
||||||||||||||||||||||||||||
Пример 1.2. В полярной системе координат даны точки |
|
M1 (4, ) ; |
M 2 (3, |
) ; |
M3 (6, ) . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
|
6 |
|
Найти их декартовы координаты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. Используем формулы (1.1) для нахождения декартовых координат по заданным |
||||||||||||||||||||||||||||
полярным координатам и . Так, для точки M |
|
(4, ) |
|
имеем x 4 cos 4 |
|
2 |
2 2 ; |
|||||||||||||||||||||
1 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y 4 sin |
4 |
|
2 |
2 2 , а значит, |
декартовы координаты точки M1 будут x 2 |
2 ; y 2 2 |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или M1 (2 |
2, 2 2 ) . Для точки M2 (3, |
) , как нетрудно видеть, |
x 3 cos |
0 ; |
y 3 sin 3 , |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
||
то есть в декартовых координатах M |
2 |
(0, 3) . Для точки |
M |
3 |
(6, ) по аналогии будем иметь: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
x |
6 cos |
|
|
6 |
|
|
3 3 |
; |
|
y 6 sin |
|
|
|
6 |
|
|
3 , |
M3 (3 3, |
3). |
|||||||||
6 |
|
2 |
|
|
|
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|||||||
На рис. 1.3 точки M1 , |
M 2 , M 3 |
изображены в декартовой и полярной системах координат. |
||||||||||||||||||||||||||
Точки на плоскости занимают одно и то же положение, в какой бы системе координат их не строить. Аналогично и кривая, построенная в декартовой и в полярной системах координат, не изменит своего положения на плоскости, в какой бы системе координат ее не строили. Поэтому построение линии проводят в той системе координат, где их уравнения проще.
Пример 1.3. Определить полярные координаты точек M1( 1, |
0) ; |
M2 ( 1, 1) . |
||||
Решение. |
Воспользуемся формулами (1.2). При нахождении угла , следует учитывать, |
|||||
в какой четверти находится точка M (x, y) . Для точки M1( 1, 0) имеем: |
x 1, |
y 0 и, сле- |
||||
довательно, |
( 1)2 02 1, tg |
0 |
0 . Так как x 1 0 , |
то точка M1 |
находится на |
|
|
||||||
|
|
1 |
|
|
|
|
6
оси O (рис. 1.4) |
и , следовательно, |
M1 в полярной системе координат имеет коорди- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
наты M (1, ) . Для точки |
M |
2 |
( 1, 1) при |
|
x 1 |
|
и |
|
|
|
y 1 |
|
|
( 1)2 ( 1)2 2 , |
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 1, а так как |
x 1 0 , |
y 1 0 , то |
|
5 |
. Тогда легко определяются поляр- |
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|||||
ные координаты точки M |
|
: |
|
2 , |
5 |
|
или |
|
|
|
|
|
|
|
5 |
) . |
|
|
|
|
|||||||||||
2 |
|
M |
2 |
( |
|
2, |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
M2 (0,3) |
|
|
|
M1(2 2,2 2) |
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
2 |
3 |
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
M3 |
(3 |
3, 3) |
|
Рис. 1.3. Точки в декартовой и полярной системах координат
Y
5
4
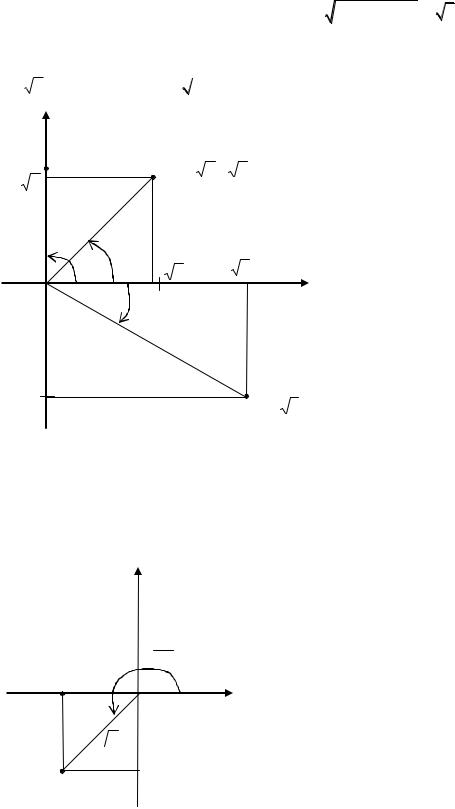
M1( 1,0)
0 |
X, |
 2
2
M2 ( 1, 1) |
Рис. 1.4. Геометрические представления к определению полярных координат точек
7
Пример 1.4. На рис. 1.5 изображен квадрат со стороной a 4 ед. Определить полярные координаты и вершин квадрата и середин его сторон.
Решение. Исходя из положения точек A, M, D, Q, C, R, B, N, O, нетрудно определить их декартовые координаты. Далее, если точку O считать полюсом, а ось O совместить с осью
OХ , то легко определить при выбранной масштабной единице полярные координаты этих точек. Студенту рекомендуется сделать это самостоятельно.
|
) ; B(2 |
|
|
|
3 |
|
|
|
|
5 |
|
|
|
|
7 |
) ; M (2, 0) |
|
||||
Ответ: A(2 2, |
2, |
|
) ; C(2 2, |
|
) ; |
D(2 2, |
; |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
4 |
|
|
4 |
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
||
|
|
|
|
|
|
|
|
N (2, |
) ; |
R(2, ) ; Q(2, |
3 |
) . |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
B |
|
|
|
|
|
N |
|
|
|
|
|
A |
|
||
|
|
M |
R |
0 |
2 X, |
C 
 Q
Q  D
D
Рис. 1.5. К определению декартовых и полярных координат вершин и середин сторон квадрата
Задачи и упражнения для самостоятельной работы
1.1. Построить точки, заданные полярными координатами A(2; π/4), B(3; 4π/3 ), C(1; π/6 ),
D(3; − 4π/3 ), E(4; − π/4 ).
1.2. Найти полярные координаты точек, заданных в декартовых координатах A(1;  3 ), B( 2
3 ), B( 2 3 ; 2), C(−4; 4), D(
3 ; 2), C(−4; 4), D(  2 ;
2 ;  6 ), если полюс совпадает с началом координат, а полярная ось
6 ), если полюс совпадает с началом координат, а полярная ось
сположительным направлением оси OХ.
1.3.Найти прямоугольные координаты точек, заданных в полярных координатах A( 2 2 ; 3π/4), B(7; π/2), C(3; 5π/4), D(1; − π/4), если полюс совпадает с началом координат, а полярная ось с положительным направлением оси OХ.
2 ; 3π/4), B(7; π/2), C(3; 5π/4), D(1; − π/4), если полюс совпадает с началом координат, а полярная ось с положительным направлением оси OХ.
1.4. Найти полярные координаты точек, симметричных точкам |
A(3; π/6), B(5; 2π/3), |
C(2; − π/6) относительно: 1) полюса; 2) полярной оси. |
|
8
1.2. Полярные уравнения линии
При исследовании формы линии на основании ее уравнения приходится часто пользоваться полярными координатами. Это удобно делать в том случае, если уравнение линии в полярных координатах проще, чем в декартовых. Иногда встречается надобность в переходе от уравнения линии в декартовых координатах к уравнению той же линии в полярных координатах, или наоборот. В этих случаях следует применять формулы (1.1), (1.2), (1.3), связывающие полярные и декартовы координаты.
В полярных координатах линия задается уравнением G( , ) 0 , связывающим полярные координаты ее текущей точки. Если возможно, то это уравнение разрешают относительно , и тогда уравнение линии в полярных координатах принимает вид ( ) . Если ( ) – непериодическая функция, то углу обычно придают как можно больше значений из области определения этой функции. Если функция периодическая, то значения функции находят, придавая углу значения, ограничиваясь изменением его в пределах первого периода для данной функции. При дальнейшем изменении значений угла полученные данные для значений исполь-
зуются в силу периодичности при построении всего графика функции.
Приведем примеры наиболее часто встречающихся линий, графики функций которых построены в полярной системе координат.
Пример 1.5. Найти полярное уравнение прямой x 1.
Решение. Используя формулу x cos , находим, что для данной прямой полярные ко-
|
1 |
|
|
ординаты связаны условием 1 cos |
или |
|
– это и есть уравнение данной прямой |
cos |
|||
(рис. 1.6). Поскольку – величина положительная, угол должен меняться так, чтобы cos оставался положительным, т.е. был в I и IV четвертях.
Y |
|
|
M ( , ) |
|
|
|
|
0 |
X, |
x 1
Рис. 1.6. Прямая x 1 в полярной системе координат
Пример 1.6. Найти полярное уравнение прямой, не проходящей через начало координат.
Решение. Рассмотрим нормальное уравнение прямой L:
x cos y sin p 0 ,
9
где |
p – расстояние от начала координат до прямой, – угол между осью OX и осью p (рис. |
1.7). |
|
|
Заменяя x и y по формулам (1.1), получим |
|
cos cos sin sin p 0 , |
т.е. |
cos( ) p . По условию, искомая прямая не проходит через начало координат, поэто- |
му отклонение |
p 0 . Разделив последнее равенство на cos( ) 0 , получим полярное урав- |
||
нение данной прямой в виде |
|||
|
|
p |
|
|
|
. |
|
|
cos( ) |
||
Нормальное уравнение прямой в полярной системе координат может быть получено и не- |
|||
посредственно |
из следующих соображений. Выберем на прямой L произвольную точку |
||
M ( , ) . Тогда проекция вектора OM на нормальный вектор Прn OM cos( ) const p , или
Y
M ( , )
p
n
0
n будет вычисляться по формуле
p . cos( )
X,
Рис. 1.7. К выводу нормального уравнения прямой в полярных координатах
|
Итак, уравнение прямой в полярной системе координат имеет вид |
p |
. При |
||
|
|
||||
|
cos( ) |
||||
0 |
получаем |
p |
, т.е. полярное уравнение прямой, перпендикулярной полярной оси |
||
|
|||||
cos |
|||||
(ее уравнение в декартовой системе координат x p ).
Пример 1.7. Пусть Г – эллипс, или ветвь гиперболы или параболы; F – фокус этой кривой; D – соответствующая директриса. Требуется определить уравнение кривой Г в полярной системе координат.
Решение. Уравнениями эллипса, гиперболы и параболы часто пользуются во многих задачах геометрии и механики. Получим эти уравнения в полярных координатах. Пусть O –
полярная полуось. Начало полярной системы координат поместим в фокус F (левый – в случае эллипса, правый – в случае гиперболы и единственный фокус параболы). На рис. 1.8 изображена
10
