
3007
.pdf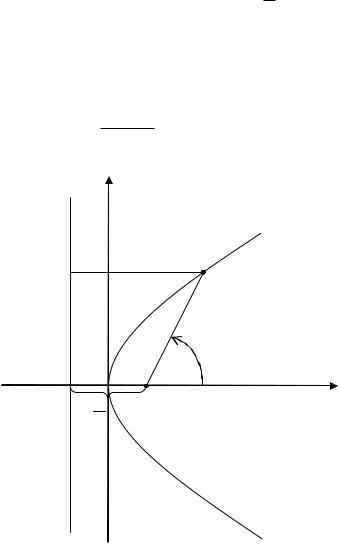
парабола. Полярная ось направлена в сторону, противоположную от соответствующей дирек-
p
трисы D. Обозначим расстояние от фокуса до директрисы через , где p – параметр кривой,
называемый полуфокальным диаметром.
Общее свойство эллипса, гиперболы и параболы состоит в следующем: для любой точки M отношение расстояния от точки М до фокуса F к расстоянию от точки М до директрисы есть величина постоянная:
r(M , F ) const. r(M , D)
Y
D
M
0
p F
(1.4)
X,
Г
Рис. 1.8. К выводу уравнений кривых второго порядка в полярной системе координат
Из рис. 1.8 следует, что r(M , F ) и r(M , D) |
p |
cos . Подставляя эти выражения в |
|||||||
|
|||||||||
|
|
|
|
|
|
|
|
||
(1.4), получаем |
|
|
|
, откуда окончательно |
|
|
|||
|
|
|
|
|
|||||
|
p |
cos |
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
p |
|
|
||
|
|
|
|
|
. |
|
(1.5) |
||
|
|
|
|
1 cos |
|
||||
Уравнение (1.5) и есть искомое уравнение в полярной системе координат, общее для эллипса, гиперболы и параболы, причем, если
1, то кривая, определяемая уравнением (1.5) – эллипс;
1 , то кривая (1.5) – гипербола;
1 , то кривая (1.5) – парабола.
11
Величина p |
b2 |
– фокальный параметр для эллипса и гиперболы. Для параболы |
p име- |
|
|||
|
a |
|
|
ет тот же смысл, что и в уравнении в декартовой системе координат y2 2 px (то есть |
p – рас- |
||
стояние от фокуса до директрисы). |
|
||
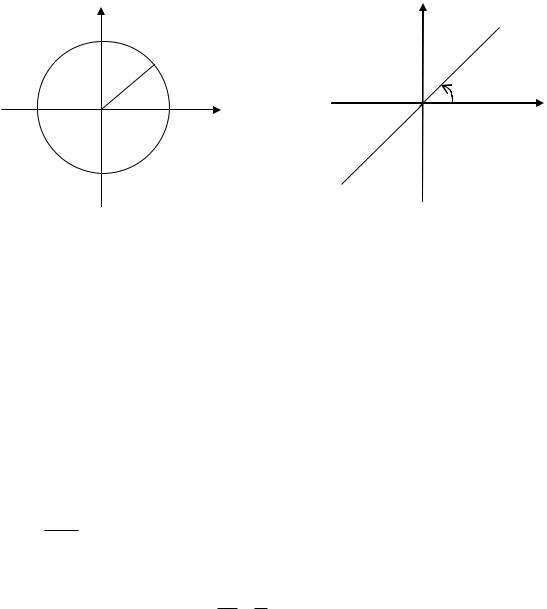
Пример 1.8. Что представляют собой линии, заданные в полярной системе координат уравнениям a const и const?
Решение. Геометрическое место точек, для которых – расстояние до полюса постоянно, есть окружность. Поэтому уравнение a определяет окружность радиуса a с центром в по-
люс О (рис. 1.9, а). |
|
|
|
|
а) |
|
|
б) |
|
Y |
|
|
Y |
|
|
|
|
|
|
a |
|
|
|
|
|
a |
a |
|
|
|
|
|
X, |
|
0 |
|
X, |
0 |
|
|
|
Рис. 1.9. Геометрические места точек, определяемые уравнениями:
а) a const; |
б) const |
Уравнению удовлетворяют все точки |
полупрямой, проведенной из полюса под уг- |
лом к полярной оси. Вся прямая, проходящая через полюс, записывается в полярной системе координат уравнениями и (рис. 9, б).
Пример 1.9. Даны прямая l и точка O, не лежащая на ней. Определить геометрическое место точек M, для которых OM OA C ( C 0 ), где A – произвольная точка прямой l.
Решение. Уравнение искомого геометрического места точек удобно записать в полярной системе координат, выбирая ее так, чтобы полюс был в точке O, а полярная ось O проходила
перпендикулярно данной прямой l.
Пусть ON p (рис. 1.10). Если использовать формулу
p |
|
то получим cos |
. Следовательно, полярный радиус точки |
x cos , то есть |
p cos , |
|||
A будет A |
|
p |
. |
|
|
||||
cos |
||||
|
|
|
||
Пусть ( , ) – полярные координаты точки M. По условию задачи A C , отсюда
C C cos 2R cos ,
A p
12
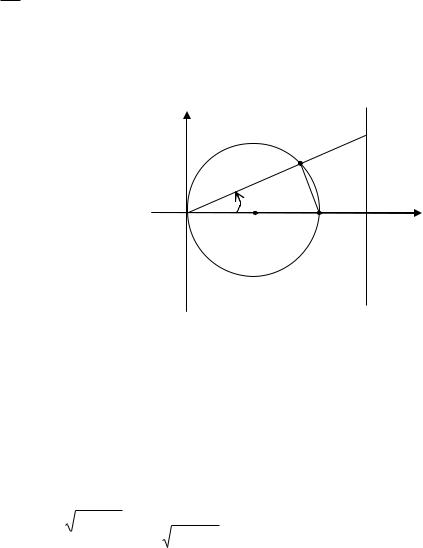
где R 2Cp . Таким образом, полярное уравнение геометрического места точек M имеет вид
2R cos .
l
Y
M ( , ) A
S Q
0 |
R |
2R N X, |
Рис. 1.10. Геометрические построения к примеру 1.9 по нахождению геометрического места точек
Это уравнение показывает, что в треугольнике OMQ угол QMO прямой и, как известно из элементарной геометрии, точка M расположена на окружности с диаметром OQ.
Тот же результат можно получить, |
если уравнение 2R cos преобразовать к декарто- |
||||||||
вым координатам, то есть |
|
|
|
|
|
|
|
||
|
|
x2 y2 |
2R |
|
x |
, |
или |
x2 y2 2Rx , |
или x R 2 y2 R2 . |
|
|
x2 |
y2 |
||||||
|
|
|
|
|
|
|
|
||
Последнее уравнение определяет окружность радиуса R с центром S(R,0). |
|||||||||
Пример 1.10. Записать уравнение окружности x2 y2 |
2ay в полярной системе коорди- |
||||||||
нат. |
|
|
|
|
|
|
|
|
|
Решение. Используя формулы (1.1), преобразуем уравнение x2 y2 2ay к виду |
|||||||||
|
|
|
|
|
2 cos2 2 sin 2 2a sin . |
||||
Значит, |
2 2a sin и окончательно |
|
|
||||||
|
|
|
|
|
|
2a sin . |
(1.6) |
||
Уравнение (1.6) есть уравнение окружности с центром C(O,a) и радиусом R=a. Действи- |
|||||||||
тельно, |
если |
выделить |
полный |
квадрат |
в уравнение |
x2 y2 2ay , то будем иметь |
|||
x2 y2 |
2ay a2 a2 , или x2 y a 2 |
a2 , что является уравнением окружности c центром в |
|||||||
точке C(O,a) и радиусом R=a.
13

Y
2a
2a sin
 С(0, a)
С(0, a)
0 |
X, |
Рис. 1.11. Окружность, проходящая через начало координат
Задачи и упражнения для самостоятельной работы
1.5.В полярной системе координат изобразить линии 3 / 4 , 2 / 3 .
1.6.Записать уравнение кривой x2 y2 6y в полярной системе координат и построить
кривую.
1.7.Записать уравнение кривой x2 y2 4x в полярной системе координат и построить
кривую.
1.8.В полярной системе координат написать уравнение окружности с радиусом 2, если: а) центр окружности находится в полюсе; б) полюс лежит на окружности, а полярная ось проходит через центр окружности.
1.3. Кривые, полярные уравнения которых содержат тригонометрические функции
1.3.1. Розы
Розами называют семейства кривых, полярные уравнения которых записываются в виде
a sin k |
или в виде a cos k , где a и k – положительные постоянные, k Z . Так как |
||||||
|
sin k |
|
1 и |
|
cos k |
|
1, то каждая кривая расположена внутри круга радиуса a. В силу того, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
что sin k и cosk – периодические функции, роза состоит из одинаковых частей (лепестков), симметричных относительно наибольших радиусов, каждые из которых равен a. Если k – це-
лое число, то роза состоит из 2k лепестков при k – четном, и из k лепестков при k – нечетном. При построении линии в полярной системе координат, если наблюдается симметрия отно-
сительно полярной оси, удобно сначала заготовить так называемую полярную сетку. Эта сетка строится из лучей, которые с полярной осью составляют углы, указанные в таблице значений
аргумента , окружностей с радиусами . Далее строят точки, координаты которых указыва-
ются в таблице, а также им симметричные. Кроме того, при построении кривых, уравнения которых содержат тригонометрические функции, следует учитывать период функции и использовать симметрию кривой относительно осей координат.
Пример 1.11. Построить кривую, заданную уравнением
14
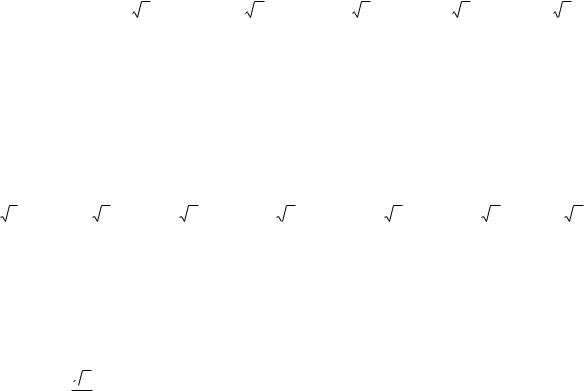
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.7) |
||||||||||||||||
|
|
|
|
Решение. Функция ( ) cos3 |
– периодическая, |
|
ее период равен |
|
|
|
2 |
, |
поэтому доста- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
точно определить значения функции ( ) cos3 в интервале от 0 |
|
до |
|
|
2 |
|
, остальные значения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
будут периодически повторяться. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
Найдем |
|
точки, |
лежащие |
на линии cos3 , |
|
|
придавая |
|
|
значения, |
|
равные |
|
|
|
k |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
12 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( k 0, 1, 2, 3, ... , 24 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Таблица значений функции составлена для от 0 |
до 2 |
через |
|
|
, |
|
|
что соответствует уг- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
лу в 150, то есть, весь круг разбивается на 24 сектора (табл. 1.1). |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полярные координаты кривой cos3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
2 |
|
|
|
3 |
|
|
|
5 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
6 |
|
|
4 |
|
|
|
|
3 |
|
|
12 |
|
|
|
|
|
2 |
|
|
|
|
12 |
|
|
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
6 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
3 |
|
|
|
|
|
7 |
|
|
|
|
|
2 |
|
|
9 |
|
|
5 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
cos3 |
|
1 |
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
-1 |
|
|
2 |
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
0 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
13 |
|
7 |
|
|
|
|
5 |
|
|
|
|
4 |
|
|
|
17 |
|
3 |
|
|
19 |
|
|
5 |
|
|
|
|
7 |
|
|
|
11 |
|
|
|
|
23 |
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
12 |
|
|
|
|
|
|
12 |
|
|
|
6 |
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
|
12 |
|
|
|
2 |
|
|
|
|
|
12 |
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
6 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
11 |
|
|
|
3 |
|
13 |
|
7 |
|
15 |
|
|
|
|
4 |
|
|
|
17 |
|
9 |
|
|
19 |
|
|
5 |
|
|
|
|
21 |
|
|
|
11 |
|
|
|
|
23 |
|
6 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
-1 |
|
2 |
|
|
0 |
|
|
|
2 |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
-1 |
|
|
|
|
2 |
0 |
|
|
|
|
2 |
|
|
1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
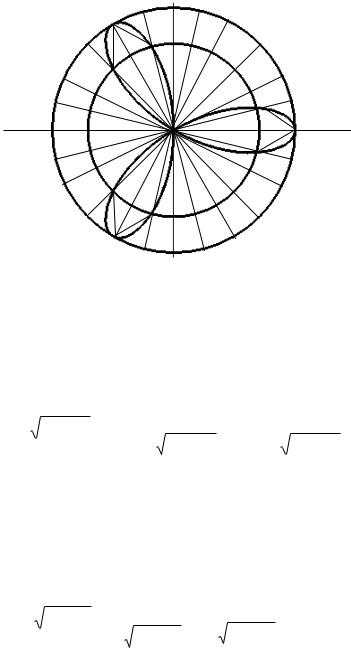
При построении линии cos3 , которая называется трехлепестковой розой (рис. 1.12), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
мы заготовили полярную сетку. |
Затем |
провели лучи, которые составляют с полярной осью уг- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
лы, |
указанные в табл. 1.1 |
|
через |
|
|
|
|
радиан, или 150. |
|
|
Провели две окружности с радиусами |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
равными 1 и  22 . Соединяя полученные точки отрезками линий (на рис. 1.12 они указаны пунк-
22 . Соединяя полученные точки отрезками линий (на рис. 1.12 они указаны пунк-
тиром), мы получили ломаную линию, схематически показывающую строение нашей кривой. Увеличивая число точек, определяемых на линии, можно, таким образом, получить ломаную, как угодно близко прилегающую к линии cos3 .
15
|
|
|
|
7 /12 |
|
/ 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
5 /12 |
|
|
|
|
||||||||
|
|
2 / 3 |
|
|
|
|
|
|
/ 3 |
|
|
|
|
|||||
|
3 / 4 |
|
|
|
|
|
|
|
|
|
/ 4 |
|
|
|
||||
5 / 6 |
|
|
|
|
|
|
|
|
|
|
|
|
/ 6 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 /12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 /12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 /12 |
|
|
|
7 / 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
11 / 6 |
|
|
|
|
|
5 / 4 |
|
|
|
|
|
|
|
|
7 / 4 |
|
|
|
|||||
|
|
4 / 3 |
|
|
|
|
|
|
5 / 3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
19 /12 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
17 /123 / 2 |
|
|
|
|
|
|
|
|||||||
Рис. 1.12. Трехлепестковая роза cos3 |
|
|
|
|||||||||||||||
Для преобразования уравнения cos3 к декартовым координатам воспользуемся фор- |
||||||||||||||||||
мулами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y 2 |
; cos |
|
|
x |
; sin |
|
y |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
x2 y 2 |
|
x2 y 2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Выражая cos3 через cos и sin , имеем: |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
cos3 4cos3 3cos . |
|
|
|
|
||||||||||
Подставляя найденное значение cos3 |
в уравнение кривой и заменяя в нем |
, |
cos и |
|||||||||||||||
sin их выражениями через x и y , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
y |
2 |
4 |
|
x3 |
|
|
3 |
|
x |
|
|
|
|
|||
x |
|
|
|
|
|
|
|
, |
или |
|
|
|
||||||
|
|
|
x2 y2 3 |
|
x2 y2 |
|
|
|
||||||||||
|
|
x2 y2 2 4x3 3x x2 y2 . |
|
|
|
|
||||||||||||
Окончательно получим уравнение трехлепестковой розы в декартовых координатах |
|
|||||||||||||||||
|
|
|
|
x2 y2 2 |
x x2 3y2 . |
|
|
|
(1.8) |
|||||||||
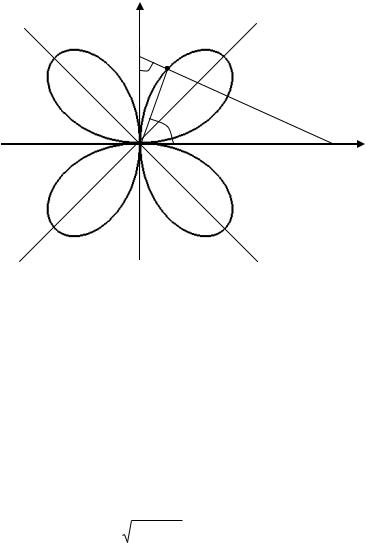
Пример 1.12. Отрезок AB постоянной длины 2a скользит своими концами по сторонам прямого угла. Из вершины прямого угла O на этот отрезок опущен перпендикуляр OM. Найти геометрическое место оснований этих перпендикуляров.
Решение. Пусть отрезок AB = 2a скользит по сторонам прямого угла своими концами. Точка M ( , ) – основание перпендикуляра, опущенного из вершины прямого угла O на отре-
зок AB (рис. 1.13).
Составим уравнение этого геометрического места точек в полярных координатах. Для это-
16
го поместим полюс в вершине прямого угла, а полярную ось O |
направим по катету OB . Рас- |
|||||||||||||||
смотрим треугольник OMB, у него OMB – прямой, так как точка М – основание перпендику- |
||||||||||||||||
ляра, опущенного на AB . Тогда OB cos . Из |
прямоугольного треугольника OAB опреде- |
|||||||||||||||
лим OB . При этом используем то, что OAB будет равен MOB ( OMB подобен |
OAB ; |
|||||||||||||||
OBA в этих треугольниках общий). Итак, OAB . |
|
|
|
|
|
|
||||||||||
|
|
OB AB sin 2a sin и OB cos AB sin cos 2a sin cos a sin 2 . |
|
|||||||||||||
Кривая |
a sin 2 |
называется четырехлепестковой розой. Если ограничиться углами |
||||||||||||||
0 |
, |
|
то |
( ) a sin 2 |
принимает |
наибольшее |
значении |
при |
|
|
, |
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
|
|
|
a . |
Наименьшее значение 0 при 0 и |
|
|
, |
так |
как |
||||
asin |
|
a sin |
|
|
||||||||||||
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
a sin 0 0 |
и |
|
|
2 |
|
|
0 . Остальные значения |
можно получить, если под- |
||||||||
a sin |
|
a sin |
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
ставить в уравнение a sin 2 соответствующие значения .
Y
A
M
B
X ,
Рис. 1.13. Четырехлепестковая роза a sin 2
Пример 1.13. Построить кривую
a sin 2 |
(1.9) |
и найти ее уравнение в декартовых координатах.
Решение. Кривая a sin 2 является четырехлепестковой розой. Ее уравнение в декартовых координатах можно получить, если использовать формулы
x2 y 2 ;
17

cos |
x |
; |
|||
|
|
||||
x2 y 2 |
|||||
|
|
|
|||
sin |
|
y |
. |
||
|
|
|
|||
|
x2 y 2 |
||||
|
|
|
|||
Подстановка этих формул в уравнение кривой дает
x2 y2 2a |
|
y |
|
x |
, |
|
x2 |
y2 |
x2 y2 |
||||
|
|
|
или, после упрощения,
x2 y2 3 2axy .
Окончательно получаем уравнение четырехлепестковой розы в декартовых координатах
x2 y2 3 4a2 x2 y2 . |
(1.10) |
|||
Сравнивая уравнения четырехлепестковой розы в полярной и декартовой системах коор- |
||||
динат, видим преимущество полярного уравнения a sin 2 |
– оно проще и удобнее при по- |
|||
строении кривой. |
|
|
|
|
Построим таблицу значений и , придавая значения |
, равные, |
k |
, k 0, 1, 2, 3,... |
|
12 |
||||
|
|
|
||
(табл.1.2). Затем построим полярную сетку, для чего проведем лучи, составляющие с полярной осью указанные в табл.1.2 углы. Далее, соединив полученные точки плавной линией, получим в I и IV четвертях, а затем и всю кривую, используя симметрию, относительно начала координат.
Замечание. Из уравнения x2 y2 3 4a2 x2 y2 видно, что если точка с координатами (x, y) удовлетворяет уравнению, то и точки с координатами ( x, y) , (x, y) и ( x, y) также удовле-
творяют этому уравнению. Следовательно, график функции симметричен относительно начала координат и координатных осей ОX и ОY. Поэтому таблицу значений функции можно было со-
ставить для 0 2 , а затем отобразить график функции симметрично относительно коорди-
натных осей. Из табл. 1.2 видно, что полученные значения , при заданном угле , повторя-
ются в каждой четверти, поэтому полярную сетку строим следующим образом: проводим лучи, которые составляют с полярной осью углы, указанные в табл. 1.2. Затем строим окружности ра-
диусов R 0,5a , |
R |
3 |
a , R a . Далее отмети точки пересечения этих окружностей с луча- |
|||||||||
|
||||||||||||
1 |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ми в каждом из четырех промежутков 0 |
|
, |
|
, |
3 |
, |
3 |
2 . Соединив |
||||
2 |
2 |
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||||
эти точки плавной линией, получим искомую кривую (рис.1.14).
18
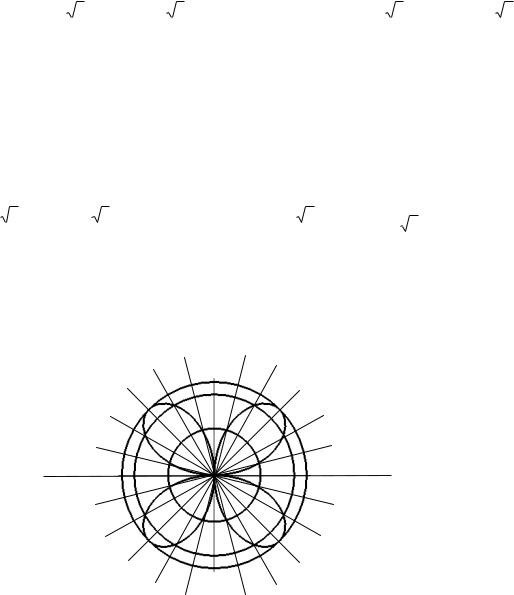
Таблица 1.2
Значения функции a sin 2
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
7 |
|
|
2 |
|
|
|
3 |
|
|
|
5 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
4 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
12 |
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
6 |
|
|||||||||||||||||
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
5 |
|
|
|
|
|
|
7 |
|
|
4 |
|
|
|
3 |
|
|
|
5 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|||||||||||||||||
|
a sin 2 |
|
|
0 |
|
|
|
|
0,5а |
|
3 |
|
|
|
а |
|
3 |
|
|
|
0,5а |
|
|
0 |
|
|
|
|
|
-0,5а |
|
3 |
|
|
|
-а |
|
|
3 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 а |
|
2 |
|
а |
2 |
а |
|
2 а |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
13 |
|
7 |
|
5 |
|
4 |
|
17 |
|
|
3 |
|
19 |
|
|
5 |
|
|
|
7 |
|
|
11 |
|
23 |
|
|
2 |
||||||||||||||||||||||||||||||||||
11 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
|
6 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
11 |
|
2 |
|
13 |
|
7 |
|
5 |
|
8 |
|
17 |
|
|
3 |
|
19 |
10 |
|
|
|
7 |
|
|
11 |
|
23 |
|
|
4 |
||||||||||||||||||||||||||||||||||||||
|
6 |
|
|
|
|
|
6 |
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
6 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
6 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
- |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
0,5а |
|
|
2 а |
|
|
а |
|
|
|
2 а |
|
0,5а |
|
|
0 |
|
|
2 |
а |
- а |
|
|
|
|
3 |
а |
|
|
|
0 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
0,5а |
|
|
0,5а |
|
|
|
2 |
0,5а |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 /12 |
/ 2 |
5 /12 |
|
2 / 3 |
/ 3 |
3 / 4 |
/ 4 |
5 / 6 |
/ 6 |
|
|
11 /12 |
/12 |
|
0, 2 |
|
|
13 /12 |
23 /12 |
7 / 6 |
11 / 6 |
5 / 4 |
7 / 4 |
4 / 3 |
5 / 3 |
|
19 /12 |
|
|
17 /123 / 2 |
|
Рис. 1.14. Построение четырехлепестковой розы с использованием полярной сетки
1.3.2. Лемниската Бернулли
Лемнискаты – это плоские алгебраические кривые порядка 2n , произведение расстояний каждой точки которых до заданных точек (фокусов) F1, F2 , ..., Fn равно заданному числу r (ра-
19
диусу лемнискаты). Уравнение лемнискаты в декартовых прямоугольных координатах имеет вид
|
|
z z1 z z1 ... z z1 |
|
rn , |
r 0, |
z x iy. |
|
||||
|
|
|
|
||||||||
Окружность есть лемниската с одним фокусом, овал Кассини – лемниската с двумя фоку- |
|||||||||||
сами. |
|
|
|
|
|
|
|
|
|
|
|
Пример 1.14. Составить уравнение геометрического места точек, произведение расстоя- |
|||||||||||
ний которых до двух данных точек |
F (a,0) и F ( a,0) есть величина постоянная, равная a2 . |
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
Решение. Пусть точка M(x,y) лежит на искомом геометрическом месте. Согласно условию |
|||||||||||
задачи |
MF MF a2 , |
где |
MF |
(x a)2 y2 , |
MF |
(x a)2 y2 . |
Тогда |
||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
(x a)2 |
y2 (x a)2 y2 |
a2 . |
Упростим это уравнение, для чего обе части его возведем в |
||||||||
квадрат:
(x a)2 y2 (x a)2 y2 a4 ,
x2 2ax a2 y2 x2 2ax a2 y2 a4 ,
x2 a2 y2 2ax x2 a2 y2 2ax a4 ,
x2 a2 y2 2 4a2 x2 a4 .
или
x2 y2 2 2 x2 y2 a2 a4 4a2 x2 a4 ,
x2 y2 2 2a2 x2 2a2 y2 ,
x2 y2 2 2a2 x2 y2 .
Найдено уравнение алгебраической кривой 4-го порядка, которая называется лемнискатой Бернулли (рис. 1.15).
Перейдем к полярным координатам, используя формулы (1.1):
2 2a2 2 cos2 2 sin2 ,
(1.12)
2 2a2 cos 2 .
20
