Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3007

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.84 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

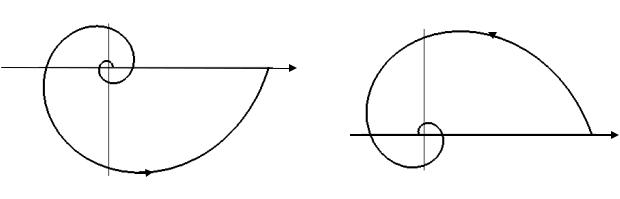
	k
знаменателем e		2 .
									Таблица 1.6
		Полярные координаты точек логарифмической спирали 2ek


				2	0		2
				2	0		2
			2e k	2e k / 2	2		2ek / 2	2e k

Когда угол неограниченно возрастает, то						также неограниченно растет, а когда

, то полярный радиус стремится к нулю и кривая неограниченно приближается к полю-

су О, закручиваясь около него. Поэтому точка О называется асимптотической точкой логарифмической спирали. Кривая пересекает все лучи, выходящие из точки О под одним и тем же углом , при этом k ctg (рис. 1.26, а). На этом свойстве основано применение логарифмиче-

ских спиралей в технике. Например, нужный угол резания вращающихся ножей в режущих машинах обеспечивается выбором параметра соответствующей спирали.

Пример 1.21. Построить график функции a , a 0 .

Решение. При 0 будет 1. Если a 1 , то при значение и спираль развертывается против хода часовой стрелки (рис. 1.26, б). Если 0 a 1, то при полярный радиус 0 и спираль закручивается вокруг полюса против хода часовой стрелки, стремясь к своей асимптотической точке О (рис. 1.26 б).

Пример 1.21. Построить график функции a , a 0 .

а)

б)

Рис. 1.26. Логарифмическая спираль 2ek

Задачи и упражнения для самостоятельной работы

1.11.Какой диапазон параметра соответствует тому, что спираль Архимеда сделает четыре первых полных оборота? Построить кривую.

1.12.Построить кривую e .

1.5. Некоторые важные кривые

1.5.1. Конхоиды

Конхоидой называется кривая, получающая при увеличении или уменьшении радиусвектора каждой точки данной кривой на постоянный отрезок b. Если уравнение кривой в полярных координатах имеет вид f ( ) , то уравнение конхоиды будет f ( ) b . Конхоида

прямой x a ‒ конхоида Никомеда, конхоида окружности – улитка Паскаля.

Конхоида Никомеда – плоская алгебраическая кривая четвертого порядка, уравнение кото-

рой в декартовых координатах имеет вид
x2 y2 x a 2 b2 x2 ,			a 0 ,	b 0 .	(1.23)
Полярное уравнение конхоиды принимает вид
	a	b ,			(1.24)

	cos
знак “+” соответствует правой ветви кривой, а знак “-“			– левой ветви (рис. 1.27). Асимптота
кривой x a для обеих ветвей.

Конхоида Никомеда названа по имени древнегреческого математика III-II века до н.э. Ни-

комеда, который применял ее для решения задачи о трисекции угла.
Y			Y				Y

	b				b			b
					b


0	a	X	0	a		X	0 a		X

а)		б)				в)
	Рис. 1.27. Конхоида	a	b :	а) b a ;	б) b a ;	в) b a

		cos

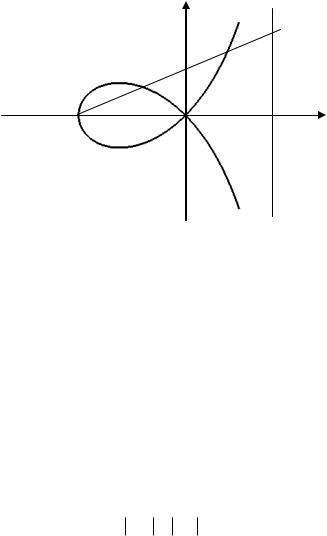
1.5.2. Строфоида

Строфоида – плоская алгебраическая кривая третьего порядка (рис. 1.28), уравнение которой в декартовых координатах имеет вид

y2 x2

a x

, a 0 .

(1.25)

a x

а в полярных координатах

cos 2

(1.26)

cos

Характеристическое свойство строфоиды состоит в следующем: для всякого луча, исхо-

дящего из точки A( a,0) , выполняется равенство

(рис. 1.28). Начало коорди-

нат – узловая точка с касательными y x . Асимптота x a . Площадь петли S 2a2

1/ 2 a2

(см. рис. 1.28). Площадь между кривой и асимптотой S2 2a2

1/ 2 a2 . Строфоида относится к

так называемым узлам.

-a

Рис. 1.28. Строфоида a	cos 2
	cos

1.5.3. Улитка Паскаля
Уравнение улитки Паскаля в декартовых координатах имеет вид
x2 y2 2ax b2 x2 y2 , a 0 , b 0 .		(1.27)
Уравнение кривой в полярных координатах при a b
2a cos b .		(1.28)

Характеристическое свойство улитки Паскаля состоит в следующем: для всякого луча, исходящего из точки О, выполняется равенство BM BN b const (рис. 1.29).

Улитка Паскаля названа по имени выдающегося французского математика Э. Паскаля (1-я половина XVII в.), впервые рассмотревшего ее.

Рис. 1.29. Улитка Паскаля 2a cos b
1.5.4. Кривая Каппа
Уравнение кривой Каппа (рис. 1.30) в полярной системе координат имеет вид
a ctg .	(1.29)
Переходя в уравнение кривой к прямоугольным декартовым координатам, получим
x2 y2 y2 a2 x2 ,	(1.30)

откуда следует, что каппа представляет собой алгебраическую кривую четвертого порядка, симметричную относительно осей координат.

Так как
	F(x, y) x2 y2 y2 a2 x2 и F 2xy 2a2 x ,		F 2x2 y 4 y3 ,
	x		y
то при x 0 , y 0 имеем Fx 0 , Fy 0 . Следовательно,		начало координат есть особая точка.
Поскольку вторая производная по аргументу x , равная F		2y2	2a2 при x 0 , y 0 отлич-
	xx
на от нуля,	то начало координат является двойной особой точкой. Заметим, что F			F F 0
			xy	xx yy
при x 0 ,	y 0 . Отсюда следует, что начало координат есть точка самоприкосновения (узло-
вая точка). Асимптотами кривой являются прямые y a .

Y a

-a

Рис. 1.30. Кривая Каппа a ctg

1.5.5. Кохлеоида

Уравнение кохлеоиды (рис. 1.31) в полярных координатах имеет вид

			a	sin	.	(1.31)


Если 0 , то a ; если же k			( k 0, 1, 2,... ),			то 0 .
Так как	sin	– четная функция, то кривая симметрична относительно полярной оси.


При		0 , причем радиус-вектор последовательно описывает затухающие

лепестки, вершины которых достигаются при значениях , являющихся корнями уравнения tg (рис. 1.31). Кохлеоида обладает следующим свойством: каждая прямая, проведенная

через полюс О, пересекает кривую в точках, касательные в которых проходят через одну и ту же точку.

Рис. 1.31. Кохлеоида a sin

1.5.6. Овал Кассини

Овал Кассини определяется как геометрическое место точек, для которых произведение расстояний до двух заданных фиксированных точек F1(c;0) и F2(-c;0) есть величина постоянная,

равная a2, то есть MF MF a2 (рис. 1.32).
1	2
Уравнение кривой в декартовых координатах
x2	y2 2 2c2 x2 y2 a4 c4 0 ,		c 0 ,	a 0 .	(1.32)
Уравнение в полярных координатах
	2 c2 cos2	c4 cos2 (a4		c4 ) .	(1.33)

При a 0 овал вырождается в две точки F1 и F2. При возрастании a от 0 до с около точек F1 и F2 появляются замкнутые линии, которые, увеличиваясь в размерах, смыкаются при a c , образовав лемнискату. При дальнейшем увеличении a овал представляет собой замкнутую ли-

нию, имеющую “талию”. При a c 2 “талия” исчезает. При последующем увеличении пара-

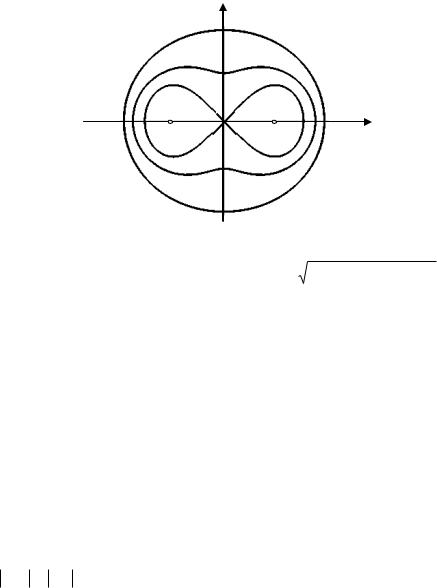
метра a кривые примут форму эллипсоидных овалов. Овал Кассини относится к лемнискатам. Рассматривался Дж. Кассини (XVII в.) при попытках определить орбиту Земли.

F2	0	F1	X,

Рис. 1.32. Овалы Кассини 2 c2 cos2 c4 cos2 (a4 c4 )

1.5.7. Циссоида

Циссоида – плоская алгебраическая кривая третьего порядка (рис. 1.33), уравнение которой в декартовых координатах имеет вид

x3 y2 (x a) 0 ,			a 0 .	(1.34)
Уравнение в полярных координатах
a	sin 2	.		(1.33)
a	cos	.		(1.33)
	cos

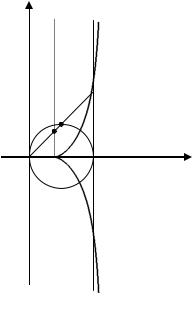
Характеристическое свойство циссоиды: для всякого луча, исходящего из точки O, выполняется равенство OM BC (рис. 1.33). Асимптотой циссоиды является вертикальная прямая x a . Циссоида симметрична относительно оси абсцисс. Площадь между кривой и асимптотой

равна S 3 a2 / 4 . Греческий математик Диоклес (III в. до н.э.) рассматривал циссоиду в связи с решением задачи об удвоении куба.


Рис. 1.33. Циссоида a					sin 2
					cos

Задачи и упражнения для самостоятельной работы
1.13. Построить кривые: а) 4 2cos ;		б)	3 3cos ;				в) 1 2 cos .
5			6				4
1.14. Построить кривые: а)		; б)				;	в)		.

								2 3cos
	6 3cos			1 cos

ГЛАВА 2. ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ФУНКЦИЙ

2.1. Основные понятия

Параметрические уравнения играют важную роль, например, в механике, где координаты x и у движущейся точки M x, y рассматриваются как функции времени (уравнения движения).

При описании уравнений геометрических мест (линий) иногда оказывается более удобным выразить координаты х и у произвольной точки этого геометрического места через некоторую вспомогательную величину t, которую называют параметром, т.е. представить х и у в виде:

x t ,	(2.1)
	(2.1)
y t .

Такое представление искомой линии называется параметрическим, а уравнения системы

(2.1) называют параметрическими уравнениями данной линии.

В качестве параметра может быть взято не обязательно время, а, например, некоторый угол между вектором, идущим из фиксированной точки интересующей нас кривой, и заданной осью, или каким то образом выбранная алгебраическая зависимость переменных x и у от некоторого параметра t.

Исключение параметра t из системы (2.1) (если оно возможно) приводит к уравнению, связывающему х и у, то есть к обычному уравнению линии вида f x, y 0 .

Для приближенного построения графика кривой, заданной параметрически, достаточно построить таблицу значений x и у в зависимости от возможных значений параметра t (табл. 2.1). При этом надо учитывать t1 t2 ... tn .

Таблица 2.1

Значения x и у от параметра t

t1	t	…	tn
	2
x1	x2	…	xn
y1	y2	…	yn

Затем построить на плоскости декартову систему координат, отметить на ней точки с координатами (x1, y1), (x2 , y2 ),...,(xn , yn ) и соединить эти точки в порядке увеличения параметра t.

Параметрически задавать кривую можно в любой системе координат, но мы будем рассматривать параметрическое задание кривой только в декартовой системе.

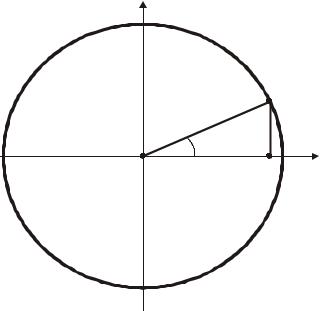
Пример 2.1. Составить параметрические уравнения окружности.

Решение. Рассмотрим окружность радиуса R с центром в начале координат. Пусть M x, y – произвольная точка окружности (рис 2.1).

Спроектируем точку М на ось ОХ и рассмотрим прямоугольный треугольник ОАМ. Угол АОМ обозначим через t. Тогда декартовы координаты х и у точки М будут связаны с параметром t равенствами

x R cost,

(2.2)

y Rsin t.

Это и есть параметрические уравнения окружности.

Yy
			M
	R	y
		y
	t
0	x	A	x
			X
Рис. 2.1. Окружность, с центром в начале координат

Если исключить параметр t из этих уравнений, получим уравнение окружности в декарто-

вых координатах. Возведем обе части равенств в системе (2.2) в квадрат получим:

R2 cos2 t,

R2 sin2 t.

R2 cos2 t sin 2 t

Теперь сложим первое уравнение со вторым, получим

x2 y2

или

уравнение x2 y2

– это уравнение окружности с центром в начале координат и радиусом,

равным R в декартовой системе координат.

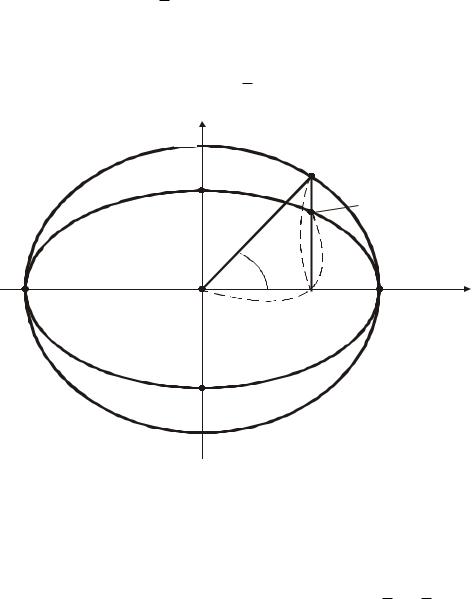
Пример 2.2. Cоставить параметрические уравнения эллипса.

Решение. Пусть

OB b,

OA a,

k –

коэффициент деформации окружности в на-

правлении NM (рис. 2.2). Пусть M x, y

N x, y – соответствующая точка

– точка эллипса, и

окружности, где

x X ,

y b Y .

(2.3)

N(X,Y)

B(0,b)

M(x,y)

A(a,0)

A'(-a,0)

x = X

B'(0,-b)

Рис. 2.2. Эллипс с центром симметрии в начале координат

За параметр t примем угол, образованный радиусом ON с положительным направлением

оси

ОХ:

t NOA.

Рассмотрим

прямоугольный

треугольник

ONP:

OP x a cost;

PN y a sin t .

Используя формулы (2.3),

получим

x X a cost, y b Y

b asin t bsin t .

Таким образом, параметрические уравнения эллипса с полуосями a и b имеет вид:

x a cost,

0, 2

(2.4)

bsin t.

Исключив из этих уравнений параметр t, получим: cost	x	,	sin t	y	. Возведем в квад-
	a			b

рат каждое из последних равенств и сложим, получим выражение вида

x2 y2 a2 b2

	2		2	x 2		y 2
cos		t sin		t			или

				a	b

1 – это каноническое уравнение эллипса.

Имея параметрические уравнения кривой можно построить ее по точкам.

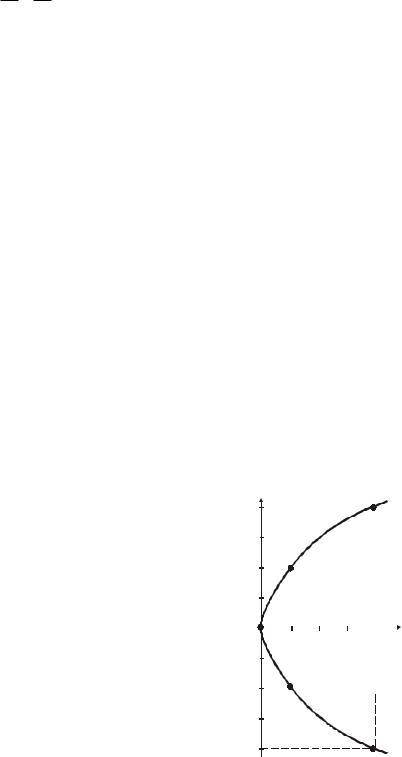
Пример 2.3. Построить кривую

x t 2 ,

y 2t.

Решение. Составим таблицу значений функции в зависимости от возможных значений параметра t (табл. 2.2).

							Таблица 2.2
			Значения функции		x t 2	,
			Значения функции
					y 2t.
t	-2	-1		0	1	2	…
x	4	1		0	1	4	…
y	-4	2		0	2	4	…

Нанося точки с соответствующими координатами (х, у) на плоскость OXY и соединяя их линией, получим искомую кривую. Эта кривая – парабола. Действительно, исключая параметр t

из уравнения y 2t , затем подставим	t	y	в уравнение x t	2			y		2
					,	имеем	x		или
					,	имеем	x		или
		2						2

y2 4x ‒ это парабола с вершиной в точке		О(0, 0)			и	симметричной относительно оси ОХ
(рис. 2.3).
	Y 4
	Y 4
3




2



1










0			1 2	3			4	X


-1



-2

-3

-4

Рис. 2.3. Парабола с вершиной в начале координат

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.78 Mб02995.pdf
#
15.11.20222.79 Mб02996.pdf
#
15.11.20222.82 Mб03002.pdf
#
15.11.20222.82 Mб13004.pdf
#
15.11.20222.84 Mб03006.pdf
#
15.11.20222.84 Mб13007.pdf
#
15.11.20222.85 Mб33008.pdf
#
15.11.20222.85 Mб43009.pdf
#
15.11.20222.85 Mб03010.pdf
#
15.11.20222.85 Mб13011.pdf
#
15.11.20222.85 Mб43012.pdf