
3007
.pdf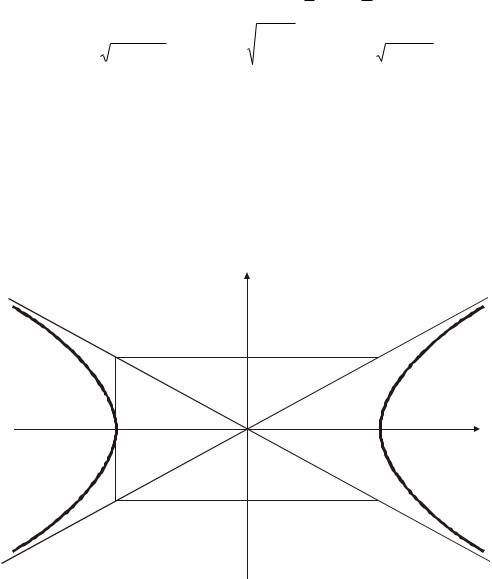
Пример 2.4. Кривая задана параметрическими уравнениями
x a sec t, |
t , |
|
|
y b tgt. |
|
Найти уравнение линии в декартовых координатах.
Решение. По условию
|
a |
|
x a sect |
|
, |
|
||
|
cost |
|
|
|
|
y b tgt. |
|
|
Выразим из последнего равенства параметр: cost ax , tgt by или
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
a2 |
|
|
|
|
|
|
|
|
|||
tgt |
|
1 cos2 t |
; |
|
y |
|
|
|
x2 |
|
; |
|
|
y |
|
x2 a2 |
. |
|||||||||||
|
|
cost |
|
|
|
|
b |
|
|
|
a |
|
|
|
b |
a |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||
Возводя обе части последнего равенства в квадрат, получим |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
y |
2 |
|
x2 a2 |
|
|
или |
|
|
y2 |
|
|
x2 |
1 . |
|
|
||||||||
|
|
|
|
|
b2 |
|
a2 |
|
|
|
|
b2 |
|
a2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Окончательно имеем |
x2 |
|
y2 |
1 |
|
– это каноническое уравнение гиперболы с центром в |
||||||||||||||||||||||
a2 |
b2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
начале координат (рис. 2.4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-a |
a |
0 |
|
x |
|
|
|
X |
|
|
-b |
|
|
|
|
|
|
|
|
|
|
Рис. 2.4. Гипербола симметричная относительно начала координат
41

Итак, кривая
координат.
x a sec t, |
|
x2 |
|
y2 |
|||
|
– это гипербола |
|
|
|
|
|
1 с центром симметрии в начале |
|
2 |
|
2 |
||||
y b tgt, |
|
a |
|
|
b |
|
|
Пример 2.5. Какая линия определяется параметрическими уравнениями
x t 2 ,
y t 2 ?
|
Решение. Исключим параметр t: t2 x , t2 |
y , следовательно y x , это уравнение пря- |
|
мой, |
проходящей через начало координат. |
Но в силу параметрических уравнений |
|
x t2 |
0, |
y t2 0 . Следовательно, данные параметрические уравнения определяют луч, на- |
|
правленный по биссектрисе I координатного угла (рис. 2.5).
yY |
|
0 |
x |
X |
Рис. 2.5. Графическое изображение к примеру 2.5
Пример 2.6. Какая линия определяется уравнениями
x sin t,
y cosect ?
|
Решение. Так как y |
1 |
, то, исключив t, |
получим уравнение y |
1 |
, выражающее об- |
|||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
sin t |
|
|
|
|
x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 и |
|||||
ратно |
|
пропорциональную |
зависимость |
величин |
x и у. |
В силу ограничений |
sin t |
||||||||||
|
cos ect |
|
|
|
1 |
|
1 заключаем, |
что |
линия, заданная |
параметрическими уравнениями |
|||||||
|
|
|
|
||||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||
|
|
sin t |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x sin t, |
y cos ect , имеет вид, изображенный на рис. 2.6. |
|
|
|
|
|
||||||||||
42

yY
-1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
x |
||||||||
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
X |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.6. Графическое изображение кривой к примеру 2.6 |
|
|
|||||||||||
|
|
|
|
Задачи и упражнения для самостоятельной работы |
|
|
|
|||||||||
2.1. Какая линия определяется параметрическими уравнениями |
|
|
|
|
|
|||||||||||
x cos t, |
|
|
x 2t, |
|
x cos2 t, |
x sin t, |
|
|
x 5t, |
|
x sin2 t, |
|||||
а) |
|
|
|
|
|
|
|
г) |
|
|
|
|
|
|
||
y cos2 |
t; |
б) |
y 4t; |
в) |
|
y sin2 t; |
y sin2 t; |
д) |
|
y 7t; |
е) |
|
y cos2 t. |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2.2. Написать параметрические уравнения окружности с центром в начале координат и радиусом 5.
2.3. Написать параметрическое уравнение эллипса с полуосями a = 7, b = 3 (центр эллипса находится в точке (0,0)).
2.4. Написать параметрическое уравнение гиперболы с полуосями a = 3, b = 7 (центр симметрии находится в точке (0,0)).
2.5. Написать параметрическое уравнение параболы с вершиной в точке (0,0) и ориентированной вдоль положительных значений оси OY.
2.2. Некоторые кривые, заданные параметрически
2.2.1. Циклоида
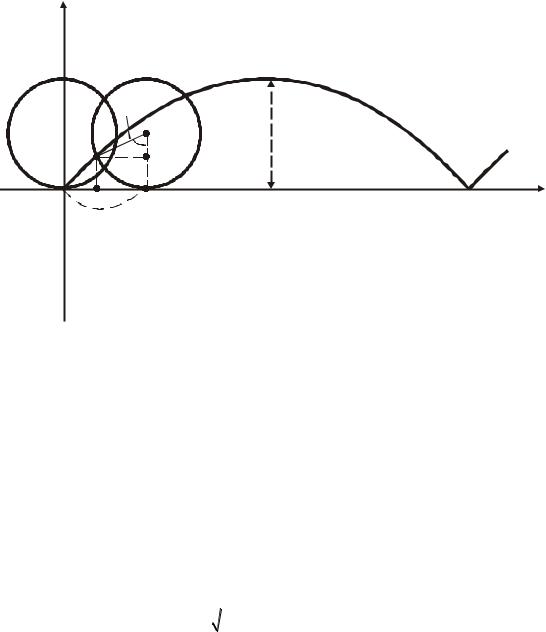
Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 2.7).
Выведем параметрические уравнения циклоиды, приняв прямую линию за ось ОХ, предполагая, что радиус, катящейся окружности равен а и в начальный момент движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса KC, где К – точка касания окружности с осью ОХ. Так как качение окружности проис-
ходит без скольжения, то OK MK at .
43
Y |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
C |
2a |
|
|
|
M |
t |
|
|
|
|
|
Q |
|
|
|
||
|
|
|
|
|
|
|
O |
P |
K |
|
a |
a |
xX |
|
at |
|
|
|
|
|
|
|
|
|
Рис. 2.7. Циклоида |
|
|
Отсюда для координат движущейся точки М циклоиды получим следующие выражения: x OP OK PK OK MQ at asin t a t sin t ,
y PM KC QC a a cost a 1 cost .
Таким образом, параметрические уравнения циклоиды
x a t sin t , |
|
|
|
|
t , |
(2.5) |
|
y a 1 cos t . |
|||
|
|
||
|
|
|
|
|
|
|
В декартовых координатах уравнение циклоиды:
|
|
|
|
|
a cos |
x |
y 2a y |
a y; |
a 0 . |
|
a |
|||
|
|
|
|
2.2.2. Астроида
Астроида – это кривая, определяемая параметрическими уравнениями
x a cos3 t, |
|
|
(2.6) |
|
|
y a sin 3 t. |
|
|
|
Определим значения x и y для различных значений t и занесем их в табл. 2.3. Так как
тригонометрические функции синус и косинус являются периодическими с периодом 2 , то t 0, 2 .
44

Таблица 2.3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a cos3 t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Значения функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y a sin 3 t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
5 |
|
|
|
||||||
|
6 |
|
|
4 |
|
3 |
|
|
2 |
|
|
3 |
|
4 |
|
|
6 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
x |
1 |
|
0,6495 |
|
0,3535 |
0,125 |
|
0 |
|
|
-0,125 |
-0,3535 |
0,64 |
-1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
95 |
|
|
|
|
y |
0 |
|
0,125 |
|
0,3535 |
0,6495 |
1 |
|
|
0,6495 |
0,3535 |
0,12 |
|
0 |
|||||||||||||||||
|
|
|
|
5 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
t |
|
7 |
|
5 |
|
|
4 |
|
3 |
|
|
5 |
|
|
7 |
11 |
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6 |
|
4 |
|
|
3 |
|
2 |
|
|
3 |
|
|
4 |
|
6 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x |
-0,6495 |
-0,3535 |
|
-0,125 |
0 |
|
|
0,125 |
|
0,3535 |
0,6495 |
-1 |
|
||||||||||||||||||
y |
-0,125 |
-0,3535 |
|
-0,6495 |
-1 |
|
|
-0,6495 |
|
-0,3535 |
-0,125 |
0 |
|
||||||||||||||||||
Исключив параметр t, можно найти уравнение астроиды в прямоугольной системе коорди-
нат. Из первого уравнения определим cos3 t , а из второго уравнения sin 3 t ; cos3 t ax , sin 3 t ay ,
|
|
|
|
1 |
|
|
1 |
|
||
|
x |
|
|
|
|
|
|
|||
|
3 |
|
y |
3 |
|
|||||
или |
cost |
|
|
|
, |
sin t |
|
|
. |
|
|
|
|
||||||||
|
a |
|
|
a |
|
|||||
Так как sin 2 t cos2 t 1, то возводя в квадрат обе части последних равенств, потом складывая их, получим:
|
|
|
1 |
|
2 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
||||
x 3 |
|
|
|
y 3 |
|
cos |
2 |
t sin |
2 |
t 1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
a |
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x 3 y 3 |
a 3 . |
|
|
|
|
|
(2.7) |
|||||||||||
На рис. 2.8 изображено геометрическое место точек, удовлетворяющее уравнению (2.6) |
||||||||||||||||||||||||||
или уравнению (2.7), т.е. построена астроида. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
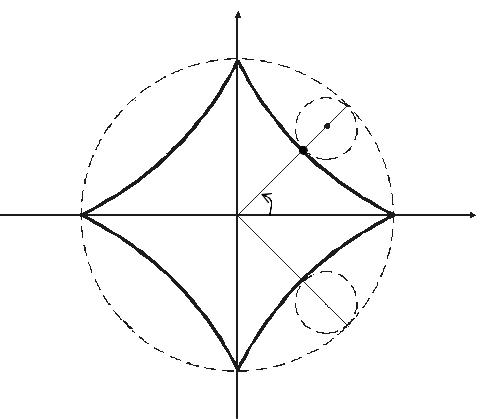
Окружность радиуса а – направляющая кривая L, окружность К радиуса |
a |
катится без |
||||||||||||||||||||||||
4 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
скольжения внутри нее. Тогда точка М окружности К описывает кривую с параметрическими уравнениями x acos3 t, y asin 3 t , т.е. астроиду.
45
Y a
|
|
K |
|
|
M |
L |
|
|
|
|
|
|
t |
|
|
0 |
|
a |
X |
|
|
|
Рис. 2.8. Астроида
2.2.3. Декартов лист
Декартов лист ‒ линия, которая состоит из петли и двух бесконечных ветвей (рис. 2.9). Декартов лист можно задать в декартовой системе координат уравнением
x3 y3 |
3axy 0; |
a 0 |
||
или полярных координатах через и : |
|
3a cos sin |
. |
|
|
||||
|
|
cos3 sin3 |
||
Параметрически декартов лист задается уравнениями вида:
|
3at |
|
|
|
|
|
|
x |
|
|
, |
|
|
|
|
1 t |
3 |
|
|
|
|||
|
|
|
где t tg MOx , |
t 1 и |
1 t . |
(2.8) |
|
|
3at 2 |
|
|||||
y |
|
, |
|
|
|
||
|
|
|
|
|
|
||
|
1 t |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь М – произвольная точка кривой. Начало координат О – узловая точка кривой. При1 t кривая проходит из второго квадранта через точку (0, 0) и точку А в точку (0, 0) ( t ), при t 1 кривая, начинаясь в точке (0, 0), располагается в четвертом квадран-
46
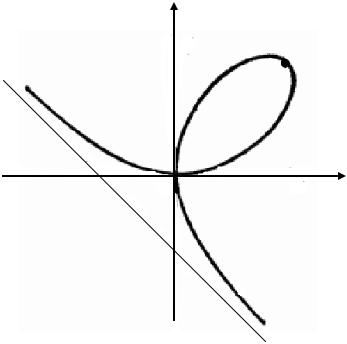
те. Оси координат – касательные к кривой в точке (0, 0). Асимптота описывается уравнением
|
|
3a |
|
3a |
|
|
x y a 0 . Вершина имеет координаты |
A |
; |
. |
|||
|
|
|||||
|
|
2 |
|
2 |
||
Y
А
- a |
0 |
X |
|
||
|
- a |
|
Рис. 2.9. Декартов лист при a 1
2.2.4. Циссоида
Циссоиду можно задать уравнением в декартовых координатах:
|
|
x3 y2 x a 0 или |
|||
в полярных координатах |
|
a sin2 |
|
atg sin . |
|
cos |
|||||
|
|
|
|||
Параметрические уравнения циссоиды имеют вид:
|
at 2 |
|
|
|
|
x |
|
, |
|
||
1 t 2 |
(2.9) |
||||
|
at 3 |
|
|
t . |
|
y |
|
|
, |
|
|
|
|
|
|
||
|
1 t |
2 |
|
|
|
|
|
|
|
|
|
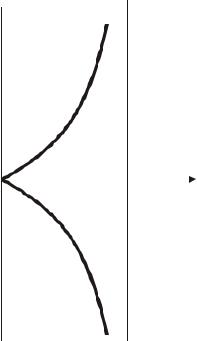
Уравнение x a описывает асимптоту кривой. Геометрическое место точек, удовлетворяющих уравнению (2.9) изображено на рис. 2.10.
47
Y  y
y
x = a
|
|
x |
|
|
|
0 |
a |
X |
|
|
Рис. 2.10. Циссоида
Задачи и упражнения для самостоятельной работы
2.6.Точки A(5, 0) и B(0, 5) принадлежат астроиде, симметричной относительно осей OХ и OY. Написать ее параметрические уравнения и построить кривую.
2.7.Одна арка циклоиды опирается на отрезок длиной 4π. Написать ее параметрические уравнения.
ГЛАВА 3. КРИВЫЕ ВТОРОГО ПОРЯДКА
Рассмотрим линии, определяемые уравнениями второй степени относительно переменных
x и y
Ax2 2Bxy Cy2 2Dx 2Ey F 0 , |
(3.1) |
причем по крайней мере один из коэффициентов A, B или C отличен от нуля. Такие линии называются линиями (кривыми) второго порядка. Можно утверждать, что уравнение (3.1) определяет на плоскости окружность, эллипс, гиперболу или параболу [10]. Перейдем к рассмотрению свойств этих кривых.
3.1. Окружность
Простейшей кривой второго порядка является окружность. По определению окружностью радиуса R с центром в точке M0 (x0 , y0 ) называется множество всех точек плоскости М таких,
что M0M R .
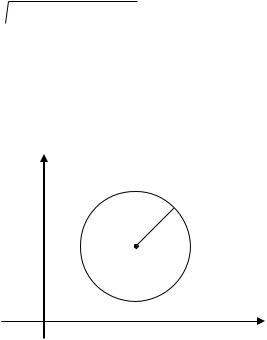
Пусть M (x, y) – произвольная точка окружности (рис. 3.1), тогда из условия M0M R получаем уравнение
48
 (x x0 )2 ( y y0 )2 R ,
(x x0 )2 ( y y0 )2 R ,
возведя в квадрат обе части уравнения получим
(x x )2 |
( y y )2 |
R2 . |
(3.2) |
0 |
0 |
|
|
Уравнение (3.2) – это уравнение окружности радиуса R с центром в точке M0 (x0 , y0 ) .
Y
 M
M
R
M
0 |
X |
Рис. 3.1. Окружность радиуса R с центром в точке M0 (x0 , y0 )
Полагая x0 0 и y0 0 , получим уравнение окружности с центром в начале координат x2 y2 R2 .
Задачи и упражнения для самостоятельной работы
3.1. Написать уравнение окружности с центром в точке С( 4,3) и радиусам равным 5, построить ее. Лежат ли на этой окружности точки А(-1,-1); В(3,2); О(0,0)?
3.2. Написать уравнение окружности с центром в точке С(2, 3) , проходящей через точку А(5,1), построить ее.
3.2.Эллипс
3.2.1.Каноническое уравнение эллипса
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем
расстояние между фокусами. |
|
|
Обозначим фокусы через F1 и F2 , расстояние между ними как |
2с , а сумму расстояний от |
|
произвольной точки эллипса до фокусов – через 2а . Отметим, что по определению |
2а 2c . |
|
Для вывода уравнения эллипса выберем систему координат OXY так, чтобы фокусы F1 |
и F2 ле- |
|
жали на оси OX, а начало координат совпадало с серединой отрезка |
F1F2 . Тогда фокусы будут |
|
иметь следующие координаты F1(-c,0) и F2(c,0) (рис. 3.2). |
|
|
49

Y M(x,y)
|
F1(-c,0) |
0 |
F2(c,0) X |
|
||
|
Рис. 3.2. Геометрическое построение к выводу уравнения эллипса |
|
||||
|
Пусть M (x, y) – произвольная точка |
эллипса. Тогда, согласно определению |
эллипса, |
|||
MF MF 2а , то есть |
|
|
|
|
||
1 |
2 |
|
|
|
|
|
|
(x с)2 y2 (x с)2 y2 2а . |
|
||||
|
Преобразуем полученное уравнение |
|
|
|
|
|
|
(x с)2 y2 2а (x с)2 y2 , |
|
||||
|
x2 2сx с2 y2 4а2 4a (x с)2 y2 x2 2сx с2 y2 |
|
||||
|
a (x с)2 y2 а2 cx , |
|
||||
|
а2 x2 2а2сx а2с2 а2 y2 а4 2а2сx с2 x2 , |
|
||||
|
(а2 с2 )x2 а2 y2 а2 (а2 с2 ) . |
|
||||
|
Так как а c , а2 с2 0 . Положим |
|
|
|
|
|
|
|
а2 с2 |
b2 . |
(3.3) |
||
|
Тогда последнее уравнение примет вид b2 x2 а2 y2 а2b2 , разделив которое на |
а2b2 , по- |
||||
лучим |
|
|
|
|
||
|
|
x2 |
|
y2 |
1 . |
(3.4) |
|
|
а2 |
b2 |
|||
|
|
|
|
|
||
Уравнение (3.4) – каноническое уравнение эллипса.
3.2.2. Исследование формы эллипса
Установим форму эллипса, пользуясь его каноническим уравнением (3.4).
1. Симметрия эллипса. Уравнение (3.4) содержит x и y только в четных степенях, поэтому если точка (x,y) принадлежит эллипсу, то ему также принадлежат точки (x,-y), (-x,y), (-x, -y). Следовательно, эллипс симметричен относительно координатных осей и начала координат.
Точку O(0,0) называют центром симметрии эллипса.
50
