
3007
.pdf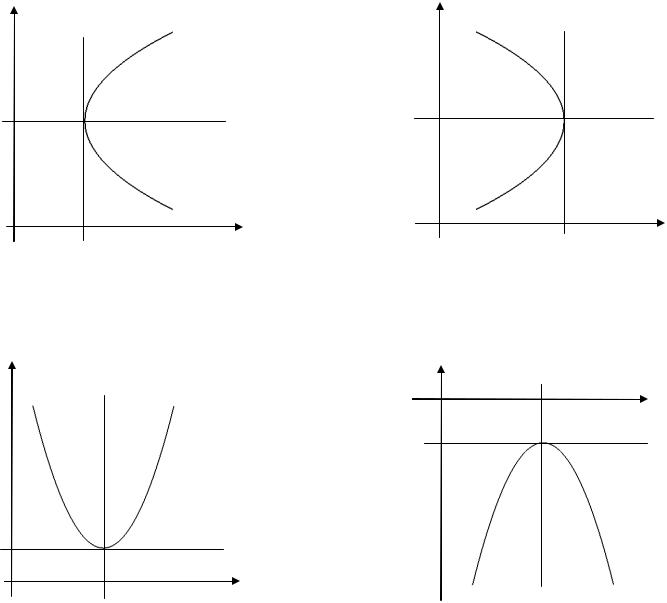
Уравнения вида
( y y )2 |
2 p(x x ) , |
( y y )2 2 p(x x ) , |
|
|
0 |
0 |
0 |
0 |
|
(x x )2 |
2 p( y y ) , |
(x x )2 |
2 p( y y ) , |
(3.13) |
0 |
0 |
0 |
0 |
|
где p 0 , определяют параболы с вершиной в точке O1(x0 , y0 ) , они изображены на рис. 3.12.
Y Y
y0
O
Y
y0
O
O1
x0 |
X |
( y y )2 |
2 p(x x ) |
0 |
0 |
O1 |
|
x0 |
X |
(x x )2 |
2 p( y y ) |
0 |
0 |
y0
O
Y
O
y0
O1
|
x0 |
X |
|
|
|
( y y )2 |
2 p(x x ) |
|
0 |
0 |
|
x0 X
O1
(x x0 )2 2 p( y y0 )
Рис. 3.12. Графики парабол, соответствующих уравнениям (3.13)
61
Уравнения (3.11), (3.12), (3.13) после преобразования (раскрыть скобки, привести подобные, ввести новые обозначения коэффициентов) можно записать с помощью единого уравнения вида
Ax2 Cy2 2Dx 2Ey F 0 , |
(3.14) |
где А и С не равны нулю одновременно.
Возникает вопрос: всякое ли уравнение (3.14) определяет одну из кривых (окружность, эллипс, гипербола, парабола) второго порядка? Ответ дает следующая теорема.
Теорема. Уравнение (3.14) всегда определяет: либо окружность при А = С; либо эллипс при А С 0 ; либо гиперболу при А С 0 ; либо параболу при А С 0 . При этом возможны случаи вырождения: для эллипса (окружности) – в точку или мнимый эллипс (окружность); для гиперболы – в пару пересекающихся прямых; для параболы – в пару параллельных прямых.
Пример 3.1. Определить вид кривой, привести уравнение к каноническому виду, изобра-
зить кривую: 2x2 5y2 12x 10 y 13 0. |
|
|
|
||||||
Решение. Так как А С 2 5 0 , |
то данное уравнение определяет эллипс. Выделяя пол- |
||||||||
ные квадраты и приведя подобные, уравнение можно привести к виду: |
|||||||||
2(x2 6x 9) 5( y2 2y 1) 18 5 13 0 |
|||||||||
|
2(x 3)2 5( y 1)2 |
36 , |
|||||||
|
|
2(x 3)2 |
5( y 1)2 |
||||||
|
|
|
|
|
|
|
|
|
1. |
|
|
|
36 |
36 |
|
||||
|
|
|
|
|
|
|
|||
Получим уравнение эллипса |
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 3)2 |
( y 1)2 |
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
18 |
|
7,2 |
||||
|
|
|
|
|
|
|
|||
с центром в точке (3,-1) и полуосями а |
|
18 , b |
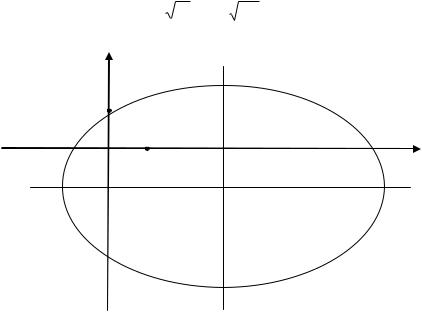
7,2 . Сделаем чертеж (рис. 3.13). |
||||||
Y |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
O |
1 |
|
|
|
|
|
3 |
|
X |
-1 |
|
|
|
O1 |
|
|
|
||
Рис. 3.13. Геометрическое построение к примеру 3.1
62
Пример 3.2. Определить вид кривой, привести уравнение к каноническому виду, изобразить кривую: x2 y2 6x 4y 4 0 .
Решение. Так как А С 1 ( 1) 0 , то данное уравнение определяет гиперболу. Выделяя полные квадраты и приведя подобные, уравнение можно привести к виду:
(x2 6x 9) ( y2 4y 4) 9 4 4 0
(x 3)2 ( y 2)2 9 .
Получим уравнение гиперболы
(x 3)2 |
( y 2)2 |
|||
|
|
|
1 |
|
9 |
9 |
|||
|
|
|||
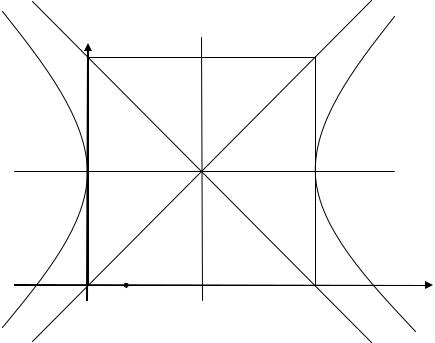
с центром в точке (3,2) и полуосями а 3 , b 3 . Сделаем чертеж (рис. 3.14).
Y
3 |
O1 |
1 
O
1 |
3 |
X |
Рис. 3.14. Геометрическое построение к примеру 3.2
Пример 3.3. Определить вид кривой, привести уравнение к каноническому виду, изобразить кривую: x2 10x 2y 21 0.
Решение. Так как А С 1 0 0 , то данное уравнение определяет параболу. Выделяя полные квадраты и приведя подобные, уравнение можно привести к виду:
x2 10x 25 2y 21 25 0 ,
(x 5)2 2y 4 .
Получим уравнение параболы
63
(x 5)2 2( y 2)
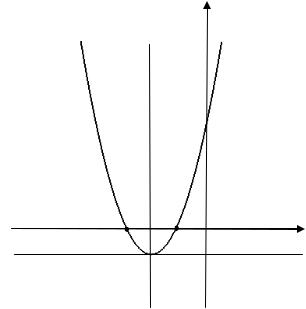
с вершиной в точке (-5,-2) и параметром p 1 . Найдем точки пересечения параболы с осями координат, для удобства построения. Точки пересечения с осью ОХ получаем при y=0, решая уравнение x2 10x 21 0 , находим точки x1 7 и x2 3 , значит, имеет точки (-7;0) и (-3;0). Точку пересечения с осью ОY получаем при x=0, решая уравнение 2 у 21 0 , находим точку у1 10,5 , значит точка (0;10,5). Сделаем чертеж (рис. 3.15).
Y
 10,5
10,5
-7 -5 -3 |
X |
|
O |
O1 |
-2 |
|
Рис. 3.15. Геометрическое построение к примеру 3.3
Задачи и упражнения для самостоятельной работы
3.13. Определить вид кривой, привести уравнение к каноническому виду, изобразить кри-
вую:
а) x2 y2 x 4 0 ; |
д) x2 3y2 5x 0 ; |
б) 4x2 9y2 8x 36 y 4 0 ; |
е) x2 2x y ; |
в) x2 2y2 3x y 5 0 ; |
ж) x2 4x y 0 ; |
г) 7x2 5y2 14x 20 y 22 0 ; |
з) y2 6x 2y 11 0 . |
3.6. Кривые второго порядка в полярных координатах или заданные параметрическим образом
Как показано в пункте 1.2 пример 1.7, все кривые второго порядка в полярной системе ко-
ординат имеют общее уравнение |
|
|
|
p |
|
|
. |
|
1 cos |
||
Еще раз отметим, что, если, если 1, то кривая, определяемая данным уравнением, есть
64
эллипс; если 1 , то кривая задает |
гиперболу; если 1 , то это есть парабола. |
p |
b2 |
– фо- |
|
a |
|||||
|
|
|
|
кальный параметр для эллипса и гиперболы. Для параболы p имеет тот же смысл, что и в уравнении в декартовой системе координат y2 2 px (то есть p – расстояние от фокуса до дирек-
трисы).
В пункте 2.1 пример 2.1– 2.4 приводятся параметрические уравнения окружности, эллипса, параболы и гиперболы.
Задачи и упражнения для самостоятельной работы
3.14. Перейти к декартовым координатам, привести уравнение к каноническому виду и по-
строить кривую: а) |
|
4 |
; |
б) |
|
|
6 |
; в) |
|
1 |
; |
|
|
|
|
||||||||||
2 3cos |
1 cos |
2 cos |
||||||||||
г) |
5 |
|
; |
д) |
3 |
|
. |
|
|
|
||
|
|
|
|
|
||||||||
6 3sin |
3 sin |
|
|
|
||||||||
3.15. Написать параметрическое уравнение следующих кривых и построить их графики:
а) x2 y2 9 ; б) |
x2 |
|
y2 |
1; |
в) |
x2 |
|
y2 |
1 ; |
г) y2 6x ; |
д) x2 4y . |
|
|
|
|
||||||||
|
9 |
4 |
|
|
25 |
16 |
|
|
|
||
ГЛАВА 4. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
4.1. Вычисление площадей плоских фигур
Пусть в полярной системе координат имеем кривую, заданную уравнением
( ) ,
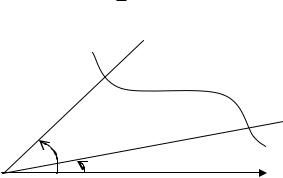
где ( ) – непрерывная функция при . Тогда площадь криволинейного сектора, ограниченного кривой ( ) и двумя полярными радиусами, составляющими с полярной осью углы и (рис. 4.1), вычисляется по формуле:
S 1 2 ( )d . 2
( )
|
|
|
|
0 |
|
Рис. 4.1. Криволинейный сектор в полярных координатах
65

Пример 4.1. Найти площадь фигуры, ограниченной трехлепестковой розой a cos3
(см. рис. 1.12).
Решение. Найдем сначала площадь половины одного лепестка розы, т.е. 1/6 часть всей площади фигуры:
1 |
|
|
|
1 |
|
/6 |
a cos3 2 d |
1 |
|
/6 |
1 cos6 d |
|
|
|||||||||||||
S |
|
|
|
a2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
6 |
|
|
|
2 |
|
0 |
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a2 |
|
|
|
/ 6 |
|
1 |
sin 6 |
|
/ 6 |
|
|
|
a |
2 |
0 |
|
|
a2 |
2 |
|
||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ед |
|
). |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4 |
|
|
|
|
|
0 |
|
6 |
|
|
0 |
|
|
|
|
4 6 |
|
|
|
24 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: S 4a2 (ед2 ).
Пример 4.2. Найти площадь фигуры, ограниченной лемнискатой Бернулли a cos 2
(см. рис. 1.15).
|
Решение. Найдем сначала площадь одной четверти искомой фигуры, когда меняется от |
|||||||||||||||||||||||
0 до |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/4 |
|
|
2 |
|
|
/6 |
|
|
|
2 |
|
|
|
/ 4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
S |
1 |
a cos 2 |
|
d |
1 |
a2 |
cos 2d |
a |
|
|
1 |
sin 2 |
|
|
|
a |
|
(ед2 ). |
|||
|
|
|
|
|
|
|
|
0 |
|
|
||||||||||||||
|
4 |
|
2 |
0 |
|
|
2 |
|
0 |
|
2 |
|
2 |
|
|
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ответ: S a2 (ед2 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пусть криволинейная трапеция ограничена кривой, заданной параметрически |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x x(t), |
t |
, |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
y y(t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
прямыми x a |
и x b и осью OX, то площадь ее находится по формуле |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S y(t)x (t)dt , |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где и определяются из равенств x( ) a и x( ) b . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Пример 4.3. Найти площадь фигуры, ограниченной эллипсом: |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x a cost, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y bsin t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Найдем сначала 1/4 площади эллипса. Здесь x меняется от 0 до a следовательно, |
|||||||||||||||||||||||
t изменяется от |
|
до 0 (см. рис. 2.2). Находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
66

1 |
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
S |
|
bsin t a cos t |
dt bsin t a sin t dt ab |
sin |
|
tdt |
|
||||||||||||||
4 |
|
||||||||||||||||||||||
|
/2 |
|
|
|
|
/2 |
|
|
|
|
|
|
/2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
1 cos 2t |
|
ab |
|
|
1 |
|
0 |
|
|
ab |
|
2 |
|
|||||
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||
ab |
|
|
dt |
|
|
|
t |
/ 2 |
|
|
sin 2t |
/ 2 |
|
|
|
|
|
(ед |
|
). |
|||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
/2 |
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, площадь эллипса равна S ab (ед2). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример 4.4. Найти площадь фигуры, ограниченной одной аркой циклоиды: |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
x a(t sin t), |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
b(1 cost). |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Изменению t от 0 до 2 |
соответствует изменение x от 0 до |
2 a (см. рис. 2.7). |
||||||||
По формуле: |
|
|
|
|
|
|
|
|
|
|
2 |
|
dt a |
2 |
2 |
2 |
2 |
2 |
dt |
||
S a(1 cos t) a(1 sin t) |
|
(1 cos t) 1 cos t dt a |
|
|
(1 cos t) |
|
||||
0
2
a2
0
2
a2
0
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
1 cos 2t |
|
|
||||
(1 2 cos t cos |
|
t)dt a |
|
1 2 cos t |
|
|
|
dt |
||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
2 |
|
3 |
|
2 |
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 cos t |
|
cos 2t dt a |
|
|
|
t |
|
2sin t |
|
|
|
sin 2t |
||||||
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
0 |
|
|
0 |
|
|
4 |
|
0
2
3 a2 (ед2 ). 0
Задачи и упражнения для самостоятельной работы
4.1. Вычислить площадь фигуры, ограниченной линиями, заданными в полярной системе координат. Фигуру изобразить на чертеже: а) 3cos , 0 2 ; б) 3(1 cos ) , 0 2 ; в) 4 sin 2 ; г) 2 , один виток спирали Архимеда и полярная ось.
4.2. Вычислить площадь фигуры, ограниченной линиями, заданными в параметрической форме. Фигуру изобразить на чертеже: а) x 5cos2 t , y 5sin 2 t ; б) x 3cost , y 3sin t .
4.2. Вычисление длины дуги кривой
Пусть кривая AB задана уравнением в полярных координатах ( ) , где ( ) - непрерывная функция с непрерывной производной при . Тогда длина кривой AB находится по формуле:
|
|
L |
2 ( ) 2 ( )d . |
|
|
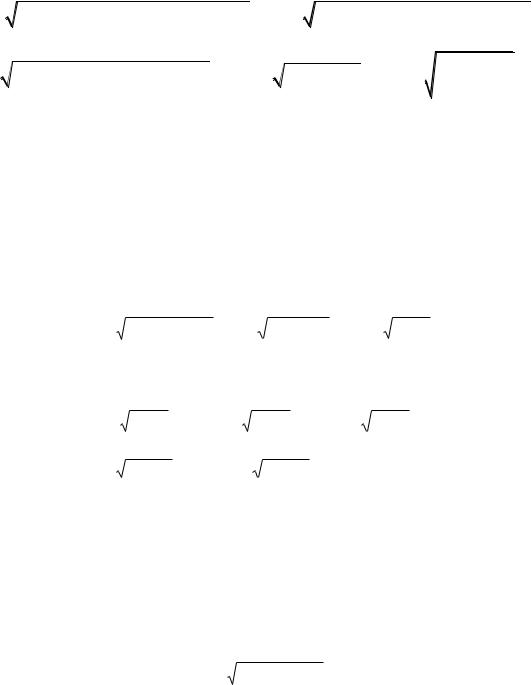
Пример 4.5. Найти длину кардиоиды a(1 cos ) .
Решение. Кардиоида имеет вид, изображенный на рис. 1.19. Она симметрична относительно полярной оси. Найдем половину длины кардиоиды:
67
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
(a(1 cos ))2 |
(a(1 cos )) 2 d |
(a(1 cos ))2 |
(a( sin ))2 d |
||||||||||
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 d |
|
a |
1 2cos cos2 sin2 d a |
|
|
d a |
|
||||||||||
2 2cos |
2 2sin |
||||||||||||||
0 |
|
|
|
|
|
0 |
|
|
0 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a sin d 4a cos |
0 |
4a (ед). |
|
|
|
|
|
|
|
||||||
0 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, длина кардиоиды равна L 8a (ед) . |
|
|
|
||||||||||||
Пример 4.6. Найти длину первого витка архимедовой спирали a .
Решение. Первый виток спирали Архимеда образуется при изменении полярного угла от 0 до 2 (см. рис. 1.20). Тогда
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
a2 2 (a ) 2 d |
|
a2 2 a2 d a |
|
2 1d . |
||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
Используя формулу интегрирования по частям, получим |
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
1 |
|
2 |
|
|
1 |
|
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L a |
|
|
1d a |
|
|
|
|
1 |
|
ln( |
|
|
1) |
|
|
|
|||
|
|
|
|
|
|
|
|||||||||||||
0 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
a |
4 2 |
1 |
1 |
ln( 2 |
4 2 |
1) |
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть кривая AB задана параметрически |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x x(t), |
|
t , |
|
|
|
|
|
|
|||||||
|
|
|
|
|
y(t), |
|
|
|
|
|
|
|
|||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||
где x(t) и y(t) – непрерывные функции с непрерывными производными при t . Тогда длина кривой AB находится по формуле:
|
|
L |
x 2 (t) y 2 (t)dt . |
|
|
Пример 4.7. Найти длину дуги одной арки циклоиды:
x a(t sin t), |
0 |
t 2 . |
|
|
|
||
y a(1 |
cost), |
|
|
Решение. Из уравнения циклоиды находим
x a(1 cost),
y a sin t,
68

когда x пробегает отрезок[0, 2 a], параметр t пробегает отрезок [0, 2 ]. Следовательно, получаем
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
L |
(a(1 cos t))2 (a sin t)2 d a |
1 2 cos t cos2 t sin2 tdt |
|||||||||||||||
0 |
|
|
|
|
|
t |
0 |
|
|
t |
|
t |
|
2 |
|
||
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a |
2 2 cos tdt a |
2 2 sin2 |
|
dt 2a sin |
|
d 4a cos |
|
|
0 |
8a (ед). |
|||||||
2 |
2 |
2 |
|
||||||||||||||
0 |
0 |
|
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x a cos3 t,
Пример 4.8. Найти длину астроиды:
y a sin 3 t.
Решение. Так как кривая симметрична относительно обеих координатных осей, то вычислим сначала длину ее четвертой части, расположенной в первой четверти.
Из уравнения астроиды находим
|
|
|
|
|
x |
3a cos2 t sin t, |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 3a sin 2 t cost. |
|
||||||
Параметр t будет меняться от 0 до / 2 . Следовательно, |
|
|||||||||||
|
1 |
/ 2 |
|
|
|
|
|
|
|
2 |
|
|
L |
9a2 cos4 t sin 2 t 9a2 sin 4 t cos2 td 3a |
cos2 t sin 2 tdt |
||||||||||
4 |
||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
sin 2 t |
|
|
|
3a |
|
|
|
|
|
|
|
|
/ 2 |
|
|
|
||||
3a cost sin tdt |
3a |
|
|
0 |
|
|
, |
|
||||
2 |
|
2 |
|
|||||||||
|
|
0 |
|
|
|
|
|
|
||||
Значит, L 6a (ед). |
|
|
|
|
|
|
|
|
|
|||
Задачи и упражнения для самостоятельной работы
4.3.Вычислить длину дуги кривой, заданной уравнением в полярной системе координат: а)
4 cos ; б) 4(1 cos ) ; в) 5sin ; г) sin 3 3 , 0 t 2 .
4.4.Вычислить площадь фигуры, длину дуги кривой, заданной уравнением в параметриче-
ской форме: а) x 3cost , y 3sin t ; |
б) x 5cos2 t , |
y 5sin 2 t , |
0 t |
|
; |
в) |
|
|
|
|
2 |
|
|
x 2(cost t sin t) , y 2(sin t t cost) , |
0 t . |
|
|
|
|
|
69
ЗАКЛЮЧЕНИЕ
Современную науку невозможно представить без применения графиков. Они стали средством научного анализа и обобщения, а так же являются необходимый элемент в практической и исследовательской работе инженерно-технических специалистов. Поэтому так важно понимать и хорошо владеть техникой построения графиков функций в разных системах координат.
Предлагаемое учебное пособие позволит учащимся разобраться с основными понятиями построения функций, заданных параметрическим образом и в полярной системе координат.
Эти знания, безусловно, помогут Вам при изучении таких разделов как аналитическая геометрия, приложение определенных и кратных интегралов к задачам геометрии и механики, дифференциальное исчисление функции одной переменной и др. В качестве справочного материала может быть использовано при выполнении курсовых и дипломных проектов.
Авторы надеются, что данное пособие будет хорошим подспорьем для студентов, как во время аудиторных занятий, так и в процессе самостоятельной работы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Берман Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман. – М.: Наука.
–2003 г. – 416 с.
2. Бронштейн И.П. Справочник по математике / И.П. Бронштейн, К.А. Семендяев. – М.:
Наука, 1986. – 345 c.
3. Выгодский М.Я. Справочник по элементарной математике / М.Я. Выгодский. – М.: ООО
«Изд-во АСТ», 2003. – 509 с.
4. Выгодский М.Я. Справочник по высшей математике / М.Я. Выгодский. – М.: ООО «Издво Астрель»: «Изд-во АСТ», 2003. – 499 с.
5. Грибов А.Ф. Построение кривых, заданных параметрически и в полярной системе координат: Методические указания / А.Ф. Грибов, А.В. Котович, О.М. Минеева. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 31 с.
6. Данко П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Выс. шк., 2000. – 255 с.
7. Клетеник Д.В. Сборник задач по аналитической геометрии / Д.В. Клетеник. – М.: Наука,
1980. – 240 с.
8. Микуцкая Г.С. Построение кривых и поверхностей / Г.С. Микуцкая, В.Н. Стефанова,
Г.Г.Судакова. – Л.: ЛКИ, 1992. – 105 с.
9. Минорский, В.П. Сборник задач по высшей математике / В.П. Минорский. – М.: Наука,
1987. – 287 c.
10. Привалов И.И. Аналитическая геометрия: учебник / И.И. Привалов.– СПб.: Изд-во
«Лань», 2004. – 304 c.
11. Пискунов Н.С. Дифференциальное и интегральное исчисление / Н.С Пискунов. – М.:
Наука, 2003. – 309 c.
12. Соболев С.К. Исследование и построение плоских кривых, заданных параметрически и в полярных координатах / С.К. Соболев, А.Т. Ильичев. – М.: Изд-во МГТУ им. Н.Э. Баумана,
2004. – 78 с.
13. Райхмист Р.Б. Графики функций / Р.Б. Райхмист. – М.: Высшая школа, 1991. – 151 с. 14. Шипачев В.С. Высшая математика / В.С. Шипачев. – М.: Высшая школа, 2003. – 425 c.
70
