
3007
.pdf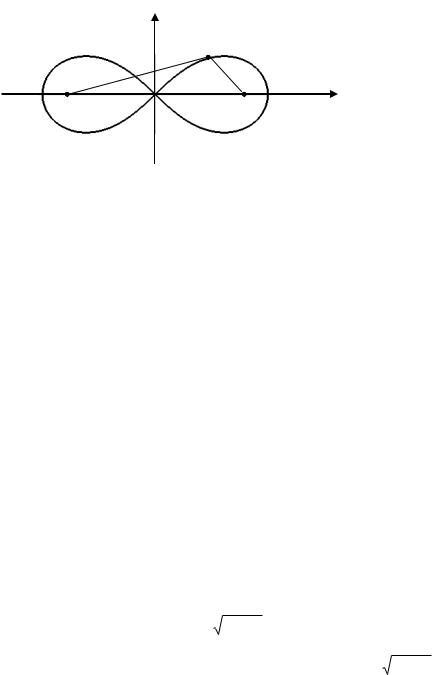
Y
M(x,y)
F1( a,0) |
0 |
F (a,0) |
X |
|
|
|
|
Рис. |
1.15. Лемниската Бернулли |
|
Итак, |
лемниската Бернулли, имеющая уравнение 2 |
2a2 cos 2 в полярных координатах |
|
и x2 y2 2 |
2a2 x2 y2 в декартовых координатах, является геометрическим местом точек, |
||
произведение расстояний которых до двух данных точек |
F (a,0) и F1( a,0) есть величина по- |
||
стоянная, равная a2 . |
|
||
Лемниската Бернулли симметрична относительно начала координат, которое является узловой точкой с касательными y x и точкой перегиба. Площадь каждой петли S a2 . Лемни-
ската Бернулли названа по имени Я. Бернулли, в статье которого впервые встречается уравнение этой кривой (1694 г.).
Пример 1.15. Дано полярное |
уравнение лемнискаты Бернулли 2 |
9sin 2 . Построить |
||||||||||||||||
эту линию по точкам, придавая углу |
значения с шагом |
|
. Найти декартово уравнение за- |
|||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
||
данной кривой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Поскольку левая часть данного уравнения неотрицательна, то угол может из- |
||||||||||||||||||
меняться только в тех пределах, для которых sin 2 0 , то есть |
0 |
|
и |
3 |
. Для |
|||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
вычисления значений с точностью 0,01, составим табл. 1.3. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.3 |
|||
|
|
|
|
|
Значения функции 3 sin 2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
sin 2 |
|
|
|
3 sin 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
0,5 |
|
|
|
|
2,12 |
|
|
|
|||
12 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0,87 |
|
|
|
2,79 |
|
|
|
|||||
6 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
||||
4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
0,87 |
|
|
|
2,79 |
|
|
|
|||||
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
5 |
|
|
5 |
|
|
0,5 |
|
|
|
|
2,12 |
|
|
|
|||
12 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
21
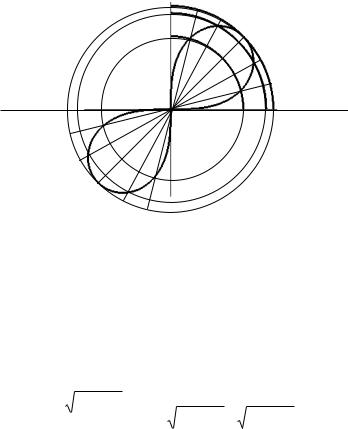
При изменении угла в пределах III четверти будет принимать те же значения, что и в I четверти. Поэтому линия будет расположена симметрично относительно начала координат. Для ее построения проводим из полюса лучи, соответствующие выбранным значениям , и на каж-
дом луче откладываем найденные значения полярного радиуса. Полученные точки соединяем плавной линией (рис. 1.16).
|
|
5 /12 |
|
|
|
/ 3 |
|
|
|
/ 4 |
|
|
|
/ 6 |
|
|
|
/12 |
|
|
|
0, |
2 |
|
|
|
|
13 /12 |
|
|
|
7 / 6 |
|
|
|
5 / 4 |
|
|
|
4 / 3 |
17 /12 |
|
|
|
|
||
Рис. 1.16. Построение лемнискаты Бернулли |
|||
с использованием полярной сетки |
|
||
Найдем уравнение лемнискаты |
Бернулли в декартовых |
координатах. Так как |
|
2 9sin 2 9 2 sin cos 18sin cos , то, используя формулы (1.1) и (1.2) перехода к де-
картовых координатам, получим |
|
|
|
|
|
|
|
|
|
|
x2 y2 2 18 |
|
|
y |
|
x |
, |
||
x2 |
y2 |
x2 y2 |
|||||||
|
|
|
|
|
|||||
|
x2 y2 |
|
18xy |
|
|
. |
|
||
|
x2 y2 |
|
|||||||
|
|
|
|
|
|||||
Окончательно имеем
x2 y2 2 18xy .
1.3.3. Кардиоида
Плоские кривые, представляющие траектории точки окружности, катящейся по другой окружности и имеющей с ней внешнее касание, называются эпициклоидами. В зависимости от величины отношения m R / r ( r и R – радиусы катящейся и неподвижной окружностей соответственно), получаются эпициклоиды различной формы. При m 1 эпициклоида называется кар-
22

диоидой. Рассмотрим пример, позволяющий более подробно рассмотреть эту кривую.
Пример 1.16. Окружность диаметра а катится без скольжения по внешней стороне другой, неподвижной окружности такого же диаметра. В полярной системе координат составить уравнение линии, описанной некоторой фиксированной точкой катящейся окружности.
Решение. Пусть на плоскости дана некоторая точка O (полюс) и проходящая через нее ось O (полярная ось), а также указана единица масштаба. Построим окружность диаметра а с
центром в точке C2 (рис. 1.17). Это неподвижная окружность, по ней катится без скольжения окружность такого же диаметра с центром в точке C1, оставаясь, все время вне неподвижной окружности. Траектория некоторой точки M окружности катящегося круга называется кардиои-
дой.
Пусть A – первоначальное положение точки, описывающей искомую линию (точка A диаметрально противоположна точке B, где в начальный момент соприкасаются окружности); M – новое положение точки A, описывающей искомую линию. После перемещения окружности C1 в положение C3 точка P займет положение D, причем, поскольку качение происходит без скольжения, длина дуги BQ равна длине дуги DQ, QC2 B QC3D . На рис. 1.17 ось OX совмещена с
полярной осью O , полюс – с началом координат. Требуется составить уравнение, которому удовлетворяют координаты любой точки M ( , ) искомой линии.
M
|
С3 |
C3 |
|
|
|
D |
|
|
|
Q |
|
|
|
P |
|
С |
|
|
|
|
2 |
B |
A |
|
|
||
O |
C2 |
C1 |
X , |
Рис. 1.17. Геометрические построения к выводу уравнения кардиоиды
Угол MC3Q равен углу OC2Q , в силу чего четырехугольник OC2C3M является равнобед-
ренной трапецией с меньшим основанием C C a ; |
C C и |
C C – перпендикуляры, опущен- |
|||||||||
|
|
|
2 |
3 |
|
|
2 |
2 |
3 |
3 |
|
ные из точек C2 и C3 на прямую OM. Так как R a / 2 , – полярный угол то |
|||||||||||
OM OC |
C C |
C M |
a |
cos a |
a |
cos a(1 cos ) . |
|||||
|
|
||||||||||
2 |
2 |
3 |
3 |
2 |
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
||||
Таким образом, уравнение искомой линии в полярных координатах принимает вид |
|||||||||||
|
|
|
|
a(1 cos ) , |
|
|
(1.13) |
||||
а соответствующая ему кривая является кардиоидой (рис. 1.18).
23

Y
M
y
0 x N X ,
Рис. 1.18. Кардиоида a(1 cos )
Поскольку при замене на уравнение кардиоиды не меняется, то кардиоида распо-
ложена симметрично относительно полярной оси. Если изменять от 0 |
до , то бу- |
|||||||
дет убывать от 2a |
до 0 . |
|
|
|
|
|
|
|
Если в уравнении a(1 cos ) перейти от полярных координат к декартовым, то по- |
||||||||
лучим |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x2 y2 a 1 |
|
|
|
, |
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
x |
2 |
y |
2 |
|
|
|
|
|
|
|
|
|
||
|
x2 y2 a |
x2 y2 x , |
|
|||||
|
x2 y2 ax a x2 y2 , |
|
||||||
|
x2 y2 ax 2 a2 x2 a2 y2 , |
|
||||||
|
x2 y2 ax 2 a2 x2 a2 y2 , |
|
||||||
|
x2 y2 ax ax x2 y2 ax ax a2 y2 , |
|
||||||
|
x2 y2 2ax x2 |
y2 a2 y2 |
0 . |
(1.14) |
||||
Полученное уравнение кардиоиды в декартовых координатах весьма сложно, поэтому для построения этой кривой удобнее всего использовать уравнение в полярных координатах
a(1 cos ) .
Пример 1.17. Построить кривую, заданную уравнением в полярных координатах
a(1 cos ) .
Решение. Заданная кривая также называется кардиоидой. Для ее построения используем тот факт, что при замене на , (в силу четности косинуса) уравнение не изменится, то есть кривая будет симметрична относительно полярной оси. Поэтому таблицу значений для функции
24
( ) a(1 cos ) достаточно составить для 0 , а затем отобразить эту часть графика на интервал 2 . Для удобства построения составим табл. 1.4.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.4 |
|
|
|
Значения функции a(1 cos ) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
2 |
|
3 |
|
5 |
|
|
|||
6 |
4 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
4 |
|
6 |
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
cos |
1 |
0,87 |
0,7 |
0,5 |
0 |
-0,5 |
-0,7 |
-0,87 |
-1 |
|
||||||
a(1 cos ) |
0 |
0,13a |
0,3a |
0,5a |
a |
1,5a |
1,7a |
1,87a |
a |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
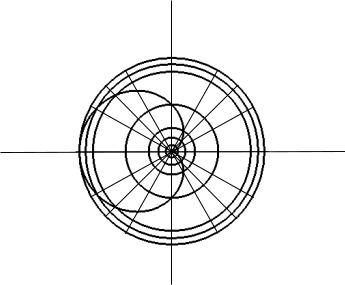
Точки с координатами, заданными таблицей, строим в полярной системе координат, используя полярную сетку (см. пример 1.13). Соединив полученные точки плавной линией, получим заданную кривую (рис. 1.19).
/ 2
2 / 3 |
/ 3 |
3 / 4 |
/ 4 |
5 / 6 |
/ 6 |
|
|
|
0, 2 |
Рис. 1.19. Построение кардиоиды a(1 cos ) с использованием полярной сетки
Задачи и упражнения для самостоятельной работы
1.9.Построить кривые: а) sin 3 ; б) cos2 ; в) 2(1 cos ) .
1.10.Построить кривые: а) 2 cos ; б) 3 2sin 2 ; в) 2 sin 3 .
1.4. Спирали
Спиралями называются плоские кривые, которые обходят вокруг одной или нескольких точек, приближаясь или удаляясь от них. Алгебраические спирали – спирали, уравнения которых в полярных координатах являются алгебраическими относительно переменных и . Далее подробно рассмотрим следующие алгебраические спирали: спираль Архимеда, гиперболи-
25

ческую спираль, спираль Галилея, спираль Ферма, параболическую спираль, жезл, а также логарифмическую спираль.
1.4.1. Спираль Архимеда
Спираль Архимеда представляет собой путь, описываемый некоторой точкой, движущейся с постоянной скоростью v по лучу, вращающемуся около полюса O с постоянной угловой ско-
ростью . Ее уравнение в полярных координатах a , где a v , . Для доказа-
тельства рассмотрим следующий пример.
Пример 1.18. Точка М равномерно перемещается по лучу, вращающемуся равномерно около полюса. Составить уравнение линии, описанной точкой М, если в начальный момент вращающийся луч совпадает с полярной осью, точка М – с полюсом, а при повороте луча на угол 1 (один радиан) точка М удалилась от полюса на расстояние а.
Решение. Так как в начальный момент и равны нулю, а затем оба возрастают про-
порционально времени, то они связаны прямой пропорциональной зависимостью const. Но
при 1, |
a , следовательно, |
|
|
a |
, то есть |
|
|
|
|
||||
|
|
1 |
|
|
||
|
|
|
|
|
a . |
(1.15) |
Получили уравнение кривой – спирали Архимеда. В декартовых координатах уравнение имеет вид
x2 y2 |
a arctg |
y |
. |
(1.16) |
|
||||
|
|
x |
|
|
Пример 1.19. Построить спираль Архимеда, заданную уравнением 12 .
Решение. Составим табл. 1.5 значений функции ( ) 12 .
Таблица 1.5
Полярные координаты точек спирали Архимеда 12
Точки |
М1 |
|
М2 |
|
М3 |
|
|
М4 |
|
|
М5 |
|
|
М6 |
|
|
М7 |
|
|
М8 |
М9 |
|
||||||||
|
0 |
|
|
|
|
|
|
3 |
|
|
|
|
|
5 |
|
|
|
3 |
|
|
|
7 |
|
2 |
|
|||||
|
4 |
|
2 |
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0,4 |
|
0,8 |
|
3 |
|
1,2 |
|
1,6 |
|
5 |
2 |
|
3 |
2,4 |
|
7 |
2,8 |
3,14 |
|
||||||||
0 |
8 |
4 |
|
8 |
2 |
|
8 |
|
|
4 |
|
|
8 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
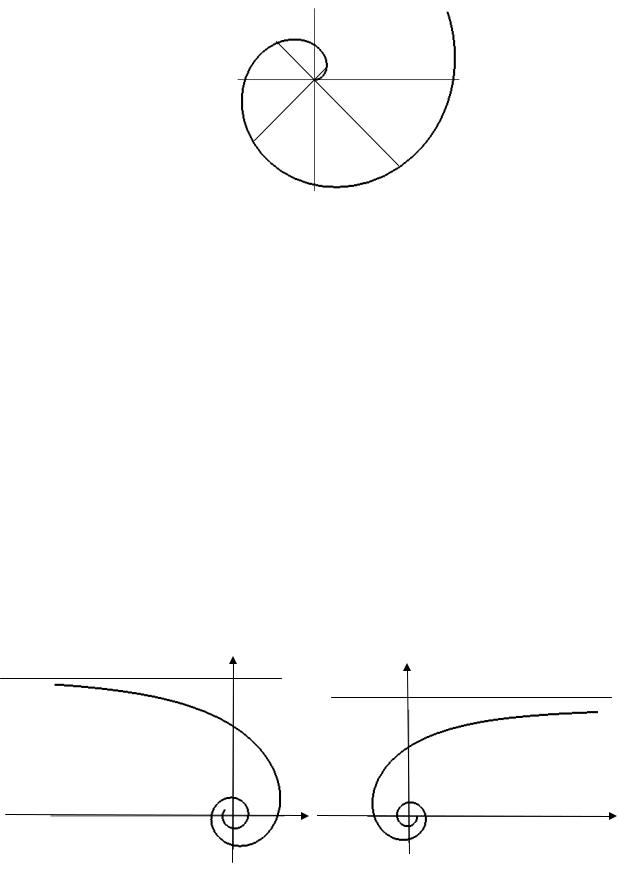
Полученные из табл. 1.5 точки М1, |
М2, ..., М9 |
соединим плавной линией. На рис. 1.20 при- |
||||||||||||||||||||||||||||
веден один виток спирали Архимеда.
26
|
М4 |
М3 |
|
|
|
|
|
М5 |
|
М2 |
М9 |
|
|
М1 |
|
М6
М8
М7
Рис. 1.20. Спираль Архимеда
1.4.2. Гиперболические спирали
Гиперболические спирали состоят из двух ветвей, расположенных симметрично относительно оси OY. В полярных координатах уравнение первой ветви
|
|
|
|
|
a |
, |
; |
(1.17′) |
|
|
|
|
|||||||
|
|
|
|||||||
|
|||||||||
уравнения второй ветви |
|
|
|
|
|
||||
|
a |
, |
0 . |
(1.17″) |
|||||
|
|||||||||
|
|
|
|
|
|
||||
График гиперболических спиралей представлен на рис. 1.21, где совмещены полярная ось с положительной полуосью ОХ, а полюс – с началом координат. Для обеих ветвей прямая y a
будет асимптотой, так как, например, если |
y sin и |
a |
, то |
при |
0 |
||||
|
|||||||||
|
|
|
|
|
|
|
|
||
lim |
y lim sin lim |
a |
sin |
a lim |
sin |
a . |
|||
|
|
||||||||
0 |
0 |
0 |
|
|
0 |
|
|||
Отметим, что точка О – асимптотическая точка при |
и |
. |
|||||||
а) |
|
б) |
|
|
|
|
|
|
|
y a |
Y |
|
|
Y |
|
|
|
|
|
y a
0 |
0 |
|
|
X, |
X, |
Рис. 1.21. Две ветви гиперболической спирали:
а) |
|
a |
, ; |
б) |
a |
, 0 |
|
|
|
||||
|
|
|
|
|
||
27
|
|
|
|
1.4.3. Спираль Галилея |
|
|
|
|
|
||||
|
Полярное уравнение спирали Галилея имеет вид |
|
|
|
|
|
|
||||||
|
|
|
|
a 2 |
l , |
l 0 . |
|
|
|
|
(1.18) |
||
|
Кривая симметрична |
относительно |
полярной |
оси. Если |
0 , то |
l , |
а если |
||||||
|
l / a , то 0 . Таким образом, кривая имеет двойную точку в полюсе (рис. 1.22). А также |
||||||||||||
бесконечное множество |
двойных точек |
на полярной оси, для |
которых |
a k |
2 |
l , где |
|||||||
k k , k 1, 2, 3,... . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При l 0 получаем спираль a 2 , полюс которой является особой точкой (если 0 , |
||||||||||||
то 0 и производная 0 ), причем |
|
|
|
|
|
|
|
|
|
||||
|
lim |
y |
lim |
sin |
cos |
|
lim |
2a sin a 2 cos |
0 . |
|
|
||
|
cos |
sin |
2a cos a 2 sin |
|
|
||||||||
|
0 |
x |
0 |
0 |
|
|
|
|
|||||
0 |
X, |
Рис. 1.22. Спираль Галилея a 2 l , l 0 .
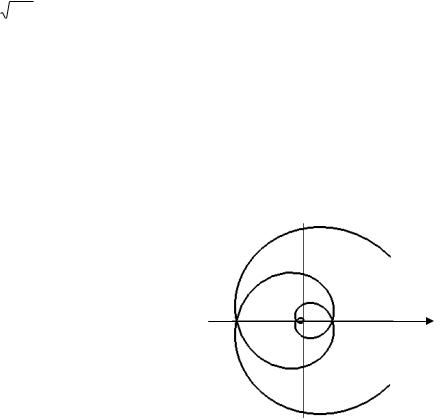
1.4.4. Спираль Ферма
Спираль Ферма (рис. 1.23) – плоская кривая, уравнение которой в полярных координатах имеет вид
2 a2 . |
(1.19) |
Спираль относится к типу алгебраических спиралей. Каждому значению соответствует два значения – положительное и отрицательное. Спираль Ферма центрально симметрична относительно полюса, который является точкой перегиба.
28
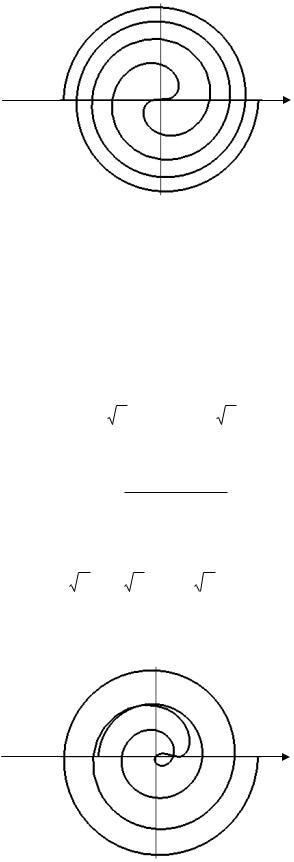
0
Рис. 1.23. Спираль Ферма 2 a2
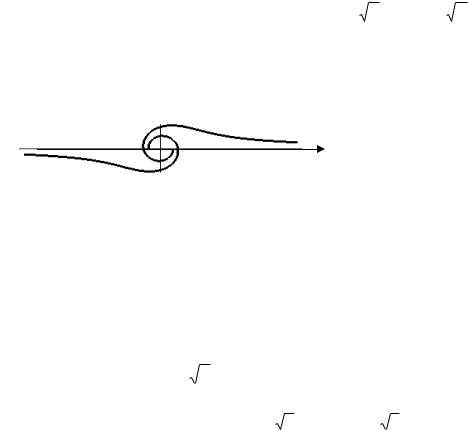
1.4.5. Параболическая спираль
Параболическая спираль представляет собой плоскую кривую, уравнение которой в полярных координатах имеет вид
l 2 a2 , |
l 0 . |
(1.20) |
Кривая состоит из двух ветвей: a l и a l . Вторая из них образует с пер-
вой бесконечное множество двойных точек. Кривая имеет также одну точку перегиба (рис. 1.24). Действительно, касательная и кривая в точке 0 совпадает с полярной осью, а кривизна
K2 2 2 3 / 2
2 2
обращается в нуль при 1 , где 1 0 – корень уравнения
4 l a 2 3a2 |
al 0 . |
Если l 0 , то кривая (1.20) становится спиралью Ферма (см. рис. 1.23).
0 |
|
Рис. 1.24. Параболическая спираль l 2 a2 , |
l 0 |
29
|
|
1.4.6. Жезл |
|
|
|
|
|
||
Полярное уравнение жезла имеет вид |
|
|
|
|
|
|
|
|
|
2 |
|
a2 |
. |
|
|
(1.21) |
|||
|
|
|
|||||||
|
|
|
|
|
|
|
|
||
Кривая обладает центральной симметрией и состоит из двух ветвей |
a |
и |
|
a |
, |
||||
|
|
||||||||
|
|
|
|
|
|
|
|||
каждая из которых асимптотически приближается к полюсу (рис. 1.25).
|
|
Рис. 1.25. Жезл |
2 |
a2 |
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
Если 0 , то ; поскольку |
|
|
|
|
|
|
|
|
|
||
|
|
lim |
sin lim |
a sin |
0 |
, |
|
|
|||
|
|
|
|
|
|||||||
|
|
0 |
0 |
|
|
|
|
||||
то полярная ось служит асимптотой данной кривой. Так как кривизна линии K 0 |
при 1/ 2 , |
||||||||||
причем K 0 при 1/ 2 |
и K 0 |
при 0 1/ 2 , то точки 1/ 2; a |
2 и 1/ 2; a |
2 являются |
|||||||
точками перегиба.
1.4.7. Логарифмические спирали
Линия, задаваемая в полярных координатах уравнением
aek , |
(1.22) |
где a и k – положительные постоянные, называется логарифмической спиралью.
Пример 1.20. Требуется построить график логарифмической спирали 2ek .
Решение. Придавая различные значения ( ) и определяя соответствующие значения , можно найти множество значений , , удовлетворяющих данному уравнению. Сначала определим значения по выбранным значениям из интервала и составим соответствующую табл. 1.6. Как видно из этой таблицы, при возрастании угла в арифметиче-
ской прогрессии с разностью 2 полярный радиус возрастает в геометрической прогрессии со
30
