
3007
.pdf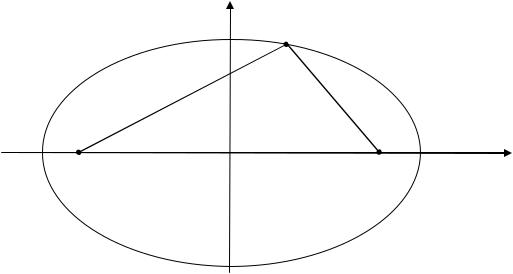
2. Точки пересечения с осями координат. Положив y 0 в уравнении (3.4), находим две точки A1 ( a,0) и A2 (a,0) , в которых эллипс пересекает ось OX. Положив x 0 , находим точки пересечения эллипса с осью OY: B1 (0, b) и B2 (0, b) .
Точки A1 , A2 , B1 , B2 называются вершинами эллипса. Отрезки A1A2 и B1B2 , а также их
длины 2а и 2b называются соответственно большой и малой осями эллипса. Числа а и b назы-
ваются соответственно большой и малой полуосями эллипса.
3. Форма эллипса. Из уравнения (3.4) следует, что каждое слагаемое в левой части не пре-
восходит |
единицы, |
то есть |
имеют место неравенства |
x2 |
1 и |
y2 |
1 или |
a x a |
и |
||||
|
|
||||||||||||
|
|
|
|
а2 |
b2 |
|
|
|
|
|
|
||
b y b . Следовательно, |
все точки эллипса лежат внутри прямоугольника, |
образованного |
|||||||||||
прямыми |
x a и |
y b . В уравнении (3.4) сумма неотрицательных слагаемых |
x2 |
и |
|
y2 |
|
||||||
|
|
|
|
|
|
|
|
|
а 2 |
b2 |
|||
равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться. Например, с увеличением x от 0 до а переменная y уменьшается от b до 0.
Таким образом, эллипс имеет форму, изображенную на рис. 3.3.
Y
B2(0,b) M(x,y
A1(-a,0) |
F1(-c,0) |
0 |
F2(c,0) A2(a,0) X |
|
|
|
|
B1(0,-b) |
|||
Рис. 3.3. Эллипс |
|
x2 |
|
y2 |
1 , a b |
||
|
а2 |
|
|||||
|
|
|
|
b2 |
|||
3.2.3. Эксцентриситет и директрисы эллипса |
|||||||
Форма эллипса зависит от отношения |
b |
. Например, при a b эллипс превращается в |
|||||
a |
|||||||
|
|
|
|
|
|
||
окружность с уравнением |
x2 y2 a2 . В качестве характеристики формы эллипса принято ис- |
|||||
пользовать отношение |
с |
, |
которое называют эксцентриситетом эллипса и обозначают |
|
||
a |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
с |
, |
(3.5) |
|
|
|
|
|||
|
|
|
|
a |
|
|
51
причем 0 1, так как 0 с а . С учетом формулы (3.3) формулу (3.5) можно переписать в виде
|
а2 |
b2 |
|
|
а2 b2 |
|
1 |
b2 |
, |
||
a |
а2 |
а2 |
|||||||||
|
|
|
|
|
|||||||
То есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
1 2 . |
|
|
|
|
||
|
|
|
а |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Очевидно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным, а если положить 0 , то эллипс превращается в окружность.
Пусть M (x, y) – произвольная точка эллипса с фокусами F1 и F2 (рис. 3.4). Длины отрезков F1M r1 и F2M r2 называются фокальными радиусами точки М. Очевидно,
r1 r2 2а .
и имеют место формулы
|
|
r1 а х и r2 а х . |
|
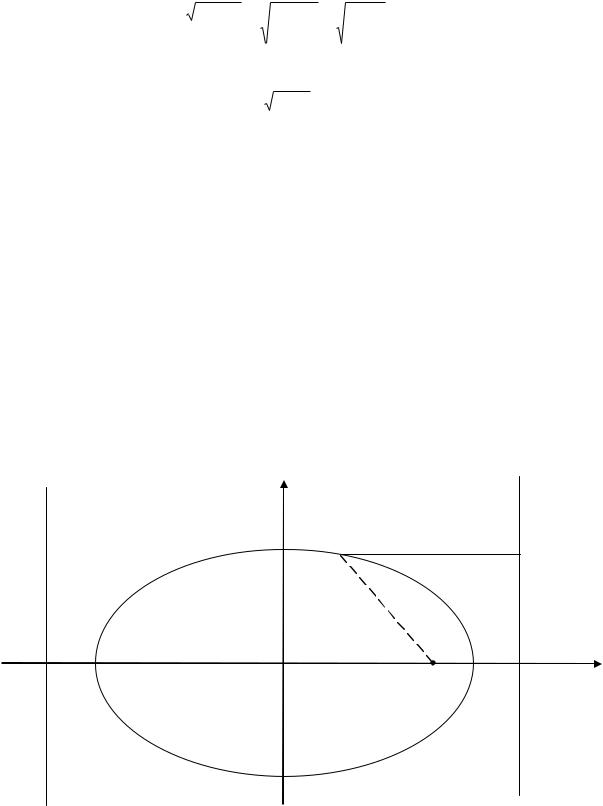
Прямые x |
a |
называются директрисами эллипса. Эти прямые обладают следующим |
|
|
|||
|
|
свойством: отношение расстояний любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равная .
Y
M(x,y)
x |
a |
|
|
x |
a |
|
|
|
|
||||
|
|
|
||||
0 |
F2(c,0) |
|
|
X |
||
Рис. 3.4. Директрисы эллипса
52
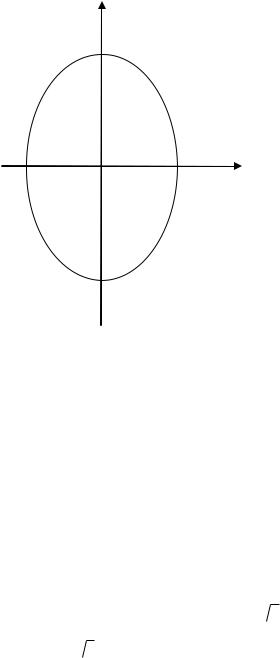
Из равенства (3.3) следует, что a b . Если же a b , то уравнение (3.4) определяет эллипс, большая ось которого 2b лежит на оси OY, а малая ось 2a – на оси OX (рис. 3.5). Фокусы такого
эллипса находятся в точках F1(0,-с) и F2(0,с), где b2 а2 с2 .
Y
 F2(0,с)
F2(0,с)
0 |
X |
 F1(0,-с)
F1(0,-с)
Рис. 3.5. Эллипс |
x2 |
|
y2 |
1 , a b |
|
а2 |
b2 |
||||
|
|
|
Задачи и упражнения для самостоятельной работы
3.3. Составить каноническое уравнение эллипса, найти координаты фокусов. Изобразить кривую, если:
а) его полуоси соответственно равны 4 и 3; б) расстояние между фокусами равно 8, а большая ось равна 10;
в) малая полуось равна 2, расстояние между фокусами равно 6; г) большая полуось равна 10 и эксцентриситет равен 0,6; д) малая полуось равна 6 и эксцентриситет равен 0,8;
е) эксцентриситет равен 0,8 и расстояние между фокусами равно 8; ж) сумма полуосей равна 10 и расстояние между фокусами равно 4 5 .
5 .
3.4.Эллипс проходит через точки М (2,  3) и B(0,2) . Написать его уравнение, найти расстояние от точки М до его фокусов. Сделать чертеж.
3) и B(0,2) . Написать его уравнение, найти расстояние от точки М до его фокусов. Сделать чертеж.
3.5.Найти длины осей, координаты фокусов и эксцентриситет эллипса, заданного уравне-
нием:
а) 9x2 25y2 225 ; б) 25x2 16 y2 400 .
3.6. Составить уравнение линии, каждая точка M (x, y) которой отстоит от точки F(-1,0) на расстоянии вдвое меньшем, чем до прямой x= -4.
53

3.3.Гипербола
3.3.1.Каноническое уравнение гиперболы
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Обозначим фокусы через F1 и F2 , расстояние между ними 2с , а модуль разности расстояний от произвольной точки гиперболы до фокусов – через 2а . По определению 2а 2c . Для вывода уравнения гиперболы выберем систему координат OXY так, чтобы фокусы F1 и F2 лежали на оси OX, а начало координат совпадало с серединой отрезка F1F2 . Тогда фокусы будут иметь следующие координаты F1(-c,0) и F2(c,0) .
Пусть M (x, y) – произвольная точка гиперболы. Тогда, согласно определению гиперболы, MF1 MF2 2а , то есть
(x с)2 y2 (x с)2 y2 2а .
После преобразований, аналогичных случаю вывода уравнения эллипса, получим канони-
ческое уравнение гиперболы |
|
|
|
|
||
|
x2 |
|
|
y2 |
1. |
(3.6) |
|
а2 |
b2 |
||||
|
|
|
|
|||
где |
|
|
|
|
||
|
b2 |
с2 |
а2 . |
(3.7) |
||
3.3.2. Исследование формы гиперболы
Установим форму гиперболы, пользуясь ее каноническим уравнением (3.6).
1.Симметрия гиперболы. Уравнение (3.6) содержит x и y только в четных степенях, следовательно, гипербола симметрична относительно координатных осей и начала координат. Точку
O(0,0) называют центром симметрии гиперболы.
2.Точки пересечения с осями координат. Положив y 0 в уравнении (3.6), находим две точки пересечения гиперболы с осью OX: A1 (a, 0) и A2 (a, 0) . Положив x 0 в уравнении
(3.6), получим y2 b2 , такое уравнение решений не имеет. Следовательно, гипербола ось OY не пересекает.
Точки A1 , A2 называются вершинами гиперболы. Отрезок A1A2 = 2а называют действи-
тельной осью, а число а – действительной полуосью гиперболы. Отрезок B1B2 = 2b называют
мнимой осью, а число b – мнимой полуосью гиперболы.
Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы. 3. Форма гиперболы. Так как гипербола симметрична относительно начала координат, то
исследовать ее форму достаточно при x 0 и |
y 0 . Из уравнения (3.6) следует, что |
x2 |
1, то |
|
а2 |
||||
|
|
|
есть x a . |
Это означает, что точки кривой расположены справа от прямой x a (правая ветвь |
гиперболы). |
Аналогично, слева от прямой x a располагается левая ветвь гиперболы. Из |
54
уравнения (3.6) видно, что когда x возрастает, то и y тоже возрастает, так как разность x2 y2
а2 b2
сохраняет постоянное значение, равное единице.
4. Асимптоты гиперболы.
Прямая L называется асимптотой неограниченной кривой K, если расстояние от точки M кривой K до этой прямой стремится к нулю при неограниченном удалении точки M вдоль кривой K от начала координат.
Гипербола |
x2 |
|
y2 |
1 имеет две асимптоты: |
||||||
а2 |
b2 |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
y |
b |
x и |
y |
b |
x . |
|
|
|
|
|
|
а |
|
а |
|||
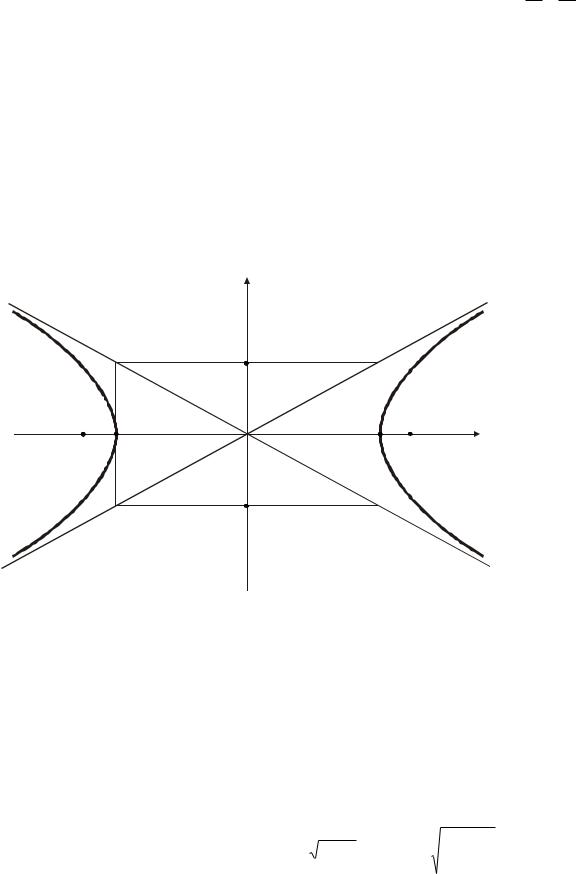
Таким образом, гипербола имеет форму, изображенную на рис. 3.6.
|
|
|
Y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
B2(0,b) |
|
||
|
|
|
|
|
|
|
|
|
|
-a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
F1(-c,0) |
A1(-a,0) |
O |
|
|
A2(a,0) |
F2(c,0) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1(0,-b) |
|
||
-b
(3.8)
x
X
Рис. 3.6. Гипербола |
x2 |
|
y2 |
1 |
|
а2 |
b2 |
||||
|
|
|
3.3.3. Эксцентриситет и директрисы гиперболы
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к величине действительной оси гиперболы,
|
|
|
|
|
|
|
|
с |
. |
|
|
|
|
|
|
|
|
(3.9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
Так как с а , то 1. Эксцентриситет характеризует форму гиперболы. Действительно, |
|||||||||||||||||||
|
b2 |
|
с2 |
|
|
|
b |
|
|
2 |
|
|
|
b 2 |
|||||
из равенства (3.7) следует, что |
|
|
|
|
|
1 |
, то есть |
|
|
|
|
1 |
и |
|
1 |
|
. |
||
|
2 |
|
2 |
|
|
|
|||||||||||||
|
а |
|
|
а |
|
|
|
|
|
а |
|
|
|
|
|
|
|
а |
|
55
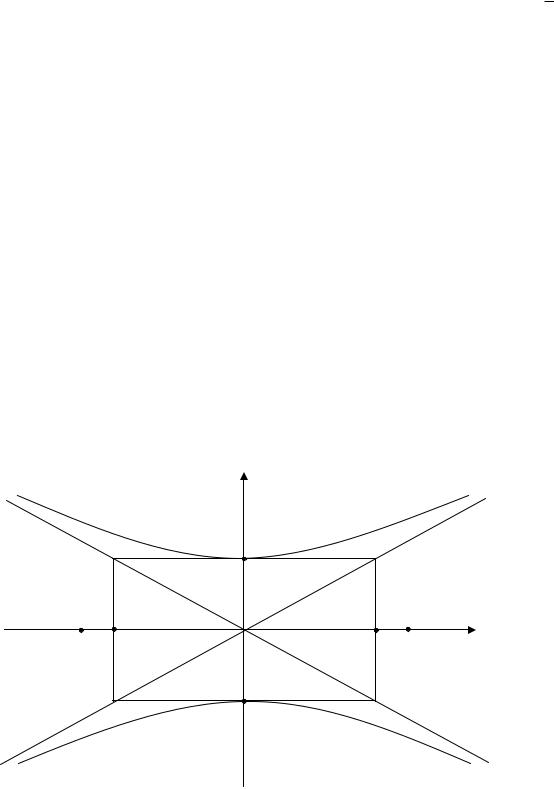
Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение
полуосей, а значит, тем более вытянут ее основной прямоугольник.
Фокальные радиусы точки М, принадлежащей правой ветви гиперболы имеют вид:
r1 х а и r2 х а ,
в случае левой ветви:
r1 ( х а) и r2 ( х а) .
b ее
а
Прямые x |
a |
называются директрисами гиперболы. Так как 1, |
то |
a |
a . Значит, |
|
|
|
|||||
|
|
|
|
что правая директриса расположена между центром и правой вершиной гиперболы, а левая ‒ между центром и левой вершиной гиперболы.
Директрисы гиперболы имеют то же свойство, что и директрисы эллипса: отношение рас-
стояний любой точки гиперболы до фокуса и соответствующей директрисы есть величина постоянная, равная .
3.3.4. Различные виды гиперболы
Гипербола называется равносторонней, если ее полуоси равны а b . Ее каноническое уравнение имеет вид:
x2 y2 а2 .
Асимптоты равносторонней гиперболы имеют уравнения: y x и y x .
Y
B2(0,b)
|
|
|
|
|
|
|
|
F1(-c,0) |
A1(-a,0) |
O |
A2(a,0) |
F2(c,0) |
X |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
B1(0,-b)
Рис. 3.7. Сопряженные гиперболы |
y2 |
|
x2 |
1 и |
x2 |
|
y2 |
1 |
|
b2 |
а2 |
а2 |
b2 |
||||||
|
|
|
|
|
56
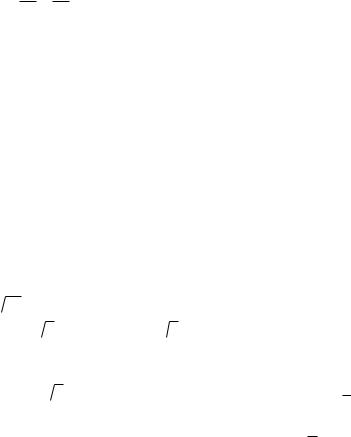
Кривая, определяемая уравнением
y2 x2 1
b2 а2
также является гиперболой, действительная ось которой 2b расположена на оси ординат, а мни-
мая 2а – на оси абсцисс. Эта гипербола изображена на рис. 3.7. Гиперболы |
y2 |
|
x2 |
1 и |
|||||
b2 |
а2 |
||||||||
|
|
|
|
|
|
|
|||
|
x2 |
|
y2 |
1 имеют общие асимптоты и называются сопряженными. |
|
|
|
|
|
|
а2 |
b2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Задачи и упражнения для самостоятельной работы
3.7. Составить каноническое уравнение гиперболы, найти координаты фокусов. Изобразить кривую, если:
а) его полуоси соответственно равны 4 и 3; б) расстояние между фокусами равно 14, а расстояние между вершинами 12;
в) действительная полуось равна 5, эксцентриситет равен 1,4; г) расстояние между фокусами равно 16 и эксцентриситет равен 4/3;
д) действительная полуось равна  15 и гипербола проходит через точку (5, 2) ; е) гипербола проходит через точки М (2
15 и гипербола проходит через точку (5, 2) ; е) гипербола проходит через точки М (2 7, 3) и N ( 7, 6
7, 3) и N ( 7, 6 32) .
32) .
3.8. Составить каноническое уравнение гиперболы. Изобразить кривую, если:
а) гипербола проходит через точку (10, 3 3) , асимптоты заданы уравнениями y 53 x ;
3) , асимптоты заданы уравнениями y 53 x ;
б) расстояние между фокусами равно 10, асимптоты заданы уравнениями y 12 x .
3.9. Найти длины осей, координаты фокусов и эксцентриситет гиперболы, заданной уравнением:
а) 25x2 144 y2 3600 ; б) 16 y2 9x2 144 .
3.10. Составить уравнение линии, каждая точка M (x, y) которой отстоит от точки F(4,0) на расстоянии вдвое большем, чем до прямой x= 1.
3.4.Парабола
3.4.1.Каноническое уравнение гиперболы
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается p
( p 0 ).
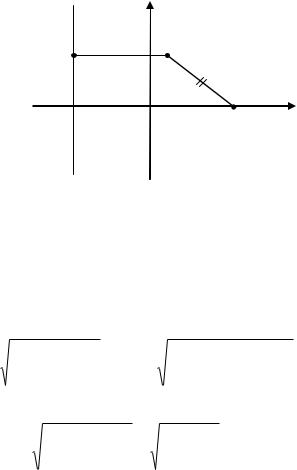
Для вывода уравнения параболы выберем систему координат так, чтобы ось OX проходила через фокус F перпендикулярно директрисе в направлении от директрисы к фокусу, а начало координат О расположим посередине между фокусом и директрисой (рис. 3.8). В выбранной
|
|
p |
|
|
системе координат фокус F имеет координаты |
|
,0 , а уравнение директрисы имеет вид |
||
|
||||
|
|
2 |
|
|
x |
p |
. |
|
|
|
|
|||
2 |
|
|
|
|
57
|
N |
|
|
|
Y |
|
M(x,y) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
p |
|
|
|
O |
|
F(p/2,0) |
X |
|
|
|
|
|
|
||||
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
2
Рис. 3.8. Геометрическое построение к выводу уравнения параболы
Пусть M (x, y) – произвольная точка парабола. Соединим точку M и F. Проведем отрезок
MF перпендикулярно директрисе. Согласно определению параболы |
MF MN , расстояние ме- |
||||||||||||
жду двумя точками находим по формулам |
|
|
|
|
|
|
|
|
|
|
|||
|
|
p 2 |
2 |
|
|
|
p 2 |
|
|
2 |
|
||
MF |
x |
|
y |
|
, |
MN |
x |
|
|
( y y) |
|
. |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||
Следовательно,
|
p 2 |
|
2 |
|
|
p 2 |
|
||||||
x |
|
|
|
y |
|
|
x |
|
. |
|
|||
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
2 |
|
||||||
Возведя обе части в квадрат получим |
|
|
|
|
|
|
|
|
|
||||
x2 px |
p |
2 |
y2 x2 px |
p |
2 |
, |
|||||||
|
|
||||||||||||
|
4 |
|
|
|
|
|
4 |
|
|
||||
То есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 2 px. |
|
|
|
|
(3.10) |
|||
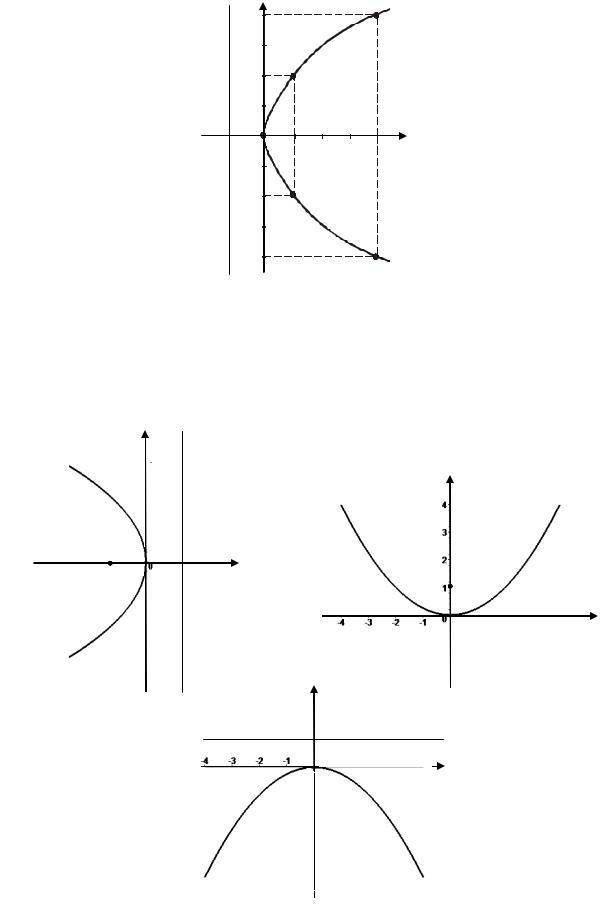
Уравнение (3.10) – каноническое уравнение параболы (рис. 3.9).
3.4.2.Исследование формы параболы
1.В уравнение (3.10) переменная входит в четной степени, значит, параболы симметрично относительно оси ОХ; ось ОХ является осью симметрии параболы.
2.Так как p 0 , то из уравнения (3.10) следует, что x 0 . Следовательно, параболы расположена справа от оси OY.
3.Очевидно, что парабола проходит через начало координат. Точка O называется верши-
ной параболы, отрезок FM = r называется фокальным радиусом точки M.
4.При неограниченном возрастании x модуль y также неограниченно возрастает.
58
|
Y 4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
F(p/2,0) |
|
|
||
|
00 |
1 |
2 |
3 |
4 |
X |
|
-1 |
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
-3 |
|
|
|
|
|
x p / 2 |
-4 |
|
|
|
|
|
Рис. 3.9. |
Парабола |
y2 2 px |
||||
3.3.3. Различные виды параболы |
||||||
Уравнения вида y2 2 px , x2 2 py , x2 2 py ( p 0 ) также определяют параболы, они изображены на рис. 3.10.
Y
Y
|
|
|
|
|
|
|
|
|
F(- |
p/2,0) |
0 |
X |
|
|
F(0,p/2) |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
x p / 2 |
|
|
X |
|
|
|
|
|
|
|
|
|
y p / 2 |
|
Y
y p / 2

 0
0
X
 F(0,-p/2)
F(0,-p/2)
Рис. 3.10. Виды различной ориентации параболы
59
Задачи и упражнения для самостоятельной работы
3.11. Составить уравнение параболы, построить ее, если:
а) парабола симметрична относительно оси ОХ, вершина лежит в начале координат и расстояние от фокуса до вершины равно 4;
б) парабола симметрична относительно оси ОХ, вершина лежит в начале координат и проходит через точку (2,-4);
в) парабола симметрична относительно оси ОХ, вершина лежит в начале координат и проходит через точку (-2,4);
г) парабола симметрична относительно оси ОY, вершина лежит в начале координат и фокус лежит в точке (0,3);
д) парабола симметрична относительно оси ОY, вершина лежит в начале координат и проходит через точку (4,2);
е) парабола симметрична относительно оси ОY, вершина лежит в начале координат и проходит через точку (-4, -2).
3.12. Составить уравнение линии, каждая точка M (x, y) которой одинаково удалена от начала координат и от прямой x= -4.
3.5. Кривые второго порядка с осями симметрии, параллельными координатным осям
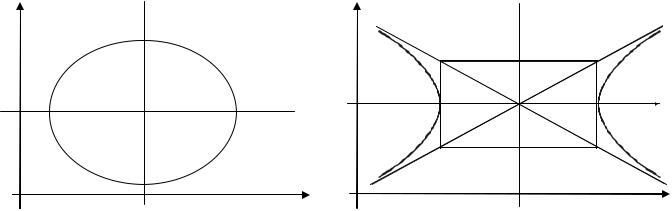
Уравнение эллипса с центром в точке O1(x0 , y0 ) , оси симметрии которого параллельны координатным осям OX и OY, а полуоси соответственно равны а и b, имеет вид (рис. 3.11 а)
|
(x x )2 |
|
( y y )2 |
1. |
|
|
0 |
0 |
(3.11) |
||||
|
а2 |
b2 |
||||
|
|
|
|
|
||
Уравнение гиперболы с центром в точке O1(x0 , y0 ) , оси симметрии которой параллельны |
||||||
координатным осям OX и OY, а полуоси соответственно равны а и b, |
имеет вид (рис. 3.11 б) |
|||||
|
(x x )2 |
|
|
( y y )2 |
1. |
|
0 |
|
0 |
(3.12) |
|||
|
а2 |
|
b2 |
|||
|
|
|
|
|
||
Y Y
y
b
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
y0 |
|
|
-a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||
y |
|
O1 |
а |
|
|
O1 |
а |
x |
||||
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-b |
|
|
|
|
O |
x0 |
|
O |
x0 |
|
|
|
X |
||||
|
|
|
|
X |
|
|
|
|
|
|||
|
|
а) Эллипс |
|
|
|
|
б) Гипербола |
|
|
|
|
|
|
|
|
Рис. 3.11. Кривые с центром симметрии в точке O1(x0 , y0 ) |
|
|
|
|
|||||
60
