
2979
.pdf
Единичная матрица - диагональная матрица, у которой все элементы главной диагонали aii=0, i 1, n.
|
1 |
0 |
0 |
0 |
0 |
||
|
|
0 |
1 |
0 |
0 |
0 |
|
I |
|
|
|||||
|
|
|
|
|
|
. |
|
|
|
|
|
||||
|
|
|
|||||
|
|
|
|
|
|
||
|
|
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|||||
0, при i j aij ij 1, при i j.
Здесь ij - символ Кронекера, i, j 1, n .
Симметрическая матрица - матрица, у которой все элементы aij=aji, i, j 1, n. В этом случае говорят, что элементы матрицы симметричны относительно главной диагонали. Если aij=- aji, i, j 1, n , то матрица называется кососимметрической.
Нулевая матрица - матрица, у которой все элементы aij=0,
i 1, m, j 1, n.
|
0 |
0 |
|
0 |
||
|
|
0 |
0 |
|
0 |
|
|
|
|
||||
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|
||
|
|
0 |
0 |
0 |
0 |
|
|
|
|
||||
Матрица называется ступенчатой, если она имеет вид:
|
a11 |
a12 |
a1,r 1 |
a1r |
a1n |
|
|
|
|
0 |
a22 |
a2,r 1 |
a2r |
a2n |
|
A |
|
|
|||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||
|
|
|
|||||
|
|
|
|
|
|
||
|
|
0 |
0 |
0 |
arr |
|
|
|
|
arn |
|||||
|
|
|
|
21 |
|
|
|

где aii 0 , для всех r n .
Матрица, состоящая из одной строки, называется векторомстрокой, матрица, состоящая из одного столбца - вектором-
столбцом.
Две матрицы A и B называются равными (A=B), если они имеют одинаковые размеры и их соответствующие элементы равны.
Матрица B 
 bij
bij 
 называется транспонированной к матрице
называется транспонированной к матрице
A 
 aij
aij 
 , если bij=aji i 1, m, j 1, n. Обозначение: B=AТ.
, если bij=aji i 1, m, j 1, n. Обозначение: B=AТ.
|
a |
a |
a |
|
|
a |
a |
a |
|
|
||
|
|
11 |
12 |
1n |
|
|
11 |
21 |
|
m1 |
|
|
A |
a |
a |
a |
|
; AТ |
a |
a |
a |
|
|
||
|
21 |
22 |
2n |
|
12 |
22 |
m2 |
. |
||||
m n |
|
|
|
|
|
m n |
|
|
|
|
|
|
|
|
|
a |
a |
|
|
|
|
a |
a |
|
|
|
a |
|
|
a |
mn |
|
||||||
|
|
m1 m2 |
mn |
|
|
1n 2n |
|
|
||||
|
|
|
3 |
2 |
4 |
|
|
|
|
|
3 |
1 |
|
|
A2 3 |
; |
T |
|
|
2 |
7 |
|
|||||
Пример. |
|
1 |
7 |
9 |
|
A3 2 |
|
. |
|||||
|
|
|
|
|
|
|
|
4 |
9 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2.Определитель n-го порядка
2.1.Определение. Вычисление определителей 2-го и 3-го
порядков
Определение. Перестановкой J n-го порядка называется всякое расположение n чисел 1, 2, , n.
Общее число всех перестановок n-го порядка равно
def
n! 1 2 n (читается эн-факториал).
В общем виде перестановку записывают в виде векторстроки: J=(j1 j2 jn). Перестановка (1 2 n) называется нор-
мальной.
22

Беспорядком или инверсией в перестановке J называется наличие пары чисел, в которой большее число предшествует меньшему.
Число инверсий в перестановке J обозначим r(J). Если это чётное, то перестановка называется чётной, иначе – нечёт-
ной.
Определение 1. Определителем (детерминантом) n-го по-
рядка квадратной матрицы A называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по одному из
каждой строки и каждого столбца, причём знак каждого члена определяется как (-1)r(J), где r(J) – число инверсий в пере-
становке J из номеров столбцов элементов матрицы (j1 j2 jn), если при этом номера строк записаны в порядке возрастания:
|
a11 |
a12 |
a1n |
|
|
|
|
det A |
a21 |
a22 |
a2n |
r J |
a1j |
a2 j |
anj , |
|
|
|
1 |
||||
|
|
1 |
2 |
n |
|||
|
|
|
|
|
an1 an2 ann
где сумма берётся по всем перестановкам J.
Определители второго и третьего порядков.
Пусть n=2. Существует 2!=1 2=2 перестановки номеров столбцов матрицы
a11
A
a21
a12 .
a
22
Составим перестановки номеров столбцов
J1=(1 2) r(J1)=0 J2=(2 1) r(J2)=1 (1 2)
Тогда, по определению 1,
23

det A |
a11 |
a12 |
1 0 a a |
22 |
1 1 a |
a |
21 |
|
a21 |
a22 |
11 |
12 |
|
||
|
|
|
|
|
|
a11a22 a12a21.
Мнемоническое правило: определитель второго порядка равен разности произведения элементов главной диагонали и произведения элементов побочной диагонали.
Пример. 2 3 2 5 3 4 10 12 2. 4 5
Пусть n=3. Существует 3!=123=6 перестановок номеров столбцов.
|
|
|
a11 |
a12 |
a13 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
A a21 |
a22 |
a23 |
|
|
|||
|
|
|
|
|
a32 |
a33 |
|
|
|
|
|
|
a31 |
|
|
||||
J1=(1 2 3) |
r(J1)=0 |
J3=(2 1 3) |
r(J3)=1 |
J5=(3 1 2) |
r(J5)=2 |
||||
|
|
|
|
(1 2 3) |
|
|
(1 3 2) |
|
|
|
|
|
|
|
|
|
|
(1 2 3) |
|
J2=(1 3 2) |
r(J2)=1 |
J4=(2 3 1) |
r(J4)=1 |
J6=(3 2 1) |
r(J6)=3 |
||||
(1 2 3) |
|
|
|
(2 1 3) |
|
|
(2 3 1) |
|
|
|
|
|
|
(1 2 3) |
|
|
(2 1 3) |
|
|
|
|
|
|
|
|
|
|
(1 2 3) |
|
Тогда, по определению 1 име- |
|
|
|
|
|
||||
|
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ем det A |
a21 |
a22 |
a23 |
|
|
|
|
||
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
24

1 0 a11a22a33 1 1 a11a23a32 1 1 a12a21a331 2 a12a23a31 1 2 a13a21a32 1 3 a13a22a31 a11a22a33 a11a23a32 a12a21a33 a12a23a31 a13a21a32 a13a22a31
a11a22a33 a12a23a31 a21a32a13
a13a22a31 a12a21a33 a23a32a11.
Правило Сарруса.
Определитель третьего порядка равен алгебраической сумме шести тройных произведений элементов, взятых по одному из каждой строки и каждого столбца соответствующей матрицы; со знаком + берутся произведения, сомножители которых находятся на главной диагонали и в вершинах тре-
угольников с основаниями, параллельными главной диагона-
ли; со знаком - берутся произведения, сомножители которых стоят на побочной диагонали и в вершинах треугольни-
ков с основаниями, параллельными этой диагонали (см. рис.
6.).
Рис. 6. Произведения элементов матрицы со знаком «+» и «-»
25
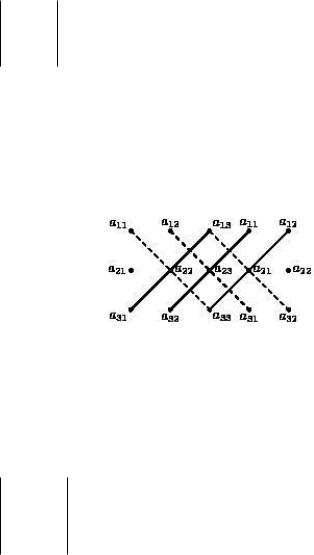
Пример. 1 0 3
2 4 6 1 4 8 0 6 5 2 7 3 3 4 5 0 2 8 6 7 1 28. 5 7 8
Существует также другое мнемоническое правило Сарруса вычисления определителя третьего порядка: приписать к определителю справа два первых столбца, не меняя их, и составить сумму произведений элементов главной диагонали и элементов, параллельных ей, из которой затем вычесть сумму произведений элементов побочной диагонали и элементов, параллельных ей:
Рис.7. Другое правило Сарруса
На рисунке 7 пунктиром показаны произведения со знаком плюс, а сплошной линией – со знаком минус:
det A a11a22a33 a12a23a31 a13a21a32
a13a22a31 a12a21a33 a23a32a11.
Для предыдущего примера:
1 0 3 1 0 2 4 6 2 4 1 4 8 0 6 5 3 2 7 3 4 5 1 6 7 5 7 8 5 7
0 2 8 32 0 42 60 42 0 28.
26

2.2. Миноры и алгебраические дополнения
Минором Mij элемента aij квадратной матрицы n-го порядка
A называется детерминант матрицы (n-1)-го порядка, полученной из матрицы A вычёркиванием i-ой строки и j-ого столбца, на пересечении которых расположен элемент aij.
Алгебраическим дополнением (адъюнктом) Aij элемента aij
квадратной матрицы A n-го порядка называется его минор, взятый со знаком (-1)i+j: Aij=(-1)i+jMij.
Теорема Лапласа (о разложении определителя). Определи-
тель квадратной матрицы равен сумме произведений всех элементов любой строки (столбца) на их алгебраические дополнения:
n
ai1Ai1 ai2Ai2 ainAin aijAij j 1
(разложение по элементам i-ой строки, i 1, n )
n
или a1jA1j a2 jA2 j anjAnj aijAij i 1
(разложение по элементам j-ого столбца, j 1, n. )
Следствие 1. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения элементов другой строки (столбца) этой матрицы равны 0, т.е.
n
aisAis 0 при i j. s 1
Следствие 2. Сумма произведений произвольных чисел b1, b2, , bn на алгебраические дополнения элементов любой строки (столбца) равна детерминанту матрицы, полученной из данной заменой элементов этой строки (столбца) на числа b1, b2, , bn.
Практически определитель раскладывают по элементам строки или столбца, в которых больше всего нулей.
27

|
|
1 |
1 |
2 |
|
|
1 |
|
|||
Пример. Вычислить |
0 |
1 |
2 |
1 |
. |
|
1 |
1 |
0 |
1 |
|
|
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
Решение.
Первый способ. Разложим по элементам четвёртой строки. Вычислим алгебраические дополнения её ненулевых элементов.
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|||
A 1 4 2 M |
42 |
1 4 2 |
0 |
1 2 |
1 |
|
|||||
42 |
|
|
|
|
1 |
1 |
0 |
1 |
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
0 |
2 |
1 |
2 0 1 4 0 0 3. |
|
|
|||||
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
1 |
1 |
1 |
|
|
1 |
|
|
||||||
|
|
|
|||||||
|
0 1 2 |
1 |
|
|
|||||
A 1 4 4 |
|
0 1 |
2 |
|
|||||
44 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
1 |
1 |
0 |
|
||||
|
0 |
1 |
0 |
1 |
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 2 0 1 0 2 1.
Тогда по теореме Лапласа =a42A42+a44A44=1 (-3)+1 1=-3+1=- 2.
Второй способ. Разложим по элементам третьего столбца. Для этого вычислим алгебраические дополнения его ненулевых элементов.
28
|
|
|
|
|
0 |
1 |
1 |
|
|
A 1 1 3 |
M 1 4 |
1 1 1 |
|
||||||
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
0 0 1 0 1 0 0. |
|
|
|
|
|
||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
||
A 1 2 3 |
M |
23 |
|
1 1 |
1 |
|
|||
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 0 2 0 1 1 1.
Таким образом, =a13A13+a23A23=(-1)0+2 (-1)=-2.
Третий способ. Разложим по элементам первого столбца. Для этого вычислим алгебраические дополнения его ненулевых элементов.
|
|
|
|
1 |
2 |
1 |
|
|
|
A 1 1 1 M |
|
|
1 0 1 |
0 2 0 0 2 0 0. |
|||||
11 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
|||
A 1 3 1 M |
31 |
|
1 |
2 |
|
1 |
|
||
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 1 0 4 1 0 2.
a11 A11 a31 A31 1 0 1 ( 2) 2 .
2.3.Свойства определителя n-го порядка
1.Если какая-либо строка (столбец) матрицы A состоит из одних нулей, то detA=0.
2.При перестановке двух строк (столбцов) матрицы её определитель меняет знак на противоположный.
29

3.Если матрица A содержит две одинаковые строки (столб-
ца), то detA=0.
4.Общий множитель любой строки (столбца) можно выносить за знак определителя.
5.Если элементы двух строк (столбцов) матрицы A пропорциональны, то detA=0.
6.Линейность детерминанта. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей, в каждом из которых:
а) все строки (столбцы), за исключением указанной строки (столбца), совпадают с аналогичными стро-
ками (столбцами) определителя ; б) на месте указанной строки (столбца) первый опре-
делитель содержит первые слагаемые, а второй – вторые слагаемые данной строки (столбца) определителя .
Пусть i и j меняются от 1 до n. Тогда
|
a11 |
a12 |
a1 j |
a1n |
|
||||
|
a21 |
a22 |
a2 j |
a2n |
|
||||
|
a' |
a" |
a' |
a" |
a' |
a" |
a' |
a" |
|
|
i1 |
i1 |
i2 |
i2 |
ij |
ij |
in |
in |
|
|
an1 |
an2 |
anj |
ann |
|
||||
30
