2979

ГЛАВА 5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

1. Постановка задачи линейного программирования (ЗЛП)

Линейное программирование - наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений. Математическое выражение целевой функции и её ограничений называется математической моделью задачи.

В общем виде ЗЛП ставится следующим образом (общая ЗЛП): найти максимум (минимум) функции

где x j ( j 1, n ) - управляющие переменные или решения зада-

чи (1)-(2), аij, bi, сj, i=1, m , j=1, n , - заданные числа (парамет-

ры), F-целевая функция или критерий эффективности (оп-

тимальности) задачи. Функция (1) - линейная, ограничения

(2) - линейные. Задача содержит n переменных и m ограниче-

121

ний. Решить ЗЛП - это значит найти значения управляющих

переменных xj, j=1, n , удовлетворяющих ограничения (2), при

которых целевая функция (1) принимает экстремальное значение.

Основной (канонической) ЗЛП называется задача, состоящая в определении максимума целевой функции при ограничениях, заданных равенствами и x j 0 .

Допустимым решением (планом) ЗЛП называется вектор

X=(x1, x2, …, xn), удовлетворяющий системе ограничений (2). Множество допустимых решений образует область допу-

стимых решений (ОДР).

Допустимое решение Х*= x1* , x2* ,..., xn* , при котором целевая

функция достигает своего экстремального значения, называ-

ется оптимальным решением ЗЛП.

2. Графический метод решения ЗЛП

Если число переменных в ЗЛП равно 2, а ограничениями является система неравенств, то задачу можно решать графическим методом. Он применим для решения ЗЛП следующего вида:

Алгоритм решения ЗЛП графическим методом.

1.Записывают уравнения прямых, соответствующих ограничениям (4) и строят их на плоскости X1OX2.

2.Определяют области, в которых выполняются ограничения задачи. Для этого выбирают произвольную точку на

плоскости X1OX2 и подставляют ее координаты в левую часть одного из неравенств. Если неравенство верно, то искомая полуплоскость находится с той же стороны от прямой, что и

122

точка; иначе искомая полуплоскость находится с противоположной стороны от прямой.

3.Эти действия выполняются последовательно для всех неравенств (4).

4.Определяют ОДР задачи (многоугольник решений) как область пересечения m полуплоскостей, соответствующих m ограничениям задачи.

5.Определяют направление возрастания (убывания) целевой функции F. Для этого строят вектор-нормаль n гради-

направление показывает направление возрастания функции F,

впротивоположном направлении функция убывает.

6.Определяют граничную точку (точки) ОДР, в которых целевая функция принимает максимальное или минимальное значение.

7.Для этого строят линию уровня F0 c1x1 c2 x2 0 це-

левой функции и передвигают ее в направлении вектора n =(c1;c2) до тех пор, пока она не пройдет через последнюю её общую точку с многоугольником решений.

8. Вычисляют значения координат найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка, или, выявляя уравнение граничной прямой ОДР, с которой совпадает линия уровня целевой функции. Возможны следующие варианты ОДР: замкнутое множество, открытое множество, пустое множество (система ограничений несовместна), единственная точка. Пересечение линии уровня целевой функции может состоять из одной точки или целого отрезка. Максимальным (минимальным) значением целевой функции может быть как конечное число, так и бесконечность.

Пример. Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются 2

123

исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы приведены в таблице.

Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более, чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 д. е., шоколадно- го-14 д. е.

Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?

Решение. Обозначим: x 1 – суточный объем выпуска сливочного мороженого, кг; x 2 – суточный объем выпуска

шоколадного мороженого, кг. Составим математическую модель задачи.

Целевая функция будет иметь вид:

F=16x 1 +14x 2 max. (5)

Система ограничений:

Построим в плоскости X1OX2 область допустимых решений, то есть решение системы ограничений (6) (см. рис.20). Для этого, заметим, что каждое неравенство системы ограни-

124

чений определяет в плоскости X1OX2 полуплоскость, лежащую выше или ниже прямой, определяемой соответствующим уравнением.

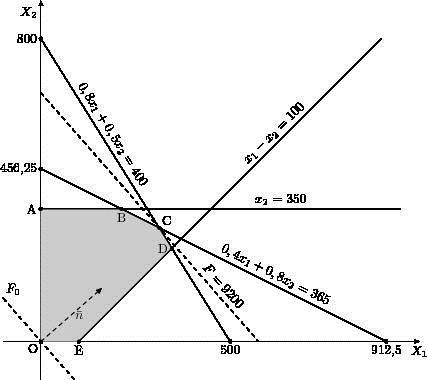
Построим прямые: 0,8x 1 +0,5x 2 =400, 0,4x 1 +0,8x 2 =365, x 1 -x 2 =100, x 2 =350, x 1 =0, x 2 =0. Точки пересечения этих прямых обозначим A, B, C, D, E.

Рис.20. Решение задачи линейного программирования

Рассмотрим первое неравенство системы ограничений (6). Чтобы построить его решение, возьмём, например, точку с координатами x 1 =0, x 2 =0. Подставив их в неравенство, получаем 0 400 – верно, следовательно, искомая полуплоскость (решение) лежит ниже прямой 0,8x 1 +0,5x 2 =400, остальные

125

полуплоскости находятся аналогичным образом. В результате пересечения всех этих областей получаем область OABCDE - ОДР задачи. Для нахождения максимального значения целевой функции F проверим граничные точки из области реше-

нормали n =(16;14) градиента целевой функции параллельно самой себе, пока хотя бы одна её точка будет принадлежать ОДР. По рисунку видно, что точкой выхода из ОДР является точка С. Её координаты определяются из системы:

0,8x1 0,5x2 4000,4x1 0,8x2 365.

Решая её, найдем координаты точки С: x 1 =312,5 и x 2 =300. В точке С и будет оптимальное решение X*=(312,5; 300). При этом F max =16∙312,5+14∙300=9200(д. е.). Таким образом, фирма

должна выпускать в сутки 312,5 кг сливочного мороженого и 300 кг шоколадного мороженого, при этом доход от реализации составит 9200 д.е.

3. Симплекс – метод решения ЗЛП

Симплекс (лат. simplex) – простейший выпуклый многогранник в n- мерном пространстве с n+1 вершиной (например, тетраэдр в трёхмерном пространстве); симплексом явля-

смысл симплекс-метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере не худшее) значение (по отношению к цели задачи), до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение целевой функции (если задача имеет

126

конечный оптимум). Впервые симплекс-метод был предложен американским учёным Дж. Данцигом в 1949 г., однако, ещё в 1939 г. идеи метода были разработаны российским математиком Л.В.Канторовичем.

Для применения симплекс-метода общую ЗЛП следует записать в основной (канонической) форме:

Правила перехода к канонической форме.

1.Если требуется найти min F, то заменяя F на (-F), переходят к задаче максимизации, т.е. min F = max (-F).

2.Если ограничение является неравенством со знаком ≤, то от него переходят к равенству, прибавляя к левой части ограничения дополнительную неотрицательную переменную.

3.Если ограничение является неравенством со знаком ≥, то от него переходят к равенству, вычитая из левой части дополнительную неотрицательную переменную.

4.Если в задаче какая – либо из переменных произвольная, т.е. не подчиняется условию неотрицательности, то от неё избавляются, заменяя её разностью двух других неотрицательных переменных. Например, для произвольной пере-

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений – неравенств в ограничения–равенства равно числу преобразуемых неравенств. Вводимые дополнительные переменные имеют вполне определённый смысл. Так, если в ограничениях исходной ЗЛП отражаются расход и наличие производственных

127

ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объёму неиспользованного соответствующего ресурса.

Задача (7) – (9) не всегда имеет решение. Во-первых, система уравнений (8) может оказаться несовместной. Вовторых, она может оказаться совместной не в области неотрицательных решений. В-третьих, допустимые решения системы (8)-(9) существуют, но среди них нет оптимального: функция (F) не ограничена в ОДР. Предположим, что все уравнения системы (8) линейно независимы, т.е. выражают независимые друг от друга условия задачи. Если это не так, то лишние уравнения нужно исключить. Задачу (7)-(9) имеет смысл решать, когда число уравнений в системе (8) ограничений меньше числа входящих в них неизвестных: m<n. Иначе, если m=n, то система (8) имеет единственное решение и задача максимизации функции (7) не имеет смысла; если m>n, то система (8) переопределена и в общем случае не имеет решений. Если m<n, то система (8) имеет бесконечное множество решений и среди них можно выбрать оптимальное, в котором целевая функция достигает своего максимума.

Симплекс–метод является методом направленного перебора решений системы (8)-(9). Каждое следующее решение улучшает значение целевой функции.

Симплекс – метод включает 2 этапа:

1)определение начального решения, удовлетворяющего ограничениям (8)-(9);

2)последовательное улучшение начального решения и получение оптимального решения задачи(8) - (9) .

Система (8) содержит m линейно независимых уравнений и их число меньше числа неизвестных, входящих в систему, следовательно, систему (8) можно разрешить относительно m неизвестных, например, x1, x2,…, xm, выразив их через остальные неизвестные:

128

дый из векторов Рj, j 0, n, можно разложить по этому базису:

ется оптимальным планом, если ∆j≥0, j 1, n .

Теорема 2. Если j<0 для некоторого j=k и среди чисел aik, i 1, m , нет положительных (aik0, i 1, m ), то целевая функция (11) задачи (11)-(13) не ограничена на множестве её планов.

Теорема 3. Если опорный план задачи (5) - (7) не вырожден и ∆k < 0, но среди чисел aik, i 1, m , еcть m положительных

(не все aik≤0, i 1, m ), то существует опорный план X , та-

кой, что F( X )>F(X).

В столбце cб записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса. В столбце Р0 записывают положительные компоненты исходного опорного плана, в нём же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов Рj представляют собой столбцы коэффициентов разложения этих векторов по векторам данного базиса.

130