Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2979

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.72 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2012 13 14 15 16 17 18 19 20 > Следующая >>>

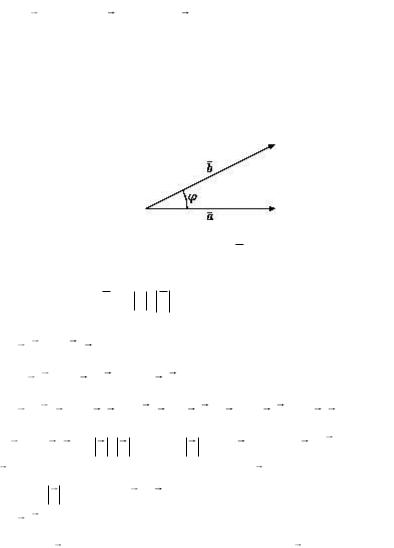
Углы между вектором и осями координат.

cos

; cos

- направляющие косинусы

вектора a .

cos2 cos2

cos2

a2y

ax2 a2y az2

Скалярное произведение векторов.

Рис. 17. Скалярное произведение

Для векторов a ax , ay , az , b bx ,by ,bz определим скалярное произведение (число) по формуле (см. рис. 17.)

a,b a b cos axbx ayby azbz .

Свойства скалярного произведения.

1.a,b b, a ;

2.a, b a,b a,b ;

3.a b, c a, c b, c ; a,b c a,b a,c ;

4. a2 a, a a a cos0 a 2 0; a2 0 a 0. a 2 называется скалярным квадратом a .

5.Если e 1, то e, e .

6.a, b 0 тогда и только тогда, когда вектор a перпенди-

кулярен b или один из этих векторов равен 0 .

111

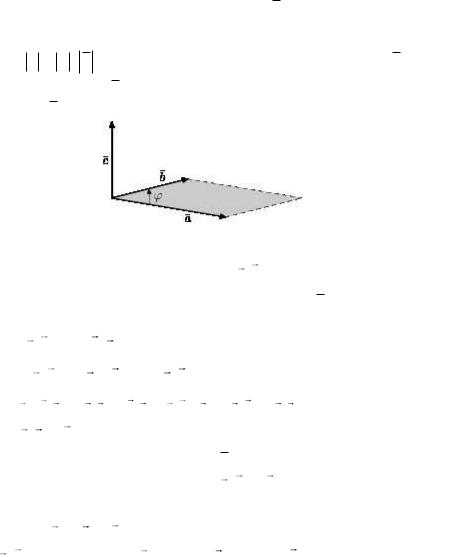
Векторное произведение двух векторов.

Векторное произведение векторов a и b (см. рис.18.) – это


вектор	a,	b	c такой, что

1. c a b sin , где – угол между векторами a и b ;

2.c a и c b ;

3.a , b , c образуют правую тройку.

Рис.18. Векторное произведение

Геометрический смысл векторного произведения.

Модуль векторного произведения a, b равен площади S па-

раллелограмма, построенного на векторах a и b .

Свойства векторного произведения.

1.a,b b, a (антикоммутативность).

2.a,b a,b a,b .

3.a b, c a, c b, c ; a, b c a, b a, c .

4.a, a 0.

5.Для того, чтобы векторы a и b были коллинеарны, необ-

ходимо и достаточно, чтобы a, b 0.

Координаты векторного произведения.

a, b

a a

112


a, b			ay
a, b			b
			b
			y
			y

ay	az	j	az	ax	k	ax	ay		.
b	b		b	b		b	b	y
y	z		z	x		x		y

a ax ;ay ;az

;

b bx ;by ;bz .

Смешанное произведение трёх векторов.

a, b , c abc (a,b , c ).

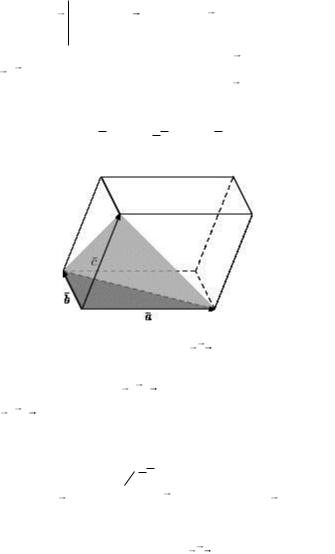
Геометрический смысл смешанного произведения.

Рис.19. Смешанное произведение

Смешанное произведение abc трёх некомпланарных векторов равно объёму параллелепипеда (см. рис.19.), по-

строенного на векторах a,b, c , взятому со знаком + , если

тройка a,b, c – правая, со знаком - , если эта тройка – левая. Объём пирамиды, построенной на этих же векторах (см. серая область на рис.19.) в 6 раз меньше объёма указанного параллелепипеда и равен 16 abc .

Теорема. Если a ax ;ay ;az , b bx ;by ;bz ,		c cx ;cy ;cz ,
	ax	ay	az
	ax	ay	az
то смешанное произведение равно abc	bx	by	bz
	cx	cy	cz
113

x y ( x1 y1, x2 y2 , x3 y3 ) ,

Свойства смешанного произведения.

1.Для того, чтобы векторы a , b и c были компланарны, необходимо и достаточно, чтобы a, b, c 0.

2.a,b , c a, b, c .

3.Смешанное произведение не меняется при круговой (циклической) перестановке сомножителей. Перестановка двух соседних сомножителей меняет знак произведения.

abc bca cab bac cba acb.

Двойное векторное произведение.

Двойное векторное произведение трёх некомпланарных векторов определяется так: a, b, c . Этот вектор компланарен

векторам b и c .

Теорема. Двойное векторное произведение можно вычислить по правилу: a, b, c a, c b a,b c для любых векторов

a , b и c .

Определение евклидова векторного пространства Rn.

Множество всех упорядоченных систем x (x1, x2 , , xn ) n действительных чисел, для которых определены линейные комбинации

где , R и		y ( y1, y2 ,	, yn ) и	скалярное	произведение
	n
	xi yi
x, y	xi yi	называется	n-мерным евклидовым векторным
	i 1
пространством Rn. Его элементы				x (x , x ,	, x ) называют-
				1 2	n

ся n-мерными векторами, а числа				x1 , i 1, n,	- их координа-
тами.
			114

Длина	x	вектора x			определяется равенством:

				def		n
				def		n
			x		x , x	xi2 .
						i 1

Разложение вектора по базису.

Определение. Система n-мерных векторов a1, a2 ,

вается линейно зависимой, если i R, i 1, m, i

i 1

m
i ai		0.

i 1

, an назы-

0 :

(1)

Если равенство (1) выполняется только тогда, когда

	то система векторов a1, a2 , , an называется ли-
i 0 i 1, m,
нейно независимой.
			m
Вектор	b	i ai			называется линейной комбинацией
			i 1

векторов ai , i	1, m.			Числа	i , i 1, m, называются коэффици-
ентами линейной комбинации.
Базисом данной системы векторов называется её под-

система, векторы которой линейно независимы, а любой другой вектор системы является их линейной комбинацией.

Ранг системы векторов – максимальное число линейно независимых векторов этой системы, т.е. число векторов в базисе.

Диагональной системой векторов называется следую-

щая система:

115

, a

, , a

r 1,1

, a

, , a

0, a22

, a32 , , ar

1,2 , ar 2 , , an 2

0, 0, a33 , , ar 1,3 , ar 3 , , an3

, где aii 0, i 1, r.

0, 0, 0, ,0, a

, , a

Теорема. Диагональная система векторов линейно независима.

Для вычисления ранга системы векторов нужно составить матрицу из этих векторов и привести её к ступенчатому виду. Число оставшихся в ней линейно независимых строк и есть ранг системы векторов.


Теорема. Если	a1 , a2			, , an - базис n-мерного пространства,

то произвольный вектор							этого пространства можно разло-
то произвольный вектор						b	этого пространства можно разло-
жить единственным					образом по векторам базиса, т.е.
		n

i R, i 1, n, : b			i		ai .

i 1

Практически разложение вектора по базису осуществляют двумя способами:

1. решают систему линейных уравнений

				и находят коэффициенты
1 a1	2 a2	n an b		и находят коэффициенты

i , i 1, n;

2.составляют расширенную матрицу из координат векторов и, выполняя прямой ход метода Гаусса, приводят её к трапециидальному виду.

			3, 6, 1 ,			3, 9, 3 образуют
Пример. Векторы	a1	1, 2, 1 , a2	3, 6, 1 ,		a3	3, 9, 3 образуют
базис в R3. Разложить по базису вектор					2, 5, 0 .
базис в R3. Разложить по базису вектор				b	2, 5, 0 .
		116

Решение. Первый способ:
Решение. Первый способ:																					1 a1				2 a2					3 a3							b.
															1							3					3					2

													1			2			2				6				3	9				5		.
																1							1					3				0

																1 3 2 3 3 2
																								9 3 5
																2 1 6 2								9 3 5

																1 2 3 3 0
1 3 3											1 3 3									9						1												9
1 3 3						9					1 3 3								2	9						1							3 3		2			9
																													2 3
	2 6 9					22						0 0 3							1	4							0		2 3						1					6
	1 1 3					3						0 4 6							2								0		1 1						1					4
	1 1 3					3						0 4 6							2	12							0		1 1						1					4

	2 0				3		1	0						2 0						3			1		0				6 0 0									6				12

		0 2 3					1	6							0 2 3								1		6					0 6 0								0				6
		0 0 6						8							0 0 3								1		4					0 0 3									1		4

							2 1 1
1 0 0					1		2 1 1
	0 1 0				0		1			2 1
	0 1 0				0		1			2 1
	0		0	3	1		4							1
	0		0	3	1		4			3
										3				3
														3
Искомое разложение:																									1												1
																b		a1			a2					a3 ;			b			1, 1,								.
																b		a1			a2				3	a3 ;			b			1, 1,					3			.
																									3												3
Второй способ.																										1			2 1 a1
1 2				1 a1						1 2 1 a1																1			2 1 a1


																			2
	3 6 1					a2					0 0 4							a	2		3a1						0		3 6				a3			3a1

	3 9 3					a3					0			3 6				a3			3a1						0		0 4				a2			3a1

	2 5 0										0 1 2																0		1 2
	2 5 0					b					0 1 2							b	2a								0		1 2				b				2a
																						1																		1
																						1																		1

	1 2 1				a1																1 2				1		a1


	0 3 6				a3		3a1														0 3				6		a3			3a1

	0 0 4				a2		3a1												=		0 0				4		a2			3a1							.

	0 0 0																				0 0				0
	0 0 0				3b		6a			a					3a						0 0				0		3b			3a		a
									1				3				1														1					3
									1				3				1														1					3

117

												1					1,0,	1	.
3b	3a	a	3	0	3b	3a	a	3	;	b	a		a	3	;	b
3b	3a	a		0	3b	3a	a		;	b	a		a		;	b
	1					1					1	3						3
												3						3

Если все векторы базиса попарно ортогональны, т.е.

			то такая система ненулевых векторов
		0 i j, i, j 1, n,
ai	, a j	0 i j, i, j 1, n,

называется ортогональным базисом евклидова пространства.

Если

j a j

и векторы

a j , j

1, n,

образуют орто-

j 1

гональный

базис,

то

a , ai j a j , ai 1 a1, ai 2 a2 , ai

j 1

i 1 ai 1, ai i ai , ai i 1 ai 1, ai

n an , ai

a , a

2 .

Откуда,

i i

a , ai ,

i 1, n.

(2)

Если в ортогональном базисе длины всех его векторов

равны 1, то такой базис называется ортонормированным.
Для ортонормированного базиса формула (2) примет вид:
i a, ai ,	i 1, n.	(3)

Наиболее важным примером ортонормированного базиса является базис, составленный из единичных векторов

e1 1, 0, 0,		, 0, 0 ,
e2	0, 1, 0,	, 0, 0 ,
en	0, 0, 0,	, 0, 1 .

Он называется единичным базисом. В пространстве R3 его об-

		1, 0, 0 ,			0, 1, 0 ,		0, 0, 1 .
разуют векторы	i	1, 0, 0 ,		j	0, 1, 0 ,	k	0, 0, 1 .
			118

Вопросы для повторения.

1.Вектор. Модуль вектора. Нулевой и единичный векторы. Коллинеарные, компланарные, равные, противоположные векторы,

2.Линейные операции над векторами и их свойства.

3.Геометрическая проекция вектора на ось (направление) и её свойства. Алгебраическая проекция.

4.Векторы в декартовой системе координат.

5.Скалярное произведение векторов и его свойства.

6.Векторное произведение векторов, его геометрический смысл и свойства. Координаты векторного произведения. Двойное векторное произведение.

7.Смешанное произведение векторов, его геометрический смысл и свойства.

8.Определение евклидова векторного пространства Rn.

9.Линейно зависимые и независимые системы векторов. Ранг системы векторов. Диагональная система векторов. Теорема о разложении вектора по базису. Ортогональный, ортонормированный, единичный базисы.

Задачи для самостоятельного решения.

1.	На векторах OA 5,10,15 и OB 0,10,5 построить
	треугольник OAB. Точка М делит сторону отрезка АВ в от-
	ношении 2:3. Найти координаты вектора OM .
2.	Построить треугольник с вершинами А(2,-3,1), В(4,11,6),
	С(4,-4,3). Найти длины сторон АС, АВ и угол ВАС.
3.	Построить	параллелограмм на векторах OA i j и
	OB 3i k .	Определить острый угол между диагоналями

	параллелограмма.
4.	Даны векторы a 3, 2,1 и	b 1,1, 2 . Найти вектор

	r , ортогональный a и b , если его длина равна 35.
	a 2,5,7 ; b 1,2,4 . Найти	a, b , (a,		) .
5.	a 2,5,7 ; b 1,2,4 . Найти	a, b , (a,	b	) .

	119

6.В пространстве даны 4 точки: А(1,1,1), В(4,4,4), С(3,5,5), D(2,4,7). Найти объём тетраэдра АВСD.

7.Показать, что векторы

x1 1,2,1,2 , x2 1,3,2,1 , x3 13, 1,2, 11

линейно зависимы. Найти эту зависимость.

8.Для системы векторов из задачи 1 найти все базисы.

9.Определить ранг системы векторов:

x1 1,2,3,4 , x2 2,3,4,1 , x3 3,4,1,2 , x4 4,1,2,3 . 10. Векторы a1 1,1,2 , a2 0,1, 1 , a3 3, 2,2 образуют

базис в R3. Разложить по этому базису вектор b 3,4,5 .

11. Найти векторы, дополняющие следующие системы до ортонормированных базисов:

a) 2 3 ; 13 ; 2 3 , 13 ; 2 3 ; 2 3 ;

б) 12 ; 12 ; 12 ; 12 , 12 ; 12 ; 12 ; 12 .

12. Даны

ортонормированные векторы a 1

; 1

,и

;0, 1

. Подобрать третий вектор c

так, чтобы

система a , b , c образовала ортонормированный базис.

13. Показать, что векторы a 1,2, 2,1 , b 1, 1, 1, 1 ор-

тогональны. Дополнить систему a , b до ортогонального базиса. Найти координаты вектора w 1,2,3,4 в этом базисе.

14.

Векторы a1

; 1

, a2 1

; 1

;0 ,

a3 1

; 1

, 2

образуют ортонормированный базис.

Найти в этом базисе координаты вектора a 4,3, 1 .

15.

Показать,

что

векторы

a 4,5,2 ,

3,0,1 , c 1,4,2

образуют базис в R3.

Разложить вектор d 5,7,8 по этому базису.

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2012 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.71 Mб22971.pdf
#
15.11.20222.72 Mб32972.pdf
#
15.11.20222.72 Mб12975.pdf
#
15.11.20222.72 Mб32976.pdf
#
15.11.20222.72 Mб42978.pdf
#
15.11.20222.72 Mб22979.pdf
#
15.11.20222.73 Mб22980.pdf
#
15.11.20222.73 Mб02981.pdf
#
15.11.20222.73 Mб02982.pdf
#
15.11.20222.74 Mб32983.pdf
#
15.11.20222.75 Mб52984.pdf