2979

Проверим выполнение достаточного условия сходимости метода итераций.

m max( 0,15;0,16;0,23) 0,23 1.

Подставив нулевое приближение в систему (4), получим первое приближение:

x1(1) 0, 78 0, 05* 0,82 0,1*1, 34 0, 955;

x2(1) 0,82 0,11* 0, 78 0, 05*1, 34 0, 9728;x3(1) 1, 34 0,11* 0, 78 0,12 * 0,82 1,5242.

101

Строим 2-ое приближение, подставив в систему (1) первое приближение и т.д., до тех пор, пока не достигнем требуемой точности.

max( 0,9863 0,9811 ; 1,0060 1,0013 ; 1,5681 1,5618 )

max(0,0052;0,0047;0,0063) 0,0063 .

x1(4) 0, 78 0, 05*1, 0060 0,1*1,5681 0, 9871;x2(4) 0,82 0,11* 0,9863 0, 05*1,5681 1, 0069;x3(4) 1, 34 0,11* 0, 9863 0,12 *1, 0060 1,5692.

Вопросы для повторения.

1.Система линейных уравнений. Матричная форма записи системы линейных уравнений.

2.Решения системы. Совместная, несовместная, определенная, неопределенная системы линейных уравнений.

3.Расширенная матрица системы линейных уравнений. Необходимое и достаточное условие совместности системы линейных уравнений (теорема Кронекера-Капелли).

4.Метод обратной матрицы. Метод Крамера. Формулы Крамера.

5.Метод Гаусса. Прямой и обратный ход. Недостатки метода Гаусса. Вычисление определителя с помощью метода Гаусса.

6.Алгоритм метода полного исключения. Вычисление обратной матрицы и ранга матрицы методом полного исключения.

7.Метод Гаусса с выбором главного элемента: схемы с выбором по строкам, по столбцам и по всей матрице.

8.Метод итераций решения систем линейных уравнений. Нулевое приближение. Условие сходимости итерационного процесса.

9.Условие диагонального преобладания. Коэффициент обусловленности системы.

10.Квадратичная форма. Матрица квадратичной формы. Матричная запись квадратичной формы. Ранг квадратичной формы.

11.Канонический вид квадратичной формы.

12.Собственные значения и собственные векторы матрицы. Характеристическое уравнение матрицы. Получение ортогональной матрицы. Геометрический смысл собственных значений и собственных векторов.

13.Ортогональное преобразование квадратичной формы.

103

14. Классификация квадратичных форм. Знакоопределённые квадратичные формы. Угловые миноры матрицы. Критерий Сильвестра.

Задачи для самостоятельного решения.

1. Методом обратной матрицы решить систему линейных уравнений:

2.Решить систему линейных уравнений в предыдущей задаче методом Крамера.

3.Методом Гаусса решить системы линейных уравнений:

4.Решить систему линейных уравнений в задаче 1 методами Гаусса и полного исключения.

5.Используя схемы с выбором главного элемента по строкам, столбцам и по всей матрице, решить систему линейных уравнений:

6. Решить систему линейных уравнений в задаче 1, используя схемы с выбором главного элемента по строкам, столбцам и по всей матрице.

104

8. Показать, что матрица A невырожденная. Найти обратную матрицу A-1, используя метод полного исключения, и проверить, что АА-1 = А-1A = I:

10. Найти ортогональное преобразование, приводящее к каноническому виду квадратичную форму

Q(x1 , x2 , x3 ) x12 2x1 x2 4x1 x3 5x22 4x32 ;

записать соответствующий канонический вид квадратичной формы.

11. Исследовать на знакоопределённость квадратичные формы:

a) Q(x1 , x2 , x3 ) x12 4x1 x2 2x1 x3 5x22 6x32 ; б) Q(x1 , x2 , x3 ) 3x12 x1 x2 2x2 x3 x22 3x32 .

12. При каких значениях k квадратичная форма Q(x1,x2,x3) является положительно определённой:

14)Q(x1 , x2 , x3 ) 3x12 kx22 4x1 x2 ;

15)Q(x1 , x2 , x3 ) x12 2x22 4x32 2kx1 x3 ?

105

ГЛАВА 4. ВЕКТОРНАЯ АЛГЕБРА

Вектор – направленный отрезок (см. рис. 9.). Будем обозна-

чать вектор с началом в точке A и концом в B так: AB , AB , a или a .

Единичный вектор – вектор a , такой, что a 1.

Коллинеарные векторы – векторы, лежащие на параллельных прямых (или на одной прямой).

Компланарные векторы – векторы, лежащие в параллельных плоскостях (или в одной плоскости).

Равные векторы a b - коллинеарные векторы, имеющие

одинаковые направления и равные длины.

Противоположные векторы a и ( a ) - векторы, противопо-

ложно направленные и имеющие одинаковые длины.

а) Правила треугольника и параллелограмма для двух векторов (см. рис. 10.).

Рис. 10. Сложение векторов

106

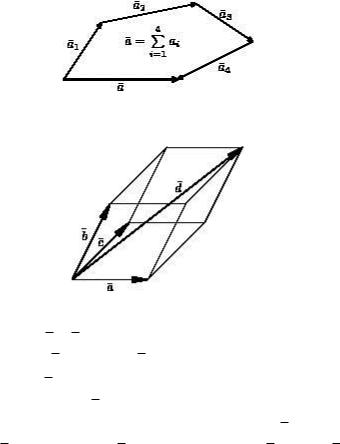
б) Правило многоугольника для нескольких векторов, лежащих в одной плоскости (см. рис.11.).

Рис.11. Правило многоугольника в) Правило параллелепипеда для трёх векторов, не лежа-

щих в одной плоскости (см. рис. 12.).

Рис. 12. Сложение трёх некомпланарных векторов

Свойства сложения векторов.

1.a b b a ;

2.(a b ) c a (b c ) ;

3.a 0 a ;

4.a (a ) 0 .

2.Вычитание векторов. Разность векторов a и b – это вектор a b c такой, что b c a , то есть a b a (b )

(см. рис.13.).

107

Рис.13. Вычитание векторов

3. Умножение вектора a на число .

Произведение вектора a на число это вектор b a такой, что

1)b a ;

2)0 a b ,0 a b.

b 0 , если a 0 или 0 .

Свойства умножения вектора на число.

1.( a ) ( )a ;

2.(a b ) a b ;

3.( )a a a .

Операция нахождения числа из векторного уравнения

b a называется делением вектора b на вектор a ( a и b

должны быть коллинеарными).

108

Проекция вектора AB на ось (направление) l. а) Геометрическая проекция - вектор A1B1 прl AB.

Рис.14. Геометрическая проекция

Свойства геометрической проекции.

1.прl (a b ) прla прlb ;

2.прl (a ) прl a .

б) Алгебраическая проекция – длина геометрической проекции.

Рис.15. Алгебраическая проекция прl AB AB cos , где – угол между AB и l .

Векторы в декартовой системе координат. Трёхмерный ортонормированный базис – система единичных векторов (ортов), расположенных на осях Ox, Oy, Oz и выхо-

дящих из начала координат: i , j , k , i j k 1.

109

к вектору j совершается против часовой стрелки. Если этот

поворот совершается по часовой стрелке, то такая тройка векторов называется левой.