Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2965

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

sin A2

2 sin

Так как b2

a1 , то

sin

a b

sin A1

и т.д.

1 sin B1 sin B2

Углы Ai ,

Bi и стороны ai,

bi (i = 1, 2, …, N), участвующие в передаче

длин сторон к следующему треугольнику, называют связующими, а Ci

и ci –

промежуточными.

Из последнего треугольника найдем

1 sin

sin

b .

1 sin B1 sin B2

sin BN

Сократив на b1 aN левую и правую части полученного выражения, полу-

чим

sin A1 sin A2

sin

(124)

sin B1 sin B2

sin BN

Выражение (124) приведем к линейному виду двумя способами.

1. Прологарифмировав (124), получим

lg sin Ai

lg sin Bi 0.

i 1

Заменив в этом выражении уравненные углы на измеренные с поправка-

ми, получим

(125)

lg sin Ai i

lg sin Bi i

i 1

Приращение функции lg sin Ai можно записать в виде

lg sin Ai lg sin Ai i A lg sin Ai .

Отсюда найдем

lg sin Ai i A lg sin Ai lg sin Ai .

Умножив и разделив последний член на поправку i A , запишем

A			lg sin Ai		A
lg sin Ai i	lg sin Ai				i	.
lg sin Ai i	lg sin Ai			A	i	.
				i
Обозначив
		lg sin Ai ,
	Ai	A
		i

получим

lg sin Ai		A	lg sin Ai A	A	.	(126)
lg sin Ai		i	lg sin Ai A	i	.	(126)
				i
Аналогичный вид имеет выражение для углов Bi.
В этих выражениях A	и	B	есть приращение (изменение) логарифма
i		i

синуса угла при увеличении самого угла Ai (Bi) на 1″ (если Ai и Bi берут до секунд).

Перепишем выражение (125) с учетом (126)

lg sin Ai

lg sin Bi

B i

i 1

Откуда получим полюсное условное уравнение в виде

(127)

A i

B i

WП

i 1

где WПlg lg sin Ai

lg sin Bi

– невязка (свободный член) полюсного условного

i 1

уравнения.

2. Полюсное условное уравнение в линейном виде удобно записать [10] как

WП 0,

(128)

qA i

qB i

i 1

где qAi

ctgAi

;

qBi ctgBi

;

WП

1 b1

(см);

П2

П1 sin A1 sin A2

... sin AN ;

П2 sin B1 sin B2 ... sin BN ;

3438

3400 .

Базисное условное уравнение.

1.Значение исходного базиса b2 (см. рис. 4, в) можно вычислить по теореме синусов на основе базиса b1 и уравненных углов треугольников:

sin A1

sin A2

sin AN

1 sin

sin B2

sin BN

или

sin

sin A2

sin

(129)

sin B1

sin B2

sin BN

Сравнивая выражения (129) и (124), можно видеть, что в выражении (129) присутствует дополнительный коэффициент b1 b2 . Поэтому условное уравнение базисов запишем по аналогии с выражением (124) как

– для полюсного условного уравнения

2,5m

Координатные условные уравнения. Условия координат (условия абс-

цисс и ординат) обычно возникают в несвободных геодезических сетях с исходными пунктами, непосредственно не связанными между собой. Вопрос составления координатных условных уравнений при уравнивании полигонометрических ходов рассмотрен ниже.

Определение допустимых величин свободных членов уравнений.

Под допустимыми величинами свободных членов условных уравнений понимают предельные погрешности тех функций, по которым вычисляются значения свободных членов.

После составления условных уравнений определяют допустимость свободных членов по формулам:

– для условных уравнений фигур и горизонта

n ;

Wдоп

N		A	N		B
A			B			lg	0,	(130)
		i			i	WБ
i 1	i		i 1	i

где

lg		N		N
WБ	lg b1	lg sin Ai	lg b2	lg sin Bi ,
		i 1		i 1

WБlg – невязка (свободный член) условного уравнения базисов в логарифмическом виде.

2.Базисное условное уравнение в линейном виде (по аналогии с выражением (128)

N		A	N			B
qA		A	qB			B	WБ 0,
qA		i	qB			i	WБ 0,
i 1	i		i 1		i
i 1			i 1
		W		П1		b b .
		W				b b .
		Б		П2		1	2
				П2

2,5m

;

2,5m

;

доп

П доп

i 1

– для базисного условного уравнения

mв1

mв2

Wдоп

2,5

2mlg b

;

WБдоп

;

i 1

в1

в2

– для условного уравнения дирекционных углов

Wдоп 2,52m2 n m2 .

В приведенных формулах приняты обозначения:

m – средняя квадратическая погрешность измерения угла; n – число уг-

лов в соответствующем уравнении; – приращение логарифма синуса угла при измерении угла на 1 ; mlg b – средняя квадратическая погрешность логарифма

базисной стороны; m – средняя квадратическая погрешность исходного дирекционного угла.

§24. Уравнивание полигонометрического хода коррелатным способом

Вполигонометрическом ходе А-В-1-2- … - С-D (рис.5), проложенном между двумя исходными пунктами В и С с известными координата-

ми хВ, уВ и хС, уС и двумя исходными сторонами с известными дирекционными углами αн и αк возникают геометрические условия дирекционных углов и координат. Этим условиям отвечают три условные уравнения поправок: уравнение дирекционных углов и два уравнения координат (абсцисс и ординат), т.е.

f1 н		i 180 n 1			к ;
		n 1
		i 1
		i 1

f2 d ,		n
f2 d ,	хВ di		cos i	хС ;		(131)
		i 1
f3 d ,		n
f3 d ,	уВ di		sin i	уC .
		i 1

Коэффициенты условных уравнений по-

правок, соответствующих выражениям (111),

найдем

как

частные

производные

функций

f1 , f2 , f3

по аргументам , d , .

Для первого уравнения (131) имеем

Рис.5. Схема к уравниванию

полигонометрического хода

(132)

т.е. a1 a2

an 1 1.

Для второго уравнения (131) имеем

bdi

d ,

cos i .

(133)

Для вычисления коэффициентов b i

2 d ,

запишем

1		н		1		180 ,
2		н		1		2		2 180 ,

.		. .		. .		. .		.	. .		,

	n		н		1		2			n	n 180 .

Из (134) найдем	i 1	, т.е.			i	i	и поэтому можно записать
	i				i	i
	i
		b i	f	2 d ,			b i .
		b i			i		b i .
					i

На основании выражения (131), учитывая (134) и (135), найдем

(134)

(135)

d ,

sin 1

sin 2

dn sin n

b 1

d ,

sin 2

dn sin n ,

b 2

. . . . . . . . . . . . . . .

. ,

d ,

sin n .

b n

n 1

Так как di sin i уi

, то из (136) получим

b у у

у ,

b 2 у2

уn у1 уC ,

. . . . . . . . . . . . .

b n уn уn 1 уC ,

b n 1

(136)

(137)

Аналогично найдем коэффициенты c i и c i условного уравнения орди-

нат:

cdi		sin i ,
c 1		хC хB ,
c 1		хC хB ,
c	2	х	х ,
	2	C	1			(138)
.		. .	. ,			(138)
.		. .	. ,
c	n	х	х	1	,
	n	C	n	1
c		0.
	n 1

С учетом выражений (132), (133), (137) и (138), запишем условные уравнения поправок для полигонометрического хода (см. рис. 5):

n 1
	1	W	0,
1	1
1

n			уB уC 1	у1 уC 2	уn 1 уC n	Wx
cos i di			уB уC 1	у1 уC 2	уn 1 уC n	Wx	0,	(139)
1
n			хC хB 1	хC х1 2	хC хn 1 n
sin i di			хC хB 1	хC х1 2	хC хn 1 n	Wy	0,
1

где невязки (свободные члены) определяются из выражений

W	n 1			180	n 1	,
		i	н			к
	1

Wx xi хC хB , 1

Wy уi уC уB . 1

Так как измеренные величины i , di неравноточные, то при уравнивании

необходимо учитывать их веса p	, p		или обратные веса q	1	p i	, q 1	,
i		di	i		p i	di	pdi
i		di	i			di

что более удобно в процессе решения нормальных уравнений. Обратные веса qi находят из выражения

qi mi2 ,

где mi – средняя квадратическая погрешность измерения; 0 – средняя квадра-

тическая погрешность единицы веса.

Выбор численного значения 0 зависит от точности создания сети. Учитывая, что горизонтальные углы i в полигонометрическом ходе обычно изме-

ряют с одинаковой точностью, запишем выражение для определения обратного веса углов в виде

	m2
q
			.
	2	2	.
	0

Так как длины линий хода имеют разную величину, то в этом случае мы имеем неравноточные измерения, и обратные веса измерений длин линий вычисляются по формуле

	md2		d	i
q	i	2			,

di	2			2
	0		0

где – коэффициент случайного влияния линейных измерений.

Если стороны измеряются электронными дальномерами, то обратные веса находят из выражения

	а b D	2
qdi	км	,
qdi	2	,
	0

где а и b – коэффициенты в уравнении для средней квадратической погрешности измерения длин линий дальномером; их значения выбирают в паспорте дальномера или в справочниках.

Условным уравнениям (139) соответствуют нормальные уравнения коррелат:

qaa k qab kx

qac ky

qab k qbb kx

qbc ky

(140)

qac k

qbc k

qcc k

Решив систему (140), найдем коррелаты и затем вычислим поправки в

измеренные углы i

и длины линий di

q k kx уB уC ky хC хB ;

q k kx у1 уC ky хC х1 ;

. . . . . . . . . . . .

. .

. ;

(141)

q k kx уn 1 уC ky хC хn 1 ;

qdi kx cos i ky

sin i

i 1, 2,

, n .

Приведенные выражения справедливы и для замкнутого полигонометрического хода, но в этом случае необходимо принять н к и хC хB , уC уB .

Глава 6. ПРЕДВАРИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ В СЕТЯХ

СГУЩЕНИЯ

§25. Содержание и порядок вычислений триангуляции

Целью предварительных вычислений является установление качества полевых измерений, соответствия их требованиям инструкций и необходимой точности, подготовка результатов измерений для уравнительных вычислений и оценка точности угловых измерений.

Предварительные вычисления начинаются в поле, во время производства наблюдений на пункте. Далее они продолжаются в камеральных условиях и включают в себя:

–проверку полевых материалов;

–составление сводов результатов измерений горизонтальных направлений на пунктах;

–составление схемы сети с измеренными направлениями и углами;

–предварительное решение треугольников;

–вычисление поправок за центрировку и редукцию;

–приведение измеренных направлений к центрам пунктов;

–составление схемы сети с приведенными углами;

–вычисление угловых невязок в треугольниках и установление их допустимости;

–оценка точности угловых измерений.

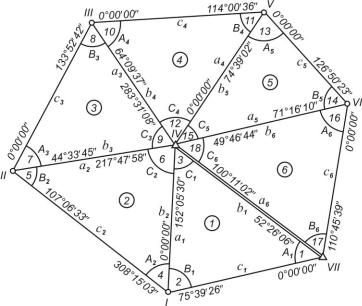
Рассмотрим порядок предварительных вычислений триангуляции 2 разряда на примере вычислительной обработки центральной системы

(рис. 6).

§26. Проверка результатов полевых измерений и вычислений

В полевых журналах проверяют все вычисления, включая нахождение

Рис.6. Схема сети с измеренными направлениями и углами

среднего арифметического из отсчетов, средних измеренных направлений и приведенных к нулю направлений; одновременно проверяют соблюдение установленных допусков в измерениях (незамыкание горизонта, колебание двойной коллимационной погрешности) по отдельным приемам и по всем приемам. В центрировочных листах проверяют значения элементов приведения и контрольного угла, а также правильность оформления листов. О результатах проверки делают отметки в полевых журналах и центрировочных листах.

Всводную ведомость наблюдений выписывают результаты измерения направлений всеми выполненными на пункте приемами; для суждения о качестве измерений для каждого приема указывают наибольшие значения разности повторных наблюдений на начальный пункт и колебания двойной коллимационной погрешности зрительной трубы. Затем находят средние значения направлений, приведенные к нулю, в образовании которых участвуют только приемы, удовлетворяющие требованиям инструкции.

По отклонениям отдельных значений направлений от среднего их значения выполняют оценку точности измеренных направлений по формулам Петерса.

Всводную ведомость средних значений направлений (табл.5) включают значения угловых и линейных элементов приведения направлений к центрам пунктов (центрировок и редукций).

			Таблица 5.
Элементы приведения и средние значения направлений
Пункт	Элементы	Наименование	Средние значения
Пункт	приведения	направления	направлений
	приведения	направления	направлений
		IV – V	0°00′00″
	l = 0,138 м	IV – VI	49°46′44″
п. IV	l1 = 0,095 м	IV – VII	100°11′02″
п. IV	= 80°30′ на п.V	IV – I	152°05′30″
	= 80°30′ на п.V	IV – I	152°05′30″
	1 =116°30′ на п.V	IV – II	217°47′58″
		IV – III	283°31′08″
	l = 0,119 м	V – VI	0°00′00″
	l1 = 0,042 м	V – VI	0°00′00″
п. V	l1 = 0,042 м	V – IV	74°39′02″
п. V	= 10°00′ на п.VI	V – IV	74°39′02″
	= 10°00′ на п.VI	V – III	114°00′36″
	1 =350°15′ на п. VI	V – III	114°00′36″
	1 =350°15′ на п. VI

Составляют схему с измеренными направлениями и углами (см. рис. 6). Углы между сторонами сети определяют как разности соответствующих направлений.

§27. Предварительное решение треугольников

Предварительное решение треугольников выполняют для нахождения длин сторон сети, которые необходимы для вычисления поправок за центрировку и редукцию.

Общие стороны смежных треугольников (IV –I, IV – II, IV – III и т.д.), называются связующими, остальные стороны (I – II, II – III, III – V и т.д.) – про-

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.68 Mб22960.pdf
#
15.11.20222.68 Mб32961.pdf
#
15.11.20222.69 Mб32962.pdf
#
15.11.20222.69 Mб22963.pdf
#
15.11.20222.69 Mб02964.pdf
#
15.11.20222.69 Mб52965.pdf
#
15.11.20222.7 Mб12967.pdf
#
15.11.20222.71 Mб22971.pdf
#
15.11.20222.72 Mб32972.pdf
#
15.11.20222.72 Mб12975.pdf
#
15.11.20222.72 Mб32976.pdf