2965

N) равным единице, т.е. p ij 1 p .

Согласно выражению (66) вес суммы углов j - го полигона

3. В сети N полигонов геометрического нивелирования получены невязки f h1 , fh2 , …, fhN в суммах превышений полигонов (ходов), периметры кото-

рых L1 , L2 , …, LN (в километрах).

Невязки fhi в полигонах представляет собой погрешности соответст-

вующих сумм превышений. Принимая вес превышения в полигоне длиной 1 км равным единице, имеем

pкм 2 1 , т.е. mкм .

mкм2

Число таких приведенных на 1 км превышений в j-ом полигоне равно Lj , а вес суммы превышений в этом полигоне

литься по формуле

41

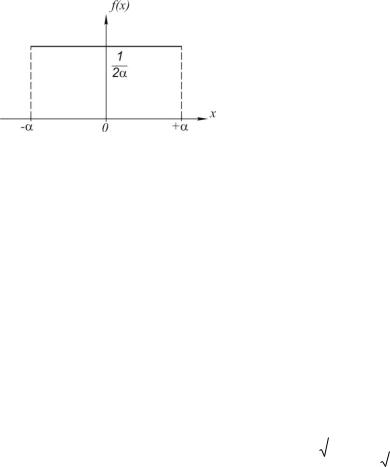
существенно отличаться от нормального. Так, например, погрешности отсчетов по шкале прибора или округление чисел при обработке результатов наблюдений подчиняются равномерному распределению, плотность которого выражается функцией

где – максимальное значение погрешности.

Как следует из графика функции (83), показанного на рис. 2, вероятность погрешности на всем интервале ; одинакова, т.е. f x c . Поскольку площадь прямоугольника под графиком будет равна

Дисперсия может быть получена как

D X M X 2 M (X ) 2 .

Тогда стандарт распределения, т.е. средняя квадратическая погрешность округления

где – абсолютное значение предельной погрешности округления.

Средняя квадратическая погрешность округления. В процессе вычис-

лений сохраняют определенное количество десятичных знаков приближенных чисел, отбрасывая ненужные, т.е. приближенные числа округляют до нужного знака. Сохраняемые десятичные знаки в приближенном числе называют значащими цифрами. Значащей цифрой может быть и нуль, если он расположен ме-

43

жду значащими цифрами, отличными от нуля, или сохраняется в конце числа в результате округления.

Процесс округления приближенного числа до некоторого разряда состоит в отбрасывании всех цифр, стоящих правее этого разряда. В вычислительной практике принято округлять числа по правилам Гаусса. Чтобы округлить число до n значащих цифр, отбрасывают все цифры, стоящие справа от n -ой значащей цифры. При этом следует соблюдать следующие требования:

–если первая из отброшенных цифр меньше 5, то оставшиеся десятичные знаки сохраняются без изменения (например, 72,4≈72);

–если первая из отброшенных цифр больше 5, то к последней оставшейся цифре прибавляется единица (84,56≈84,6);

–если первая из отброшенных цифр равна 5 и среди остальных отброшенных цифр имеются ненулевые, то последняя оставшаяся цифра увеличивается на единицу (64,51≈65);

–если первая из отброшенных цифр равна 5 и все остальные отброшенные цифры являются нулями, то последняя оставшаяся цифра

сохраняется неизменной, если она четная, и увеличивается на единицу, если она нечетная (например, 52,50≈52, а 53,50≈54).

Случайные погрешности округления обладают следующими свойствами: а) предельная погрешность округления 0,5 единицы последнего зна-

ка;

б) положительные и отрицательные погрешности округлений равновозможны;

в) среднее арифметическое из случайных погрешностей стремится к нулю при неограниченном возрастании их числа.

Случайное значение числа a может находиться с равной вероятностью в пределах от a 0,5t до a 0,5t , где t 2 − значение единицы последнего со-

храненного разряда. В единицах округляемого разряда возможны следующие погрешности округления:

−0,5; −0,4; −0,3; −0,2; −0,1; 0,0; +0,1; +0,2; +0,3; +0,4; +0,5.

Если их рассматривать как истинные погрешности, тогда средняя квадратическая погрешность округления будет

Принимая mo 0,3 и 0,5 , можно записать соотношения между ними:

1,7mo mo 3

или, как уже было доказано ранее,

44

Оценка точности арифметических действий с приближенными чис-

лами. Приведенные выше рассуждения относятся к одному округленному числу, тогда как в обработке наблюдений выполняются операции со многими числами. Суммарное воздействие таких чисел в процессе вычислений приводит к результатам, распределение погрешностей которых близко к нормальному. Это позволяет рассматривать погрешности арифметических действий с приближенными числами как средние квадратические погрешности функций независимо измеренных величин.

Погрешность округления алгебраической суммы приближенных чисел

При n 2 выражение (92) можно записать как

My пред 2 .

ух

Относительная предельная погрешность произведения n сомножителей

45

Предельные относительные погрешности функций возведения в степень и извлечения корня определяются соответственно выражениями:

В вычислительной практике для уменьшения влияния погрешностей округления промежуточные результаты обычно принимают на порядок точнее результатов измерений. Например, если измерения углов выполнены с погрешностью 0,5 – 1,0′, то промежуточные результаты вычисляют с точностью до 0,1′.

§17. Понятие о прямой и обратной задачах теории погрешностей измерений. Принцип равных влияний

При практическом использовании теории погрешностей измерений часто решают две принципиально разные задачи.

Впрямой задаче по известным погрешностям отдельных измерений находят погрешности окончательных результатов, являющихся функциями этих измерений. С прямой задачей связано также установление допустимых невязок.

С помощью обратной задачи можно установить средние погрешности

отдельных измерений для обеспечения заданной точности некоторой функции измеренных величин y f x1, x2 , , xn .

Воснову решения обратной задачи положено выражение

где M y − погрешность функции (допустимое значение конечного результата), m1, m2 , , mn − искомые средние квадратические погрешности измерений.

Поскольку уравнение (95) содержит несколько неизвестных, то обратная задача имеет множество решений. Подобную неоднозначность можно разрешить, накладывая дополнительные условия, которые основаны на различных принципах; наиболее простым из них является принцип равных влияний.

Сущность принципа равных влияний заключается в требовании равенства слагаемых в формуле средней квадратической погрешности функции общего вида

46

получим

Приведенное соотношение позволяет вычислить значения средних квадратических погрешностей аргументов по заданной точности функции.

Пример. Превышение между точками, определенное методом тригонометрического нивелирования, рассчитано по формуле h D sin v . В результате измерений получено наклонное расстояние D 200 м и угол наклона v 5 . Величина превышения h должна быть получена со средней квадратической погрешностью M h 0,10 м. С какой точностью должны быть измерены наклонное

расстояние D и угол наклона v ? Погрешность функции h D sin v

При условии, что влияние погрешностей измерений расстояния и угла наклона на величину средней квадратической погрешности превышения одина-

ково, можно записать

Подставляя в полученные выражения численные значения известных величин, получим:

47

Следовательно, в рассматриваемом примере для обеспечения требуемой точности определения превышения ( M h 0,10 м) измерение угла наклона мож-

но выполнять теодолитом типа Т30, а расстояние измерять с помощью нитяного дальномера.

48

Раздел второй Уравнивание геодезических сетей сгущения и съемочных сетей

Глава 5. ОБЩИЕ СВЕДЕНИЯ ОБ УРАВНИВАНИИ ГЕОДЕЗИЧЕСКИХ

СЕТЕЙ

§ 18. Сущность уравнительных вычислений. Метод наименьших квадратов

В геодезических сетях для контроля и оценки качества измерений, а также для повышения их точности наряду с необходимыми всегда выполняют избыточные измерения. Избыточные измерения необходимы для контроля, повышения точности результатов измерений и оценки их качества.

Необходимые и избыточные измерения в сети находятся в определенных математических соотношениях, которые в результате обработки результатов измерений должны быть удовлетворены. Кроме того, при развитии геодезических сетей используют также избыточные исходные данные (координаты исходных пунктов, длины базисов, дирекционные углы линий), что приводит к появлению дополнительных геометрических условий.

Ввиду присутствия в результатах измерений (как необходимых, так и избыточных) неизбежных случайных погрешностей возникающие в сети геометрические условия не соблюдаются точно, что приводит к появлению невязок, которые должны быть устранены путем введения поправок в измеренные величины.

Избыточные измерения позволяют получить определяемые величины несколькими путями, при этом значения одной и той же величины будут различны между собой, т.е. возникает неоднозначность решения задачи. В результате уравнивания каждая определяемая величина должна иметь одно и то же значение независимо от пути ее вычисления. Таким образом, уравнивание сети есть вычислительный процесс по распределению невязок, т.е. нахождение системы поправок, которая доставляет наилучшие значения измеренных и искомых величин, а также оценка их точности. Наилучшими значениями будем считать величины, наиболее близкие к действительным (истинным) их значениям.

Так как истинные погрешности в измерениях не известны и эти погрешности являются случайными, то логично поставить при уравнивании такое условие, чтобы найденные поправки в измерения (определения) как можно меньше искажали бы результаты измерений, т.е. воспользоваться принципом наименьших квадратов

Лежандром для обработки результатов наблюдений и получил развитие в работах К.Гаусса, русского математика А.А. Маркова и др.

49

Уравнительные вычисления с применением принципа наименьших квад-

ратов называют уравниванием по методу наименьших квадратов. Теоретически доказано, что соблюдение условия (97) при уравнивании приводит к наилучшим оценкам определяемых величин. В этом случае уравнительные вычисления называют строгими.

Строгие способы уравнивания обеспечивают соблюдение трех требо-

ваний:

а) выполнение всех геометрических условий в сети; б) нахождение наиболее надежных значений измеренных величин под

условием p 2 min ;

в) оценку точности результатов измерений и их функций, т.е. уравненных элементов сети.

Строгие методы уравнивания позволяют получать наилучшие (с минимальными средними квадратическими погрешностями) результаты, эффективно совмещают в одной программе процессы уравнивания, оценки точности и реализации заключительных контролей качества уравненных результатов, более удобны для программирования задач при уравнивании с использованием ЭВМ.

Для уравнивания геодезических построений используют параметрический и коррелатный способы. При коррелатном способе поправки отыскивают непосредственно к измеренным величинам, а при параметрическом – к их функциям. Оба этих способа уравнивания являются строгими и приводят к равноценным результатам. Выбор того или иного способа уравнивания определяется в основном числом исходных данных и избыточных измерений, а также с учетом использования оптимального алгоритма решения задачи. В настоящее время уравнивание геодезических сетей выполняют на ЭВМ по параметрическим алгоритмам и программам, основанным на итерационных методах, позволяющих решать системы уравнений с некоторой заранее заданной точностью с помощью сходящихся бесконечных процессов, т.е. последовательными приближениями.

Наряду со строгими методами существуют приближенные (упрощенные) способы уравнивания, в которых соблюдаются геометрические условия в сети, а другие требования выполняются частично.

В практической деятельности инженеров землеустройства и земельного кадастра довольно часто возникает необходимость уравнивания ограниченных по площади геодезических систем с небольшим числом неизвестных. Использование при этом современной измерительной техники (светодальномеров, электронных теодолитов и тахеометров, цифровых нивелиров и т.п.) позволяет существенно повысить точность измерений и уменьшить величины невязок. В таких случаях уравнительные вычисления могут выполняться с использованием функциональных микрокалькуляторов упрощенными способами, дающими результаты, весьма близкие к результатам строгого уравнивания. Существенным недостатком упрощенных способов уравнивания является невозможность пол-

50