2965

цию плотности нормального распределения, которая может быть представлена в виде

Плотность нормального распределения погрешности, описываемая выра-

жением (6), называют уравнением погрешностей или кривой Гаусса.

Кривая погрешностей, представленная графически на рис. 1, обладает следующими свойствами:

1.Ордината y f ( ) при любых значениях не принимает отрицательных значений и не обращается в нуль, т.е. y > 0.

2.Кривая погрешностей симметрична относительно оси Oу, так как значения ординат для одинаковых по абсолютной величине положительных и отри-

4.Кривая погрешностей имеет две точки перегиба (слева и справа от оси Оу) при m .

5.Касательные к кривой в точках перегиба пересекаются с осью абсцисс

вточках 2m .

Принципиальное отличие средней квадратической погрешности m от среднего квадратического отклонения σ состоит в том, что σ – постоянная теоретическая величина, характеризующая бесконечную совокупность данного вида измерений, а погрешность m является величиной эмпирической, получаемой при ограниченном числе испытаний. С увеличением числа испытаний m . Следовательно, сред-

няя квадратическая погрешность m является оценкой (приближенным значением) неизвестного среднего квадратического отклонения σ.

Поскольку ряд измерений, из которого находится средняя квадратическая погрешность m, является конечным, то значение самой этой погрешности определится с некоторой погрешностью

11

Величина mm является оценкой точности определения средней квадра-

тической погрешности m.

При большом числе измерений существуют устойчивые зависимости между рассмотренными критериями точности:

Наряду со средней квадратической погрешностью другой важной характеристикой точности измерений является предельная погрешность, т.е. такое значение случайной погрешности, появление которого при данных условиях измерений маловероятно. Из анализа нормального распределения случайной погрешности (см. рис. 1) следует, что случайная погрешность измерения может превысить среднюю квадратическую примерно в 32 случаях из 100, удвоенную среднюю квадратическую погрешность – в 5 случаях из 100, утроенную – в 3 случаях из 1000. Следовательно, достаточно маловероятно, что случайная погрешность измерения превысит утроенную среднюю квадратическую. Поэтому при топографо-геодезических работах за предельную допустимую величину погрешности обычно принимают утроенную среднюю квадратическую погрешность, т.е.

mпред 3 m .

При выполнении ответственных измерений предельную допустимую погрешность ограничивают величиной

mпред 2 m .

Величины предельных допустимых погрешностей приводятся в инструкциях по производству геодезических измерений и служат критериями для отбраковки результатов измерений, имеющих погрешности более допустимых. Такие погрешности считают грубыми, и соответствующие измерения должны быть выполнены заново.

По форме числового выражения все погрешности разделяют на абсолют-

ные и относительные.

Абсолютные (средние, средние квадратические, вероятные и предельные) погрешности выражаются в тех же единицах, что и измеряемые величины; обычно они используются для оценки точности измерений, не зависящих от значения измеряемой величины (например, от величины измеряемого угла). Однако абсолютные погрешности не всегда наглядно характеризуют точность измерений, особенно результатов непосредственных измерений линейных величин, погрешности которых зависят от длин линий. В таких случаях используют понятие относительной погрешности.

Относительной погрешностью называется отношение абсолютной погрешности к измеренной величине. Она выражается правильной дробью, чис-

12

литель которой равен единице. Например, если линия длиной l измерена с абсолютной средней квадратической погрешностью ml, то относительная погрешность

Ниже приведен пример оценки результатов равноточных измерений, т.е. нахождение числовых характеристик точности измерений.

Пример. Длина линии измерена рулеткой 4 раза (табл. 1). Из измерений этой же линии высокоточным светодальномером известна истинная (действительная) длина линии L=181,246м. Требуется найти среднюю квадратическую

§5. Средние квадратические погрешности функций измеренных величин

В геодезической практике часто значения искомых величин (например, координат точек, превышений и т.п.) находят по результатам непосредственных измерений углов, линий и др. Очевидно, что если непосредственные измерения (аргументы) сопровождаются случайными погрешностями, то и результаты косвенных измерений как функции этих аргументов будут иметь погрешности. При этом величина средней квадратической погрешности функции измеренных величин зависит не только от погрешностей аргументов, но и от вида функции, связывающей непосредственные измерения с косвенными.

13

Пусть задана функция общего вида y=f(x1, x2, ... , xn), аргументы которой независимо измерены со средними квадратическими погрешностями m1, m2, ... ,

mn.

Выразим величины функции и аргументов через их истинные значения и погрешности в виде

У у f X1 x1, X2 x2 , , Xn xn . (11)

Поскольку погрешности х1, х2,…, хn малы по сравнению с измеренными величинами, то, разложив выражение (11) в ряд Тейлора, можно ограничиться при разложении членами, содержащими только первые степени погрешностей, т.е.

Переход от соотношения (11) к выражению (12) называется приведением функции к линейному виду.

Поскольку У f Х1 , Х2 ,..., Хn , то из уравнения (12) имеем

Для ряда из k измерений можно получить k аналогичных равенств, просуммировав которые получим

14

Переходим от истинных погрешностей к средним квадратическим погрешностям, учитывая, что согласно формуле Гаусса (4)

т.е. квадрат средней квадратической погрешности функции общего вида независимых аргументов равен сумме квадратов произведений частных производных по каждому аргументу на средние квадратическое погрешности соответствующих аргументов.

Все другие функции можно рассматривать как частные случаи функции общего вида. Рассмотрим погрешности некоторых функций измеренных величин.

1. Алгебраическая сумма измеренных величин y x1 x2 ... xn , причем x1 , x2 ,..., xn определены со средними квадратическими погрешностями m1, m2, … , mn.

Согласно формуле (17) имеем

15

Исходя из выражений (18) и (19), формулу средней квадратической погрешности линейной функции можно записать в виде

Ниже приведены примеры применения этих выражений для решения некоторых геодезических задач.

Пример 1.

Угол измерен двумя полуприемами, в результате чего получены значения угла КЛ и КП . Средняя квадратическая погрешность измерения угла в полу-

скою погрешность m угла, измеренного полным приемом.

Выражение для вычисления среднего значения угла можно записать в виде

21 КЛ 21 КП .

Согласно формуле (23)

16

Пример 2.

Длина штриховой мерной ленты Л3-20 определена на компараторе со средней квадратической погрешностью mк=1мм. Этой лентой измерена линия длиной D=164,15 м. Требуется определить среднюю квадратическую погрешность измеренной линии, обусловленную погрешностью компарирования.

При измерении линии число укладок ленты в расстояние D является постоянным числом

Длина D l n 8,2 l .

С учетом формулы (21)

mD n mk 8, 2 1мм 8, 2мм 8мм.

Пример 3.

Длины сторон a = 62м и b = 46м земельного участка прямоугольной формы измерены с относительной погрешностью fотн=1:1000. Найти абсолютную и относительную средние квадратические погрешности определения площади участка.

Площадь участка S = аb = 62 · 46=2852м2.

Поскольку fотн maa mbb 10001 , то абсолютные погрешности измерения

длин сторон mа = 0,062м, mb = 0,046м.

Согласно формуле (20)

Пример 4.

Найти погрешность определения приращения координаты x , вычисленного по формуле x = d cos , если длина стороны d =150,0 м измерена со средней квадратической погрешностью m d =0,1м, а дирекционный угол 60o 02 определен с погрешностью m 1′.

Исходя из выражения (17)

17

§6. Принцип среднего арифметического и его средняя квадратическая погрешность

Пусть в результате равноточных измерений величины, истинное значение Х которой известно, получен ряд измеренных значений

l1, l2, ..., ln.

Как отмечалось ранее, разности между каждым измеренным значением l и истинным X представляют собой истинные погрешности

Δ1=l1−X; Δ2=l2 −Χ; …; Δn=ln − Χ. (24)

С учетом того, что грубые и систематические погрешности исключены из результатов измерений, истинные погрешности можно считать случайными.

Сложив почленно все левые и правые части равенства в (24), получим

l Xn .

18

Правая часть выражения (26) представляет собой линейную функцию не-

зависимых аргументов l1 , l2 ,..., ln. Тогда в соответствии с формулой (23) средняя квадратическая погрешность среднего арифметического будет

т.е. средняя квадратическая погрешность арифметической середины в 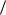n раз меньше средней квадратической погрешности отдельного измерения.

Анализ выражения (28) показывает, что с увеличением числа измерений повышается точность определения среднего арифметического из результатов этих измерений. Однако чрезмерное увеличение числа измерений в большинстве случаев является нецелесообразным, так как при этом преобладающее влияние оказывают остаточные систематические погрешности, препятствующие повышению точности окончательного результата. Дальнейшее повышение точности результатов измерений может быть обеспечено путем применения более совершенных приборов и методов измерений.

§7. Средняя квадратическая погрешность отдельного измерения, вычисленная по уклонениям от среднего арифметического

Приведенная ранее формула Гаусса (4) применима в весьма редких случаях, когда известно истинное значение измеряемой величины X. В практике по результатам измерений обычно определяют среднее арифметическое (вероятнейшее значение) величины. В этом случае среднюю квадратическую погрешность отдельного результата из ряда равноточных измерений можно вычислить по их уклонениям от среднего арифметического x , которые являются вероят-

нейшими погрешностями измерений.

Уклонением u называется разность между результатом отдельного

измерения и среднего арифметического из ряда равноточных измерений

При уравнивании результатов измерений в геодезических вместо уклонений (вероятнейших погрешностей) иi принято пользоваться вероятнейшими поправками i иi

19

Уклонения обладают следующими свойствами:

1.Алгебраическая сумма уклонений равна нулю при любом числе измере-

ний, т.е. и 0 .

Для ряда равноточных измерений можно записать:

u1 l1 x ; u2 l2 x ; … ; un ln x .

После сложения левых и правых частей равенств получим

u l xn .

Поскольку l xn , то u 0 .

Это свойство уклонений используют для контроля правильности вычис-

где х − переменная величина, li – результаты измерений, ui − уклонения резуль-

татов измерений от выбранной величины x.

Для проверки функции на минимум следует взять ее производную и приравнять к нулю, т.е.

отдельных измерений от среднего арифметического надо объединить значения истинной и вероятнейшей погрешностей.

20