
2945
.pdfНа сегодняшний день руководители отечественных предприятий вкладывают в развитие трудового потенциала меньше средств, чем в развитых зарубежных странах. Так, например, в США предприниматели совокупно расходуют на подготовку персонала более 238 млрд долл. в год, а общие затраты на общественное образование составляют 310 млрд долл. в год. На каждый доллар, вложенный в развитие производства в США, приходится 85 центов, вложенных в развитие рабочей силы. В России на каждый рубль, вложенный в развитие средств производства, приходится 15 копеек, направленных на развитие рабочей силы. Разница очевидна.
Заключение
Сегодняшняя ситуация на рынке труда отражает глобальные направления развития бизнеса, поэтому именно сейчас, как в любом переходном периоде, можно получить весомое конкурентное преимущество, если выстроить управление персоналом в соответствии с новыми тенденциями.
Концепция кадровой политики и применение современных методов и мотивации ориентируется на профессиональную подготовку кадров, внедрение системы ротации кадров на предприятиях, материальное стимулирование. Но эти задачи невозможно решить, не изменив отношение организаций к своим кадрам, и изменения должны быть не только на бумаге, они должны произойти и в сознании каждого руководителя на уровне его конкретных действий.
Нельзя хорошо управлять, не зная людей, не зная их возможностей, способностей, квалификации не только в производственной сфере, но и их психологических особенностей, которые необходимы для решения как производственных, так и социальных задач. Сама профессия руководителя аккумулирует большой потенциал научного знания о человеке, о его взаимодействии с другими людьми, окружающей производственной средой и прежде всего о управлении, психологии, социологии, праве, экономике. Важнейшая ценность практики управления персоналом состоит в том, что при продуманной ее организации она способна обеспечивать профессионализм персонала, творческое отношение его к труду.
Библиографический список
1.Армстронг, М. Практика управления человеческими ресурсами. / Пер. с англ., под ред. С.М. Мордовина. – СПб.: Питер, 2004.- 831с.
2.Анурова, Н.И.. Персонал в торговой организации. Как создать профессиональную команду. М,. 2003 -234с.
3.Блинов, А.А. Мотивация персонала корпоративных структур/А. Блинов//Маркетинг.- 2001.- № 1. - С. 88-101.
4.Верховин, В.И. Мотивация труда работников в условиях современного производства. В.И. Верховин - М.: Дело, 2002 - 324с.
5.Веснин, В.Р. Практический менеджмент персонала /В.Р. Веснин. - М.: Юрист, 2001. – 661
с.
6.Егоршин, А.П.Управление персоналом /А.П. Егоршин. - Н.Новгород: НИМБ, 2004 – 432с.
7.Каверин, С.Б. Мотивация труда. / С.Б. Каверин М.: Дело, 2004 – 354с.
8.Махорт, Н. Проблема мотивации в трудовой деятельности/ Н. Махорт//
Управление персоналом.- 2002.
9.Ладанов, И.Д. Практический менеджмент./ И.Д. Ладанов - М.2002 – 324с.
10.Основы управления персоналом: учеб. пособие./под ред. Б.М. Генкина; М.: Изд-во Высш. шк., 2002435с.
11.Для подготовки данной работы были использованы материалы с сайта http://www.gd.ru.
83

УДК 658.1-50
Воронежский государственный архитектурно-строительный университет к. техн. н., доц. каф. "Управление строительством" В.Л. Порядина Россия, г. Воронеж, тел.: 276-40-07
В. Л. Порядина
РЕШЕНИЕ ЗАДАЧ УПРАВЛЕНИЯ ПРОЕКТАМИ ПРИ ЗАВИСИМОСТЯХ РЕКОМЕНДАТЕЛЬНОГО ТИПА МЕТОДОМ ДИХОТОМИЧЕСКОГО ПРОГРАМ-
МИРОВАНИЯ
Рассмотрен метод решения задач дискретной оптимизации – метод дихотомического программирования. Идея метода заключается в возможности представления функции в виде суперпозиции более простых функций. Метод дихотомического программирования в данной работе применён для решения:
-задачи построения календарного плана с минимальной продолжительностью проекта; -задачи построения календарного плана с минимальными дополнительными затратами;
-задачи построения календарного плана заданной продолжительности при минимальном увеличении затрат.
V. L. Poryadina
SOLUTION OF PROBLEMS IN PROJECT MANAGEMENT BY TYPE OF RECOMMENDATION DEPENDING DICHOTOMOUS PROGRAMMING
This article describes the method for solving discrete optimization problems - dichotomous programming method. The idea of the method is the ability to view functions as a superposition of simpler functions.
Dichotomous programming method applied in this paper for the following project management tasks:
-task of building a schedule with a minimum duration of the project;
-task of building a schedule with minimal additional cost;
-task of building a schedule predetermined duration with a minimum increase in cost.
Управление проектами – это раздел науки управления в социальных и экономических системах. Каждый проект имеет некоторую протяженность во времени и состоит из некоторого количества работ. Естественно возникает задача распределения ресурсов по работам проекта наиболее эффективным способом. Работы в проекте могут быть связаны и независимы. Зависимость между работами (или ее отсутствие) может быть представлено в виде сетевой модели. Следовательно, возникает задача распределения ресурсов на сетях.
Существуют 4 вида зависимости между работами проекта:
1)старт – финиш;
2)старт – старт;
3)финиш – старт;
4)финиш – финиш.
Наиболее часто встречаемая зависимость – финиш – старт.
Эти зависимости имеют обязательный характер, т.е. должны выполняться обязательно (их называют жесткими зависимостями).
Однако на практике часто встречаются ситуации, когда эти зависимости носят не обязательный, а рекомендательный характер, другими словами, они могут нарушаться, но их нарушение ведет к определенным потерям: либо к увеличению продолжительности работ, либо к росту затрат на реализацию проекта.
©Порядина В.Л.,2016
84
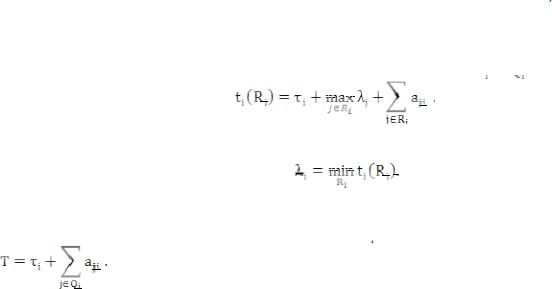
Пусть имеется проект из n работ, мягкие зависимости между которыми описаны сетевым графиком.
Вершины сетевого графика соответствуют работам проекта, в верхней половине вершины указан номер работы, а в нижнем – ее продолжительность. Дуги соответствуют мягким зависимостям между работами. Для каждой дуги заданы два числа аij и bij.
1.аij ≥0 определяет увеличение продолжительности работы j, т.е. если работа j начата до окончания работы i.
2.bij≥0 определяет увеличение затрат на выполнение работы j, если завершение работы ij нарушается.
Для описания задачи возможны 3 постановки задач.
1.Пусть заданы только числа аij≥0 (bij 0). Требуется определить календарный план с минимальной продолжительностью проекта.
0). Требуется определить календарный план с минимальной продолжительностью проекта.
2.Пусть заданы только числа bij≥0 (аij=0). Требуется определить календарный план с минимальными дополнительными затратами.
3.Пусть заданы оба числа аij ≥0 и bij≥0. Требуется определить календарный план, при котором проект выполняется за время Т, а увеличение затрат минимально.
Решение задачи построения календарного плана с минимальной продолжительностью проекта
Присваиваем всем работам сетевого графика начальный индекс λi=τi, i= . Рассматриваем каждую работу i. Обозначим через Qi – множество работ, предшествующих работе i, то есть в сетевом графике существует дуга (j, i) для j Qi . Обозначим через mi – число дуг, заходящих в вершину i (число элементов множества Qi). Рассмотрим все подмножества из mi. Для каждого подмножества содержащего вершины
. Рассматриваем каждую работу i. Обозначим через Qi – множество работ, предшествующих работе i, то есть в сетевом графике существует дуга (j, i) для j Qi . Обозначим через mi – число дуг, заходящих в вершину i (число элементов множества Qi). Рассмотрим все подмножества из mi. Для каждого подмножества содержащего вершины 




 вычисляем
вычисляем
Определяем новый индекс вершины i:
Алгоритм заканчивается, когда все индексы установятся. Конечность алгоритма следует из того, что последовательность индексов для каждого i является возрастающей. С другой стороны индексы 
 ограничены величиной
ограничены величиной
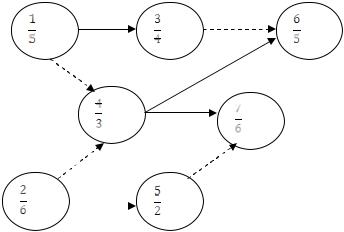
Пример. Пусть имеется проект из 10 работ, зависимости между которыми описаны сетевым графиком. Вершины сетевого графика соответствуют работам проекта (Рис. 1). В верхней половине вершины указан номер работы, в нижнем – ее продолжительность. Для каждой дуги задано число аij≥0, которое определяет увеличение продолжительности работы j, если зависимость i, j нарушается. Требуется определить календарный план с min продолжительностью проекта.
85
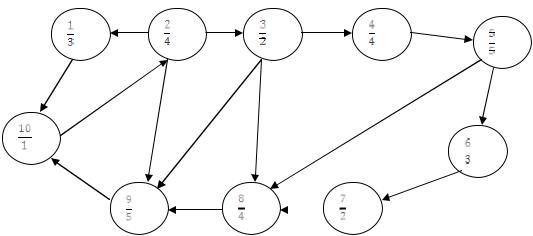
Рис.1
4 |
1 |
6 |
4 |
8 |
|
|
|
2 |
||
1 |
9 |
|
4 |
8 |
|
|
|
|
|
|
|||
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|
53
1.τ1=3; τ2=4; τ3=2; τ4=4; τ5=5; τ6=3; τ7=2; τ8=4; τ9=5; τ10=1.
2.Рассмотрим первую вершину. В нее заходит 1 дуга:
зависимость (2;1) не учитывается: t1= τ1+a21=3+4=7; зависимость (2;1) учитывается:
t1= τ1+ τ2=3+4=7, следовательно, λ1=7. Рассмотрим вторую вершину:
зависимость (10;2) не учитывается: t2= τ2+a10;2=4+1=5; зависимость (10;2) учитывается: t2= τ2+ τ10=4+1=5, следовательно, λ2=5.
Рассмотрим третью вершину:
зависимость (2;3) не учитывается: t3= τ3+a23=2+1=3; зависимость (2;3) учитывается: t3= τ3+ λ2=2+5=7, следовательно, λ3=3.
Рассмотрим четвертую вершину:
зависимость (3;4) не учитывается: t4= τ4+a34=4+6=10; зависимость (3;4) учитывается: t4= τ4+ λ3=4+3=7, следовательно, λ4=7.
Рассмотрим пятую вершину:
зависимость (4;5) не учитывается: t5= τ5+a45=5+4=9; зависимость (4;5) учитывается: t5= τ5+ λ4=5+7=12, следовательно, λ5=9.
Рассмотрим шестую вершину:
зависимость (5;6) не учитывается: t6= τ6+a56=3+2=5; зависимость (5;6) учитывается: t6= τ6+ λ5=3+9=12, следовательно, λ6=5.
Рассмотрим седьмую вершину:
зависимость (6;7) не учитывается: t7= τ7+a67=2+3=5; (6;7) учитывается: t7= τ7+ +λ6=2+5=7, следовательно, λ7=5.
Рассмотрим восьмую вершину. В нее заходят 3 дуги:
(7;8) не учитывается; (5;8) не учитывается; (3;8) не учитывается: t8= τ8+ a78+ a58+ +a38=4+3+8+4=19;
(7;8) учитывается; (5;8) не учитывается; (3;8) не учитывается: t8=τ8+λ7+a58+ +a38=4+5+8+4=21;
(7;8) не учитывается; (5;8) учитывается; (3;8) не учитывается: t8=τ8+a78+λ5+ +a38=4+3+9+4=20;
(7;8) не учитывается; (5;8) не учитывается; (3;8) учитывается: t8=τ8+a78+a58+ +λ3=4+3+8+3=18;
(7;8) учитывается; (5;8) учитывается; (3;8) учитывается: t8= τ8+ max(λ7; λ5; λ3)=4+max (5;9;3)=13;
(7;8) учитывается; (5;8) учитывается; (3;8) не учитывается: t8= τ8+ max (λ7; λ5)+ +a38=4+9+4=17;
(7;8) учитывается; (5;8) не учитывается; (3;8) учитывается: t8= τ8+ max (λ7; λ3)+
86

+a58=4+5+8=17;
(7;8) не учитывается; (5;8) учитывается; (3;8) учитывается: t8= τ8+ a78+ max (λ5; λ3)=4+3+9=16, следовательно, λ8=13;
Рассмотрим девятую вершину:
(2;9) не учитывается; (3;9) не учитывается; (8;9) не учитывается: t9=τ9+ a29+ a39+ +a89=5+9+7+5=26;
(2;9) учитывается; (3;9) не учитывается; (8;9) не учитывается: t9=τ9+λ2+a39+ +a89=5+5+7+5=22;
(2;9) не учитывается; (3;9) учитывается; (8;9) не учитывается: t9=τ9+a29+λ3+ +a89=5+9+3+5=22;
(2;9) не учитывается; (3;9) не учитывается; (8;9) учитывается: t9= τ9+ a29+ a39+ +λ8=5+9+7+13=34;
(2;9) учитывается; (3;9) учитывается; (8;9) учитывается: t9= τ9+ max (λ2; λ3; λ8)=5+ +max (5;3;13)=18;
(2;9) учитывается; (3;9) учитывается; (8;9) не учитывается: t9= τ9+ max (λ2; λ3)+ +a89=5+5+5=15;
(2;9) учитывается; (3;9) не учитывается; (8;9) учитывается: t9= τ9+ max (λ2; λ8)+ +a39=5+13+7=25;
(2;9) не учитывается; (3;9) учитывается; (8;9) учитывается: t9= τ9+max (λ3; λ8)+a29=5+13+9=27, следовательно, λ9=15;
Рассмотрим десятую вершину:
(1;10) не учитывается; (9;10) не учитывается: t10= τ10+a1;10+a9;10 =1+8+6=15; (1;10) учитывается; (9;10) не учитывается: t10= τ10+ λ1+ a9;10 =1+7+6=14; (1;10) не учитывается; (9;10) учитывается: t10= τ10+ a1;10+ λ9=1+8+15=24;
(1;10) учитывается; (9;10) учитывается: t10= τ10+ max (λ1; λ9)=1+15=16, следовательно, λ10=14.
Замечание. Число вариантов можно сократить, если дуги множества 

 рассматривать в очередности убывания
рассматривать в очередности убывания 

 В этом случае, если мы учитываем дугу
В этом случае, если мы учитываем дугу  , то можно сразу учесть все дуги с меньшими или равными
, то можно сразу учесть все дуги с меньшими или равными 






 . В нашем случае достаточно рас-
. В нашем случае достаточно рас-
смотреть 4 варианта. В общем случае, если в вершину  заходит mi дуг, достаточно рас-
заходит mi дуг, достаточно рас-
смотреть mi+1.
Проверим корректировку индексов вершин в том же порядке. Рассмотрим первую вершину. Имеем одну заходящую дугу, т.е. λ1= τ1+min (a21; λ2)=3+ min(4;5)=7.
Рассмотрим вторую вершину:
λ 2= τ2+min (a10;2; λ10)=4+ min(1;12)=5. Рассмотрим третью вершину:
λ 3= τ3+min (a32; λ2)=2+ min(1;5)=3. Рассмотрим четвертую вершину: λ 4= τ4+min (a34; λ3)=4+ min(6;3)=7. Рассмотрим пятую вершину:
λ 5= τ5+min (a45; λ4)=5+ min(4;7)=9. Рассмотрим шестую вершину:
λ 6= τ6+min (a56; λ5)=3+ min(2;9)=5. Рассмотрим седьмую вершину:
λ 7= τ7+min (a67; λ6)=2+ min(3;5)=5. Рассмотрим восьмую вершину:
λ 8= τ8+min (9; 4+9; 8+5; 3+9)=13. Рассмотрим девятую вершину:
λ 9= τ9+min (13; 9+13; 7+5; 5+5)=15. Рассмотрим десятую вершину:
λ 10= τ10+min (15; 8+15; 6+7;)=14.
87
Величина индекса не изменилась, так как индексы установлены, то алгоритм за- |
||||
кончен. |
|
|
|
|
Теорема. Установившиеся значения индексов |
определяют минимальные ранние |
|||
сроки завершения работ. |
|
|
|
|
Применение метода дихотомического программирования для построения |
||||
календарного плана с минимальными дополнительными затратами |
||||
Применим метод дихотомического программирования к решению задачи 2. |
||||
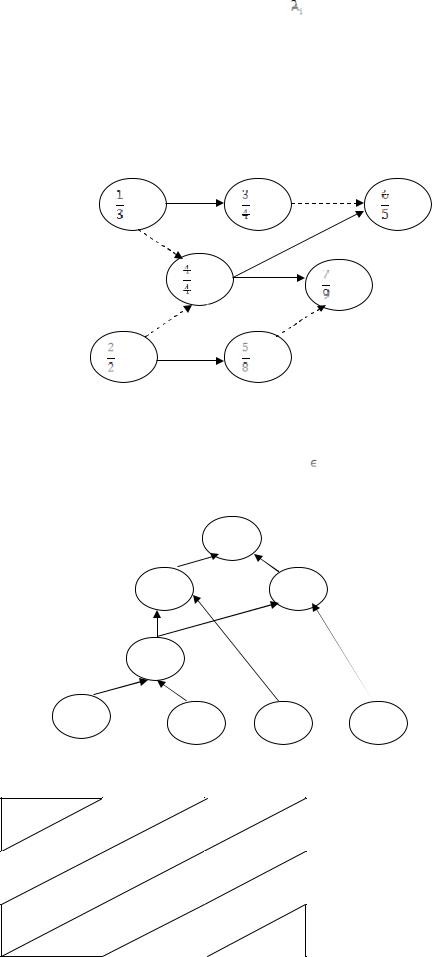
Рассмотрим сетевой график без контуров Рис. 2, в котором некоторое множество Q |
||||
зависимостей являются мягкими, мягкие зависимости показаны пунктиром. |
||||
|
|
|
|
(2) |
|
(8) |
|
|
|
|
(15) |
|
(5) |
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
При построении дихотомического представления естественно учитывать только |
||||
моменты окончания тех работ j, которые связаны с мягкими зависимостями, хотя бы с од- |
||||
ной работой, т.е. существует работа i такая, что дуга (i; j) Q. |
||||
Дихотомическое представление сетевого графика имеет вид, представленный на |
||||
Рис. 3: |
|
|
|
|
|
|
Т |
|
|
|
Т6 |
|
Т7 |
|
|
Т4 |
|
|
|
(1;2) |
(2;4) |
|
(3;6) |
(5;7) |
|
|
|||
|
|
Рис. 3 |
|
|
Построим соответствующие матрицы для Т4, Т6, Т7. |
||||
0 |
6 |
4 |
|
|
8 |
8 |
|
23 |
|
Т4= |
|
|
|
|
3 |
7 |
7 |
|
|
0 |
0 |
|
15 |
|
Т1 |
2 |
0 |
|
|
Т2 |
0 |
88 |
15 |
|
|
0 |
12 |
11 |
|
9 |
|
2 |
|
2 |
6 |
13,5 |
Т6= |
|
|
|
|
|
|
7 |
12 |
12 |
|
12 |
|
0 |
|
0 |
4 |
11,5 |
|
Т3 |
7 |
6 |
|
4 |
|
Т4 |
|
0 |
4 |
11,5 |
|
0 |
16 |
15 |
|
13 |
Т7= |
5 |
|
5 |
9 |
16,5 |
|
10 |
19 |
19 |
|
19 |
|
0 |
|
0 |
4 |
11,5 |
|
Т5 |
7 |
6 |
|
4 |
|
Т4 |
|
0 |
4 |
11,5 |
Теперь можно решить задачу оптимизации дополнительных затрат для любого Т. 1. Возьмем Т≤19.
Из матрицы Т7 получаем Т4=7 и Т5=10, следовательно, зависимость (5;7) учитывается. Из матрицы Т6 получаем Т4=7 и Т3=7, следовательно, зависимость (3;6) учитывается.
Из матрицы Т4 получаем Т2=2 и Т1=3, следовательно, зависимости (1;4) и (2;4) учитываются.
Таким образом, все зависимости учитываются и дополнительные затраты равны
нулю.
2. Возьмем Т≤16.
Из матрицы Т7 получаем Т4=7 и Т5=0, следовательно, зависимость (5;7) не учитывается. Из матрицы Т6 получаем Т4=7 и Т3=0, следовательно, зависимость (3;6) не учитывается. Из матрицы Т4 получаем Т2=6 и Т1=3, следовательно, зависимости (1;4) учитывается, а (2;4) не учитываются.
Таким образом, зависимости (5;7), (3;6), (2;4) не учитываются и дополнительные затраты равны 22.
3.Возьмем Т≤15.
Из матрицы Т7 получаем Т4=6 и Т5=0, следовательно, зависимость (5;7) не учитывается. Из матрицы Т6 получаем Т4=6 и Т3=0, следовательно, зависимость (3;6) не учитывается. Из матрицы Т4 получаем Т2=2 и Т1=0, следовательно, зависимость (1;4) не учитывается, а (2;4) учитывается.
Таким образом, зависимости (5;7), (3;6), (1;4) не учитываются и дополнительные затраты равны 15.
4.Возьмем Т≤13.
Из матрицы Т7 получаем Т4=7 и Т5=0, следовательно, зависимость (5;7) не учитывается. Из матрицы Т6 получаем Т4=4 и Т3=0, следовательно, зависимость (3;6) не учитывается. Из матрицы Т4 получаем Т2=0 и Т1=0, следовательно, зависимости (1;4) и (2;4) не учитываются.
Таким образом, зависимости (5;7), (3;6), (1;4), (2;4) не учитываются и дополнительные затраты равны 30.
89
Построение календарного плана заданной продолжительности при минимальном увеличении затрат
Обобщим метод дихотомического программирования на задачу 3.
Изменение состоит в том, что при формировании матриц дихотомического представления необходимо учитывать увеличение продолжительности работ.
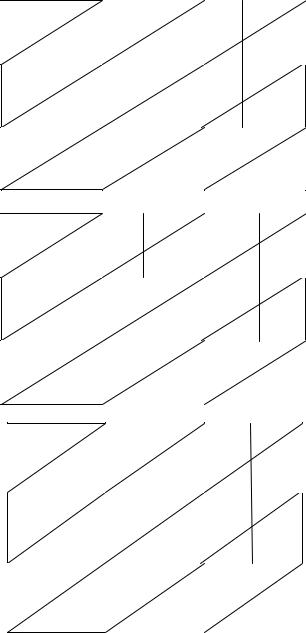
Рассмотрим метод на примере сетевого графика Рис. 4.
(5)
(6)
(12)(2)
Рис. 4
Применим следующие значения аiϳ для мягких зависимостей:
(i, ϳ) |
(1;4) |
(2;4) |
(3;6) |
(5;7) |
аiϳ |
3 |
2 |
2 |
1 |
90
Построим соответствующие матрицы для Т4, Т6, Т7. |
||||
|
0 |
9 |
9 |
|
|
8 |
8 |
23 |
|
|
3 |
7 |
9 |
|
|
0 |
0 |
15 |
|
Т4= |
|
|
|
|
|
Т1 |
2 |
0 |
|
|
Т2 |
0 |
15 |
|
|
0 |
14 |
16 |
|
|
2 |
2 |
6 |
|
Т6= |
7 |
12 |
14 |
|
0 |
0 |
4 |
||
|
||||
|
Т3 |
7 |
9 |
|
|
Т4 |
0 |
4 |
|
|
0 |
17 |
19 |
|
|
5 |
5 |
9 |
|
|
10 |
19 |
19 |
|
Т7= |
0 |
0 |
4 |
|
|
Т5 |
7 |
9 |
|
|
Т4 |
0 |
4 |
|
Рассмотрим Т<19 (Т<17).
Из матрицы Т7 получаем Т4=7, Т5=0, следовательно, зависимость (5;7) не учитывается.
Из матрицы Т6 получаем Т4=7, Т3=7, следовательно, зависимость (3;6) учитывается. Из матрицы Т4 получаем Т2=2, Т1=3, следовательно, зависимости (1;4) и (2;4) учи-
тываются.
Таким образом, получим решение, в котором зависимость (5;7) не учитывается, а зависимости (3;6), (1;4) и (2;4)-учитываются. Продолжительность проекта составляет Т=17, а дополнительные затраты равны 5. Продолжительность работ увеличилась в сумме на 7 единиц.
Таким образом, рассмотрен метод решения задач дискретной оптимизации – метод дихотомического программирования. Идея метода заключается в возможности представления функции в виде суперпозиции более простых функций.
91
Метод дихотомического программирования применён для решения следующих задач управления проектами:
−задачи построения календарного плана с минимальной продолжительностью проекта;
−задачи построения календарного плана с минимальными дополнительными затратами;
−задачи построения календарного плана заданной продолжительности при минимальном увеличении затрат.
Задача оптимизации последовательности выполнения проектов заключается в том, чтобы выбрать наиболее оптимальную очерёдность выполнения работ. Так, например, если результаты одного проекта i можно использовать в другом проекте j, что сократит его продолжительность или стоимость, то, естественно, проект i предпочтительно завершить до начала проекта j.
Суть задачи построения календарного плана с минимальными дополнительными затратами состоит в том, чтобы максимально сократить рост затрат на реализацию проекта.
Библиографический список
1.Алферов, В.И. Основы научных исследований по управлению строительным производством: лабораторный практикум / В.И., Алферов, С.А. Баркалов. П.Н. Курочка, Т.В. Мещерякова, В.Л. Порядина. - Воронеж: "Научная книга", 2011. - 188 с.
2.Баркалов, С.А. Математические методы и модели в управлении и их реализация в MS EXEL: учеб. пособие / С.А. Баркалов, С.И. Моисеев, В.Л. Порядина / Воронежский ГАСУ. - Воронеж. 2015. - 264 с.
3.Дихотомическое представление задачи о ранце / И.В. Бурков., А.А. Волков, В.Л. Порядина В сборнике: Современные проблемы горно-металлургического комплекса. Наука и производство. Материалы Двенадцатой Всероссийской научно-практической конференции, с международным участием. 2015. С. 130.
4.Метод оптимизации грузопотока, основанный на положениях теории графов / С.А. Баркалов, В.Л. Порядина, М.В. Толкач . Современные проблемы горно-металлургического комплекса. Наука и производство. Материалы Двенадцатой Всероссийской научно-практической конференции, с международным участием. 2015. С. 44.
5.Модели формирования расписаний для специальных систем планирования / Т.В. Азарнова, В.Л. Порядина, А.Л. Ухин. Вестник Воронежского института экономики и социального управления. 2015. № 4. С. 3-10.
6.Оптимизация объемов работ в управлении проектами / С.А. Баркалов, В.Л. Порядина, Д.Н. Золоторев. Экономика и менеджмент систем управления. 2014. Т. 12, № 2. С. 11-20.
7.В.Л. Порядина Управление социально-экономическими проектами: конкурсный подход: монография. – Воронеж: Издательско-полиграфический центр "Научная книга", 2015. – 230 с.
8.В.Л. Порядина, Основы научных исследований в управлении социальноэкономическими системами / В.Л. Порядина, С.А. Баркалов, Т.Г. Лихачева. Воронежский ГАСУ.
—Воронеж, 2015. — 262 с.
9.Формирование календарного плана взаимозависимых проектов / И.В. Буркова, В.Л. Порядина, Г.В. Звенищева . Экономика и менеджмент систем управления. 2014 Т. 14. № 4.1. С. 139-149
10.MODEL OF COMPETITIVE MANAGEMENT OF REGIONAL BUILDING PROJECTS / Barkalov S.A., Poryadina V.L. Вестник Южно-Уральского государственного университета. Серия: Компьютерные технологии, управление, радиоэлектроника. 2016. Т. 16. № 2. С. 131-136.
92
