2945

УДК 519.8

Воронежский государственный архитектурно-строительный университет Доцент кафедры «Управления строительством» С.Н. Уксусов Российский экономический университет им. Г. В. Плеханова Студентка И.А. Минакова Россия, г.Воронеж, тел.:8-905-02-00-240

С.Н.Уксусов, И.А. Минакова

Логистическая задача управления производством энергоемкой продукции

Рассмотрена модель логистической задачи управления производством энергоемкой продукции, позволяющая обеспечить наилучшее сочетание прибыли и рентабельности производства. Разработан метод решения данной задачи методом жордановых исключений.

S.N.Uksusov, I.A. Minakova

Logistical challenge the production of energy-intensive production management

The model of logistics management tasks of production of energyintensive products, which allows to provide the best combination of profit and profitability. A method for solving this problem by Jordan exceptions.

Введение

В настоящее время созданы такие системы учета электроэнергии (электронные счетчики), которые позволяют узнать расход электроэнергии с учетом динамики её потребления в течение суток. В связи с этим появилась возможность так спланировать производственный процесс, что наиболее энергоемкие виды продукции выпускались в то время, когда цена на электроэнергию являлась минимальной.

Данная задача есть задача нахождения максимальной рентабельности производства по отношению к затратам на используемую электроэнергию. Для её описания разработана специальная модель задачи дробно-линейного программирования, которую можно решить методом жордановых исключений [1].

Однако получение максимальной рентабельности не гарантирует достижение предприятием максимальной прибыли. Ниже предлагается модель логистической задачи, в которой сочетаются критерии нахождения максимальной прибыли и наибольшей рентабельности предприятия.

Постановка задачи и построение модели

Предположим, что некоторое предприятие, работая круглосуточно, производит энергоемкую продукцию n видов. Для производства единицы продукции j-го вида требуется разное количество электроэнергии. Тарифы на электроэнергию зависят от времени

суток. Обозначим их через:

d1 (р/кВтч) - тариф во время пиковой нагрузки (с 700 до 1000 и с 1700 до 2100); d2 (р/кВтч) - тариф во время дневной полупиковой нагрузки (с 1000 до 1700 ); d3 (р/кВтч) - тариф во время вечерней полупиковой нагрузки (с 2100 до 2300 ); d4 (р/кВтч) - тариф во время ночной нагрузки (с 2300 до 700 ).

Продукция одного и того же вида, выпущенная в разное время суток, имеет разную себестоимость. Для того чтобы различить продукцию, выпущенную в разное время суток,

© Уксусов С.Н., Минакова И.А., 2016

123

Обратим внимание на то, что функция p(X ) совпадает с целевой функцией

В свою очередь, после выхода в область планов, когда в результате нескольких пересчетов методом жордановых исключений правый столбец (столбец свободных членов) будет состоять только из неотрицательных элементов, мы приходим к табл. 3:

Таблица 3

Табл. 3 получена из табл. 2 в результате нескольких шагов метода жордановых исключений. После пересчетов некоторые свободные переменные xj меняются на базис-

ные yi . Новые коэффициенты табл. 3 обозначены αij , правые части βi ≥ 0 , Q( X0 ) ≠ 0. Последнее неравенство достигается за счет того, что система (2) содержит ограничения вида xkj ≥ bkj .

На этапе выхода в область планов алгоритм решения задач линейного и дробнолинейного программирования совпадают. В результате из табл. 3 мы находим первона-

126

следующим формулам:

∆1j = ∆2j Q(X0 )− hj P(X0 ) .

Таким образом, получив табл. 3, мы нашли первоначальный опорный план и проверили его на оптимальность относительно сразу двух задач (максимальной прибыли и максимальной рентабельности).

2. Построение модели логистической задачи.

Составим следующую модель логистической задачи, в которой сочетаются критерии нахождения максимальной прибыли и наибольшей рентабельности предприятия. Так

как одновременная максимизация целевых функций f1 (X ) и f2 (X ) , как правило, невозможна, то в качестве критерия оценки найденного опорного плана будем использовать

ность, то α ближе к единице. Добавим к табл. 3 строку, содержащую оценки ∆ j . Получим табл. 4.

127

Таблица 4

Для нахождения оптимальности опорного плана логистической задачи будем добиваться неотрицательности оценок ∆ j . В результате нескольких шагов метода жордано-

вых исключений мы получим план, на котором достигается оптимальное сочетание прибыли предприятия с рентабельностью.

Библиографический список

1.Уксусов, С.Н. Решение задачи планирования производства с переменными ресурсами методом жордановых исключений / С.Н. Уксусов, С.А. Баркалов, Г.В. Зенищева // «Управление современными сложными системами»: Сборник трудов международной конференции. – Воронеж, 2013. - с. 210-220.

2.С.Н. Уксусов. Решение задачи планирования производства с учетом хранения произведенной продукции методом жордановых исключений / С.Н. Уксусов, С.В. Егорочев // «Управление современными сложными системами»: Сборник трудов международной конференции – Воронеж, 2013. - с.198-210.

3.Уксусов, С.Н. Решение задачи динамического управления производством методом жордановых исключений / С.Н. Уксусов, А.В. Соловьев// Современные сложные системы управления : материалы международной научно-практической конференции, Воронеж, 8-10 июля 2014 г. : в 2 ч.

–Воронеж, 2014. – Ч. 2. – С. 124-129.

4.Метод Штифеля и его применение в линейной алгебре и математическом программировании : Учеб.-метод. пособие по спец. "Математика" 010100 для студентов 3-4 курсов мат. фак. Воронеж : ЛОП ВГУ, 2003. – 73 с. (http://window.edu.ru/resource/013/27013)

5.Уксусов, С.Н. Метод Штифеля в линейном программировании // Стратегии развития – инновационно-инвестиционную активность : материалы регион. межвуз. науч.-прак. конф. (Воронеж, 15-18 апр. 2008 г.). – Воронеж, 2008. – Ч. II. – С. 19-24.

6.Уксусов, С.Н. Задача определения рентабельности затрат на производство при условии хранения готовой продукции / А.В. Соловьев, С.Н. Уксусов // Экономика и менеджмент систем управления. – Воронеж, 2014. – № 1.3 (11). - С. 407-416.

7.Уксусов, С.Н. Математическая модель рентабельности затрат на производство продукции при условии ее хранения / С.Н. Уксусов, А.В. Соловьев // Научный вестник Воронежского государственного архитектурно-строительного университета. Сер. Управление строительством. – Воронеж, 2014. – Вып. 1(6). – С. 133-142.

128

УДК 658.1-50

Воронежский государственный архитектурно-строительный университет к. техн. н., доц. каф. "Управление строительством" В.Л. Порядина Россия, г. Воронеж, тел.: 276-40-07

В.Л. Порядина

КОМПЛЕКСНОЕ ОЦЕНИВАНИЕ РЕЗУЛЬТАТОВ ДЕЯТЕЛЬНОСТИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОЙ СИСТЕМЫ

НА ОСНОВЕ ОБОБЩЕННЫХ АДДИТИВНЫХ СВЕРТОК

В данной статье разрабатывается процедура комплексного оценивания; описывается ряд специфических требований к механизму оценки, учет которых существенно влияет на результаты функционирования системы в целом и ее элементов. Рассматривается проблема выбора правил агрегирования (свертки) локальных оценок в комплексную, а также связанная с этим проблема замены одного вида свертки другим. Описанная в работе модель позволяет решить задачу оптимального приближенного представления матричной свертки в виде обобщенной аддитивной свертки.

V.L. Poryadina

COMPREHENSIVE EVALUATION OF THE OUTCOME OF THE SOCIO-ECONOMIC SYSTEM

BASED GENERALIZED ADDITIVE CONVOLUTIONS

In this paper, we develop an integrated assessment procedure; describes a number of specific requirements to the mechanism of evaluation, taking into account that a significant effect on the results of operation of the system as a whole and its parts. The problem of the choice of aggregation rules (convolution) local estimates the complex, as well as the related problem of the replacement of one species by another convolution. Described in the model allows us to solve the problem of optimal approximate representation of the convolution matrix in the form of a generalized additive convolution.

При управлении социально-экономическими системами на различных этапах подготовки и принятия решений, связанных с разработкой планов, организацией стимулирования, распределением ресурсов и т.д., возникает задача выбора альтернатив, сравнение объектов. Основой для ее решения является сравнительная оценка вариантов (объектов).

В связи с тем, что объекты (варианты), как правило, характеризуются выбором параметров и имеют многоцелевое назначение, принятие решений осуществляется на основе результатов комплексного оценивания объектов (вариантов).

Методы комплексного оценивания многомерных объектов исследуются в теории принятия решений, теории иерархических систем, теории выбора, теории активных систем. При этом используются как традиционные подходы (квалиметрия, оптимизационные методы, многомерный статистический анализ), так и активно развивающиеся в настоящее время человеко-машинные процедуры как основа систем поддержки принятия решений.

При разработке методов комплексного оценивания и построения процедур оценки необходимо учитывать специфику конкретного объекта оценки. Объектом комплексного оценивания может быть научно-технический уровень изделия, проект сложной технической системы, социально-экономическая эффективность принимаемых управленческих решений и т.д.

© Порядина В.Л., 2016

129

Особое место занимают задачи комплексного оценивания результатов деятельности (производственных коллективов, научных коллективов, отдельных работников). Специфика этого типа задач определяется сложностью описания оцениваемых объектов и их активностью.

Сложность описания объекта определяется наличием набора разнородных показателей, характеризующих различные аспекты его деятельности и имеющих различную относительную важность (значимость), которая может меняться в различные периоды функционирования.

Активность объекта управления связана с наличием в составе объекта людей, которые могут иметь интересы, отличные от целей системы, что влияет на результаты деятельности, достоверность сообщаемой информации.

При разработке процедур комплексного оценивания необходимо как можно полнее учесть указанные особенности объекта оценки.

Анализ результатов теоретических исследований по проблемам комплексного оценивания, а также используемых на практике процедур оценки результатов деятельности, в том числе многочисленных конкурсных систем и систем премирования, показывает, что при их разработке мало внимания уделяется ряду специфических требований к механизму оценки. Эти требования вытесняют из особенностей организационной системы и оцениваемых элементов, и их учет в механизме комплексной оценки может существенно влиять на результаты функционирования системы в целом и ее элементов. К таким требованиям относятся:

1)учет различной (с точки зрения конечных целей системы) важности и значимости показателей, используемых для оценки;

2)обеспечение сопоставимости оцениваемых элементов посредством учета в механизме оценки неравенства условий их функционирования;

3)учет взаимопомощи элементов.

Одной из важных и мало исследованных проблем при разработке процедур комплексного оценивания является проблема выбора правил агрегирования (свертки) локальных оценок в комплексную, а также связанная с этим проблема замены одного вида свертки другим.

Для формирования обобщенной оценки используют следующие варианты процедур

агрегирования. Пусть {Kl }, l = 1,l0 — множество критериев, на основе которых фор-

мируется обобщенная оценка.

Если качественным свойством целей элементов является равномерное (в определённом соотношении) улучшение оценок по всем критериям, то соответствующая обобщенная оценка имеет вид

где γl - положительные параметры, отражающие информацию об относительной важно-

сти различных критериев.

Если качественным свойством целей является улучшение оценки хотя бы по одному критерию, то соответствующая обобщенная оценка имеет вид

Если цели, поставленные перед организацией, носят смешанный характер (и улучшение всех показателей, и достижение высоких результатов в каком-либо направлении), то применяется средневзвешенная степенная оценка деятельности:

130

l0

F(k) = [∑(kl 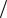γ l )s ]1/ s , s≠0.

l=1

При S=1 получаем простейший и весьма распространённый вид оценки (линейная свертка):

0

F(k) = ∑l kl .

l=1 γl

Если в этом выражении применить к локальным критериям нелинейные преобразования шкал, то получим аддитивную свертку; если в этом выражении применить преобразование шкалы и к комплексному критерию, то получим мультипликативную свертку

l0

F(k) = ∏kl1γ l .

l=1

Основание 1. Все представленные процедуры агрегирования предполагают веерную структуру критериев. На практике же часто критерии бывают взаимосвязаны и образуют сложную иерархическую структуру, которая может быть заменена наиболее простой бинарной структурой.

Достоинствам бинарной структуры является то, что она позволяет решать задачу комплексного оценивания по нескольким критериям путем многошаговой процедуры агрегирования, причем на каждом шаге производится агрегирование оценок только по двум критериям. А это упрощает задачу выбора правил агрегирования, поскольку соответствует реальным возможностям человека в выдаче непротиворечивой устойчивой информации (гипотеза бинарности). Эта гипотеза утверждает, что человек устойчиво сравнивает и разбивает на классы объекты, отличающиеся оценками по двум критериальным свойствам.

При попарном обобщении оценок, построенных на дискретных шкалах, то есть имеющих конечное число градаций, универсальной нормой представления сверток любого типа являются таблично заданные функции свертки - матрицы свертки.

Таким образом, матричные свертки являются универсальной формой представления свертки любого вида и дают широкие возможности для гибкого описания различных управленческих стратегий.

Встает вопрос о возможности приближения матричной свертки сверткой другого вида с минимальной ошибкой приближения. Для этой цели предлагается использовать обобщенную аддитивную свертку. Обобщенной аддитивной сверткой назовем аддитив-

ную свертку, к которой применено некоторое нелинейное преобразование ψ (•) . В

этом случае обобщенная оценка по двум локальным критериям равна ψ (ui + vj ). Рассмотрим случай, когда обобщённая оценка элемента определяется путем агре-

гирования локальных оценок по двум критериям – K1 и K 2 . Значения локальных оценок заданы на произвольных дискретных шкалах.

для i = 1, n , j = , m ;

3) в матрице отсутствуют одинаковые строки и одинаковые столбцы.

Задача поиска такого вида обобщенной аддитивной свертки, которая дает оптимальное приближение заданной матричной свертки может быть поставлена следующим образом:

Выбор критерия приближения в виде (1) определяется принципом максимального гарантированного результата в условиях неопределенности о конкретных значениях кри-

териев (конкретной паре оценок ( i , j ) ). Требование минимума ошибки для лю-

бой пары ( i , j ) и приводит к минимальному критерию.

Теорема. Необходимым и достаточным условием точного представления положи-

Таким образом, согласно теореме задача точного представления матричной свертки в виде обобщенной аддитивной свертки может быть сведена к поиску решения системы линейных неравенств (2).

Схема решения задачи точного представления матрицы С в виде обобщенной аддитивной свертки состоит из 3-х этапов:

1 этап – формирование неравенств для данной матрицы С;

2этап – решение системы неравенств, определение (u; v) ;

3этап – построение неубывающей функции ψ (ω) такой, что ψ (ui* + v*j ) = cij .

Заданная в таком виде функция ψ (•) является неубывающей и точно восстанав-

ливает исходную матрицу С.

Таким образом, основной проблемой решения задачи точного представления является реализация 2 этапа – решение системы неравенств (2).

Рассмотрим несколько подходов к решению (2), каждый из которых состоит в сведении (2) к некоторой стандартной задаче, для которой существуют эффективные методы решения.

Первый подход – сведение (2) к основной задаче линейного программирования. Для этого вводится критерий оптимальности

и от неравенств (2) переходят к системе нестрогих неравенств:

ui − ui−1 ≥ θ , v j − v j−1 ≥ θ , i = ,n, j = 2,m,

(ui + v j ) − (uk + vs ) ≥ θ , [(i, j), (k, s)] L′′ ,

132