Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2945

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.66 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

шений. В этом случае Р называется векторным нечётким отношением предпочтения (ВНОП). Первое, что надо сделать для этого случая, это определить соответствующее множество Парето. Формула (3) не может быть использована для этой цели. Вспомним, что каждому

Pj , j =1,m соответствует согласованное с ним чёткое отношение предпочтения Fj в соот-

ветствии с формулой (4).

Таким образом, вектор Р с нечёткими компонентами следует перевести в вектор F = {F1, F2 ,..., Fm } с чёткими компонентами. Для последнего определяется отношение Па-

рето-доминирования FP = I Fj и множество Парето XП (FP ) традиционным путём, как это

j=1

принято в многокритериальных задачах интерпретации результатов натурного эксперимента. Обозначим через X PUND множество чётко недоминируемых решений по всему вектору Р, т.е. по всем его компонентам:

X UND = X	П	(F ).	(5)
P	П	P

Очевидно, что если вектор Р содержит одну компоненту, то X PUND совпадает с XPUND (µ). Таким образом, множество X PUND выполняет роль множества Парето в нечётких

многокритериальных задачах интерпретации результатов натурного эксперимента: оно является им по своей сущности. Это означает, что имеется возможность оценивать на эффективность любые правила, алгоритмы и процедуры выбора [2]. Они эффективны тогда и только

тогда, когда предлагаемое ими решение находится в X PUND .

Утверждение 4. Если все компоненты вектора Р транзитивны, а Х конечно, то X PUND (µ)≠ 0/ и внешне устойчиво.

Доказательство утверждения 4. Если все Pj , j = 1,m транзитивны, то и соответствующие им Fj транзитивны. Отсюда следует транзитивность FP . Поскольку Х конечно, то множество Парето X П (FP )≠ 0/ и внешне устойчиво. То же можно утверждать и относительно X PUND . Утверждение доказано.

Эффективные свёртки векторных нечётких отношений предпочтения

В общем случае X PUND может не устраивать ЛПР, поскольку оно может содержать

большое количество решений. В этом случае для уменьшения множества, из которого следует выбирать решение, используют дополнительную информацию или некоторые логические допущения, а чаще и то и другое вместе. Одним из таких путей является введение свёрток вектора Р, т.е. замена ВНОП одним НОП по определённому правилу.

Некоторое НОП Р назовём свёрткой вектора Р, если его функция принадлежности

есть µ(x, y) = f [µ1 (x, y), µ2 (x, y),..., µm (x, y)].

На основании введённой свёртки выбор наилучших решений осуществляется затем в соответствии с формулой (3), приведём примеры свёрток:

		V	(x, y) = min µ j (x, y);
µ		V	(x, y) = min µ j (x, y);	(6)
			j=1,m
		Z	(x, y) = min µ j (x, y);
µ		Z	(x, y) = min µ j (x, y);	(7)
			j=1,m
	L (x, y,λ)= ∑m λj µ j (x, y),
µ	L (x, y,λ)= ∑m λj µ j (x, y),			(8)
			j=1
			153

где λ = {λ ,λ ...,λ },λ Λ,Λ = λ			λ		≥ 0,∑λ =1 .
					m
1 ,	m			j		j
					j=1

Свёртку Р назовём эффективной, если X UND (							µ	) X UND .
								P
Утверждение 5. Линейная свёртка ВНОП, представленная формулой (8), эффективна
для любых λ Λ .							(x, y) F S . Это означает, что все
Доказательство		утверждения			5. Пусть		(x, y) F S . Это означает, что все
								P

∆ j (x, y)≥ 0 и хотя бы для одного j выполняется строгое неравенство. Отсюда следует, что

∆

(x, y)> 0, что даёт (x, y) F S , где

∑λ

F на основе формулы (4) согласовано с ли-

j=1

нейной свёрткой, представленной формулой (8), следовательно, F S

F S , откуда сразу по-

лучается X

(F ) X

(F ), т.е. X UND (µ

)

X UND . Утверждение доказано.

Утверждение 6. Свёртка ВНОП, представленная формулой (6), эффективна, если

µi (x, y)+ µ j (y, x) = 1 для всех

j =

1, m

Доказательство утверждения 6. Пусть x X UND (

). Это означает, что в Х не суще-

ствует y такого, что (y, x) F S , где F = {(x, y)

(x, y)− µ

(y, x)≥ 0}. Другими слова-

ми, для всех y X имеет место неравенство: min µ j (y, x)≤ min µ j (x, y).

j=1,m

Пусть

для

фиксированного

y X

min µ j (y, x)− µ j0 (y, x).

Тогда

j=1,m

µ j (x, y) = max µ j (x, y). Так

как µ j

(y, x)≤ min µ j

(x, y)≤ µ j

(x, y),

то ∆ j (y, x)≤ 0.

=1,m

j=1,m

Причём при ∆ j (y, x)= 0 имеем: µ j (x, y)= µ j (y, x)=1/ 2 для любого

j =

1, m

, т.е. эле-

менты x и y равноценны. Таким образом, для каждого

y X

получаем: либо (x, y) Fl ,

∆ j (y, x) = 0 для

т.е.

любого

j =

1, m

либо хотя

бы при одном

j, а именно, при

j = j0∆ j (y, x)< 0 . Следовательно, в Х не найдётся элемента y такого, что все ∆ j (y, x)≥ 0 и хотя бы для одного j ∆ j (y, x) > 0. А это и означает, что x X П (FP ). Утверждение дока-

зано.

В многокритериальных задачах интерпретации результатов натурного эксперимента известен результат о достижимости любого решения из множества Парето варьированием

значений коэффициентов важности λj в линейной свёртке [3].

Аналогичный результат может быть доказан для линейной свёртки ВНОП. Утверждение 7 (лемма Карлина для ВНОП). Пусть имеется ВНП Р. Тогда для произ-

вольного решения x0 X LUND (λ0 ), где X LUND (λ) = X UND (µ L ).

Доказательство	утверждения	7.	Пусть	x	0	X UND .	По	определению:
					0	P

∆(y, x0 )= {∆1 (y, x0 ), ∆2 (y, x0 ),...,∆m (y, x0 )}, y X , образует некоторое конечное множество точек в m-мерном пространстве и не имеет общих внутренних точек с положительным ортантом m-мерного пространства. Выпуклая оболочка этого множества, являясь вы-

пуклой комбинацией точек ∆(у, x0 ), y X , также не будет иметь общих внутренних точек

с положительным ортантом. Тогда на основе теоремы о разделяющей плоскости для двух выпуклых множеств, не имеющих общих внутренних точек, можно утверждать, что существует такой вектор, каждая компонента которого неотрицательна и хотя бы одна положитель-

154

m		(y, x0 )≤ 0. Компоненты aj
на, что имеет место неравенство: ∑aj	∆ j	(y, x0 )≤ 0. Компоненты aj		можно нормировать:
j=1
m				m	∆(y, x0 )≤ 0 .
λ0j = aj / ∑aj . Тогда вышеприведённое неравенство запишется в виде ∑λ0j					∆(y, x0 )≤ 0 .
j=1				j=1
Оно выполняется для всех y X , а это как раз и есть условие, что x			0	X UND (λ ) . Утвер-
			0	L	0
ждение доказано.

Взаимосвязь многокритериального и нечёткого представлений задачи интерпретации результатов натурного эксперимента

Этому вопросу мы придаём большое значение. Интуитивно ясно, что нечёткое представление задачи принятия решений должно быть шире чёткого многокритериального представления и включать его в себя. Точно так же, как понятие нечёткого множества включает в себя понятие обыкновенного чёткого множества, которое является его частным случаем. Этот факт отражён в следующем определении.

Будем говорить, что два представления задачи принятия решений: многокритериальное и нечёткое, согласованы (совместимы, непротиворечивы), если имеет место RKS FPS .

Сделаем одно уточнение к этому определению. В обоих случаях в нём понимается одна и та же задача принятия решений, что просто означает: оба представления заданы на одном и том же множестве конкурсных решений Х. из этого определения непосредственно следует, что

для согласованных представлений задачи принятия решений имеет место XPUND X ПK [4].

Заключение

Случай согласованных представлений интересен тем, что позволяет на основе введения векторного нечёткого отношения предпочтения уменьшить множество Парето для многокритериального представления задачи интерпретации результатов натурного эксперимента. При этом необязательно, чтобы число частных критериев эффективности совпадало с числом нечётких отношений предпочтения в наборе Р.

Библиографический список

1.Белоусов, В.Е. Анализ состояний сложных систем организационного управления с использованием решающих правил / В.Е. Белоусов, Хонг Тронг Тоан // Системы управления и информационные технологии. – 2012. – №2.2(48). – С. 237-239.

2.Борисов, А.Н. Обработка нечеткой информации в системах принятия решений / А.Н. Борисов, А.В. Алексеев, Г.В. Меркурьева. – М.: Радио и связь, 1989.

3.Белоусов, В.Е. К проблеме решения задач многокритериальной оптимизации / В.Е. Белоусов, А.В. Гайдук, В.Н. Золоторев // Системы управления и информационные технологии. – 2006. - № 3(25). – С.34-43.

4.Баркалов С.А. Методы и модели оценки эффективности бизнес-процессов / В.Е. Белоусов, С.А. Баркалов, Н.В. Санина: учебник ООО Издательство Научная книга, Воронеж, 2013.- 415 с.

155

УДК 004.855.3

Воронежский государственный архитектурно-строительный университет д. техн.. н., проф. каф. «Управление строительством» Ю.В. Бондаренко асп. каф. «Управление строительством» Кау Россия, г. Воронеж, тел.: 2-76-40-07

Ю.В. Бондаренко, Кау

МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА ОПРЕДЕЛНИЯ ПАРАМЕТРОВ НАТУРНО-ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА

ПРИ ИССЛЕДОВАНИИ СЛОЖНЫХ АГЕНТНЫХ СИСТЕМ

Рассматривается решение задач получения размерного ряда многопродуктовых производственных мощностей при использовании перспективных технологий строительства. Разработка таких рядов становится одной из центральных задач перспективного планирования специализации и концентрации строительного производства. В статье речь идет об определении не одного, так или иначе фиксированного, а нескольких значений производственной мощности, упорядоченных тем или иным способом.

Y.V.Bondarenko, Kau

MULTI-OBJECTIVE PARAMETER DEFINITIONS-NATURAL TASK OF COMPUTING EXPERIMENT IN THE STUDY OF COMPLEX AGENT SYSTEMS

In this paper we consider the problem of obtaining the size of a number of multi-product manufacturing facilities using advanced technologies of construction. The development of such series has become one of the central tasks of long-term planning of the construction of specialization and concentration of production. The article deals with the definition of more than one way or another fixed, and several values of production capacity, ordered one way or another.

Под размерным рядом производственных мощностей в строительстве понимается последовательность таких значений возможных объемов работ, при каждом из которых обеспечивается полная загрузка, по крайней мере, одного из входящих в соответствующий комплект видов оборудования и бригад, т.е. данный объем является для этого комплекта максимальным. Указанные виды оборудования образуют «узкие» звенья комплекта; их «расшивка» путем добавления единицы соответствующего оборудования обеспечивает переход к следующему комплекту с большей максимально возможной производительностью, т. е. повышение уровня производственной мощности. Для каждого такого комплекта оборудования

иопределяемого им уровня мощности могут быть рассчитаны различные показатели производства — объемные (парк оборудования, размер необходимой производственной площади, численность работающих и др.) и относительные, или удельные (производительность труда, квалиметрические показатели и т. п.). Существенно, что удельные показатели, отражающие эффективность строительного производства, хотя и имеют тенденцию к улучшению с ростом мощности, однако их зависимости от этого фактора не являются монотонными. При расчете размерных рядов мощностей следует ориентироваться на технологические процессы, подкрепленные перспективным оборудованием. Вместе с тем нужно учитывать реальные возможности получения и установки необходимого оборудования в данном периоде. При ограниченности такой возможности, а также принимая во внимание несовпадение условий производства, целесообразно предусматривать несколько вариантов технологических процессов

иразличные по составу наборы реализующего их строительного оборудования. Для каждого такого варианта рассчитывается свой размерный ряд. Эти ряды можно комбинировать, на-

156

пример, если возникает потребность в переходе, начиная с некоторого значения мощности, на более прогрессивный технологический процесс. Вместе с технологическим процессом выбираются, как известно, структура и организация строительного производства. Здесь также могут быть рассмотрены варианты, например поузловой и подетальной специализации, отличающиеся уровнем поставок по кооперации. Для каждого из них требуется свой размерный ряд.

Постановка задачи

Пусть в существующем или предлагаемом технологическом процессе строительного производства данной работы используется т видов основного оборудования. Единица оборудования вида i характеризуется годовым фондом времени работы Фi, станкоемкостью fi, выполнения технологической операции и другими показателями. Обозначим через xt искомое количество единиц оборудования i в произвольном комплекте x=(xt), а через y возможный объем работ [1]. На этом комплекте приходим к соотношениям, выражающим взаимосвязь данных величин:

fiy ≤ Фiхi , i= 1,…,m.	(1)
Очевидно, производство работ является функцией оборудования, т. е. у(х) на-
ходят как
0 ≤ у(х) ≤ (Фi/fi) i=1,...,m.	(2)
Из (2) следует, что максимально возможный при данном комплекте оборудова-
ния х= (хi) производство работ или производственную мощность у y(х) находят так:
yˆ(x)= min(Фi f i)xi	(3)
1≤i≤m	(3)

где Фi/fi=аi — годовая производительность единицы оборудования вида i.

Равенство (3) представляет собой формальную запись хорошо известного факта: максимальная мощность или производительность любого комплекта оборудования определяется производительностью наиболее «узкого» его звена (или звеньев — минимум aixi может достигаться и при нескольких значениях i). Ликвидируя проблемные звенья и добиваясь максимального использования создаваемых таким образом комплектов, получаем последовательность величин y(x), образующую, согласно данному определению, размерный ряд производственных мощностей {у (x)}. Таким образом, комплект оборудования x0= (хi0) и определяемую им мощность у(х0) являются оптимальными относительно выбранного показателя эффективности, если не существует комплекта с меньшим уровнем мощности, но с лучшим значением рассматриваемого критерия. В результате приходим к общей модели расчета разнородных мощностей оборудования при производстве строительно-монтажных работ.

Модель 1. Для каждого значения параметра b из отрезка 0≤b≤b` найти такой набор х=(хi) целых положительных чисел, на котором достигается наилучшее значение показателя эффективности производства F(x) при обязательном выполнении у(х) ≤ b и возможных ограничениях на размер потребляемых ресурсов dp(x), р=1,..., р', включая в их число степень загрузки отдельных групп или видов оборудования. Здесь у(х) находится по (3). Всякий оптимальный (в смысле данного выше определения) относительно F(x) комплект х=(хi) является также оптимальным по Парето относительно F(x) а затрат любых видов ресурсов dp(x), т. е. нельзя улучшить F(x), не увеличив эти затраты, и, наоборот, нельзя уменьшить затраты ни одного из этих ресурсов, не ухудшив F(x). Следовательно, множество решений нашей однопараметрической задачи (1) совпадает с множеством решений следующей многопараметрической задачи.

Модель 2. Найти такие наборы х=(хi) целых положительных чисел, на каждом из которых достигается наилучшее значение критериального показателя F(x) при условии у(х) ≤ b' и параметрических ограничениях dp(x) ≤ Dp, p=1,...,p', с параметрами Dp, пробегающими независимо лучи Dp ≤ 0.

Упорядочив решения любой из этих задач, т. е. расположив оптимальные комплекты х0— (хi°) в порядке возрастания у (хо) , получаем искомый размерный ряд оптимальных мощностей. Нетрудно доказать, что каждый следующий член последовательности превосходит

157

предыдущий не более чем в 2 раза. В случае необходимости увеличения числа членов ряда целесообразно наряду со скалярными использовать также и многоцелевые модели, например, следующую.

Модель 3. Для каждого значения параметра b из отрезка 0≤b≤b` найти все такие наборы x=(xi) целых положительных чисел, чтобы выполнялись ограничения модели 1 и каждый набор был оптимален по Парето относительно двух критериев: Fl(x) и F2(x).

С формальной точки зрения, полученные модели сводятся к задачам нелинейного параметрического целочисленного программирования, для решения которых нет общих методов. Однако содержательно их можно рассматривать как задачи поиска «приближенных наименьших кратных» ряда чисел аi i=1,..., т. Учитывая это, удалось найти простой и эффективный алгоритм, дающий полное и точное решение каждой из задач за конечное число ша-

гов, не превосходящее ∑b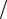ai , что существенно меньше, чем общее число всех возмож-

i=1

ных комплектов оборудования X=(Xi), приблизительно равное ∏b`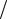ai [2,3].

i=1

Описанные модели являются достаточно общими. Раскрывая их критерии оптимальности и ограничения, можно получить семейство конкретных или рабочих моделей. Остановимся на некоторых из них.

Модель на максимум распределения ресурса [4]. В однопродуктовом случае при фиксированных технико-экономических показателях применяемого оборудования уровень отдачи прямо пропорционален степени его использования. Для характеристики последней введем средний коэффициент β (х) загрузки искомого комплекта х=(Xi), взвешенный по суммарной стоимости Ci входящего в него оборудования и занимаемых им производственных площадей:

β (x) = ∑ci xiαi (x)

i=1

m
∑ci xi .	(4)

i=1

Здесь через
αi (x)= yˆ (x) ai xi	(5)

обозначен коэффициент загрузки оборудования вида i (индивидуальный коэффициент загрузки). Очевидно, значения ai(x) и β (x)находятся между нулем и единицей. В принятых обозначениях показатель фондоотдачи γ (х) рассчитывается по формуле

γ (x)= ey(x) c (x)		(6)
		(6)
m
где е — стоимость единицы продукции, а с(х) = ∑ci xi — общая стоимость фондов.
i=1
Из (4) с учетом (5) и (6) следует:
β (x)= γ (x)∑m	ci eai ,	(7)
i=1
m
где ∑ci eai — константа, не зависящая от выбираемого комплекта x=(xi) и определяемой
i=1
им мощности у (x). Обозначив эту константу через: 1 γ max (x) и записав (7) в виде
γ (x)= β (x) max (x),
γ

видим, что γ max (x) — максимально возможное при заданных условиях значение фондоотда-

чи γ (х), которое достигается при уровне мощности, обеспечивающим полное использование всех видов оборудования. Указанный уровень мощности (обозначим его через у (х00)) — наименьшее общее кратное производительности всех видов оборудования, т.е. чисел аi. Как правило, этот показатель значительно превышает уровень потребности в рассматриваемой

158

продукции и представляет поэтому лишь теоретический интерес. Наоборот, γ max (x) являет-

ся важнейшей характеристикой принятой технологии, позволяющей, в частности, судить об ее предельной экономической эффективности.

Используя γ (x) в качестве критерия оптимальности модели (1), а также конкретизи-

руя систему ее условий, например, вводя ограничения на допустимые уровни загрузки отдельных групп или видов оборудования, получим модель на максимум фондоотдачи.

Для получения размерного ряда многопродуктовых производственных мощностей применяется освоенная практикой текущего отраслевого планирования модель расчета оптимальной мощности промышленного предприятия: оптимизировать

	n
Ф(z) = ∑ej zj			(8)
	j=1
при условиях
n	≤ϕi ,
∑aij zj	≤ϕi ,	i=l,..., т,	(9)
j=1
bj`≤zj≤bj`` ,		j = 1,..., т,	(10)

где aij — станкоемкость выполнения работы j бригадой i; zi — искомый объем выполнения работ вида j; bj`; bj`` — нижняя и верхняя границы возможного объема строительного производства работы j бригадой; еj — показатель критерия оптимальности по работе j, например производительность труда; фi — общий фонд времени работы строительно-монтажного оборудования вида i.

Модель (8) —(10) отражает возможности наличного парка основного технологического оборудования и фиксированного фонда времени его работы; с ее помощью определяется производственная мощность, наилучшим образом соответствующая этому парку машин и его возможностям. Будучи приемлемой для текущего календарного планирования, т. е. задач наилучшего использования уже созданного производственного аппарата, такая модель оказывается совершенно непригодной для перспективного планирования, основная цель которого — выявление наилучших направлений формирования этого аппарата, включая выбор состава и структуры парка оборудования, производственных площадей и других ресурсов. В указанной постановке задачи оптимизации перспективного календарного планирования велики неопределенность и неоднозначность величин фi.

Для адекватного описания этого обстоятельства необходимо модифицировать модель

(8) —(10): оптимизировать

	Ф(z, х)	(11)
при условиях
n
∑aij zj	≤ f i xi , i=l,..., т,	(12)
j=1
bj`≤ zj ≤bj0 , j = 1,..., n,		(13)
где xi — целые неотрицательные числа.

Здесь xi - уже не жестко фиксированные величины, а управляемые параметры, определяющие количество единиц устанавливаемого оборудования, а Ф(z, х) — в общем случае нелинейная функция от z=(zj) и х=( xi).

Решая задачу (12) —(14) при различных xi, найдем серию оптимальных планов, каждый из которых может рассматриваться как некоторая ступень многопродуктовой мощности, определяемая комплектом оборудования x=(xi). Упорядочив мощности по суммарному зна-

n	n
чению их натуральной z = ∑zj либо приведенной	z'= ∑ej zj , величины (еj — коэффици-
j=1	j=1
159

енты приведения), получим размерный ряд мпогопродуктовых мощностей. Выбирая теперь из него только те значения, которые монотонно улучшают принятый критерий Ф(z, х), построим размерный ряд оптимальных многопродуктовых мощностей.

Легко показать, что такая многопродуктовая модель является обобщением описанных выше однопродуктовых. Действительно, при n =1 ограничения (12) принимают вид aiz ≤ fixi , i =1, . . . , т. Отсюда z ≤ (fi/аi)xi . Обозначая теперь через z максимально возможный выпуск

продукции, т. е. производственную мощность, приходим к выражению z = min(f i ai)xi ,

1≤i≤m

совершенно аналогичному (3).

Введенную модель следует рассматривать в качестве базовой: раскрывая содержание критерия оптимальности Ф(z, х), на ее основе, как и в однопродуктовом случае, можно построить семейство конкретных или рабочих моделей. При каждом фиксированном наборе параметров х=( xi) (12) —(13) превращается в достаточно простую задачу линейного или нелинейного программирования, чем предопределяется и возможный метод решения.

Действительно, пусть известен начальный комплект оборудования х0 = (хi°) (при необходимости в качестве начального можно взять х с xi =1 при всех i). Знание xi позволяет фиксировать правые части (12) и в большинстве случаев линеаризовать целевую функцию,

n	m
например показатель фондоотдачи: F(z,x) = ∑ej zj	/ ∑d j xj , где di, — стоимость единицы
j=1	j=1

оборудования вида i.

На оптимальном решении полученной линейной задачи некоторые ограничения (12) обратятся в равенства и зафиксируют образование «узких мест», препятствующих дальнейшему росту мощности. Для их ликвидации следует увеличить количество единиц оборудования соответствующих видов, т. е. перейти к следующему комплекту х`=(xi `), например, по правилу

			x	0	,
x`i			i
x`i	=		0	+1,
	x		0	+1,
		i

n	0		0 ,
если ∑aij zj		≤ fi xi
j=1				(14)
n
		0 = fi xi		0 ,
если ∑aij zj

j=1

где z°=(zj°) —оптимальное решение задачи при (хi) — (хi°). С учетом новых значений параметров xi правые части ограничений (12) пересчитываются и вся процедура решения повторяется до достижения всеми переменными zj их верхних границ.

Правило (14) перехода к новому комплекту не является единственно возможным. Например, для обеспечения дальнейшего движения совсем не обязательно «расшивать» сразу все «узкие места» — достаточно «расшить» хотя бы одно из них. Можно оптимизировать выбор «расшиваемого узкого места», если включить в модель (11) —(14) дополнительное

ограничение Х = ∑xi , в котором управляемый параметр X имеет смысл общего количе-

i=1

ства единиц оборудования в каждом данном комплекте. Теперь достаточно изменять на каждом шаге q лишь один этот параметр, вводя дополнительные условия xiq ≥ xiq-1 , где xiq — количество единиц оборудования вида i на шаге q.

Для рассматриваемого алгоритма, так же как и в однопродуктовом случае, легко указать верхнюю оценку общего числа итераций Q, необходимых для полного решения задачи:

m		n	″		− X	0
Q ≤ ∑−	−∑aij b j		″	f i	− X
i=1		j=1

где [z] — целая часть z; Х0 — количество единиц оборудования в начальном комплекте.

Заключение

Размерные ряды оптимальных мощностей можно использовать для обоснования оптимальных размеров предприятий или цехов, для формирования вариантов возможного раз-

160

вития и специализации производственных объектов в задачах оптимального планирования строительного производства. На многих строительных предприятиях абсолютно нелимитирующие строительно-монтажные работы группы оборудования составляют 70-80 % общего количества групп взаимозаменяемого оборудования. Столь высокий процент свидетельствует о наличии больших резервов мощности, не вскрываемых расчетами по обычным моделям оптимизации

Библиографический список

2.Борисов, А.Н. Обработка нечеткой информации в системах принятия решений / А.В. Алексеев, Г.В. Меркурьева– М.: Радио и связь, 1989.

3.Белоусов, В.Е. К проблеме решения задач многокритериальной оптимизации / Белоусов В.Е., Гайдук А.В., Золоторев В.Н. // Системы управления и информационные технологии. – 2006. - № 3(25). – С.34-43.

4.Баркалов, С.А. Методы и модели оценки эффективности бизнес-процессов: учебник / С.А. Баркалов, В.Е. Белоусов, Н.В. Санина. – Воронеж: ООО Издательство. Научная книга, 2013.- 415 с.

161

УДК 669.046:658

Воронежский государственный архитектурно-строительный университет ст. преп. каф. «Автоматизация техн. процессов и производств» О.В. Царегородцева асп. каф. «Управление строительством» М. С. Доударан асп. каф. «Управление строительством» И.С.Скрипников Россия, г. Воронеж, тел.: 2-76-40-07

О.В. Царегородцева, Мейсам Сиэми Доударан, И.С. Скрипников

МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА ПРОЕКТИРОВАНИЯ СЛОЖНОЙ АКТИВНОЙ СИСТЕМЫ

Рассматривается модель анализа многокритериальной задачи, позволяющая существенно снизить проблемы, возникающие при проектировании сложных технических систем в случаях, когда требуется существенно снизить размерность векторного критерия в случае его избыточности, или показать, что такое сокращение невозможно

MULTI-OBJECTIVE TASK OF DESIGNING COMPLEX ACTIVE SYSTEMS

In this article the model of the analysis of a multicriteria task allowing to lower significantly the problems arising at design of difficult technical systems in cases when it is required to reduce significantly dimension of vector criterion in case of its redundancy or to show is considered that such reduction is impossible.

Введение

Многие задачи оптимального проектирования сложных технических систем имеют многокритериальную основу. Причем в качестве критериев как правило, берутся технические характеристики системы, а стратегии (альтернативы) представляют собой варианты ее проектов, задаваемые в виде наборов значений конструктивных параметров. Поскольку многокритериальные задачи проектирования сложных систем имеют большую размерность пространства стратегий и значительного времени расчёта характеристик их решение становится довольно затруднительным.

Другая особенность заключается в необходимости повторного решения многокритериальных задач с теми же критериями, но изменёнными множествами стратегий в связи с возможными в ходе проектирования изменениями конструктивных и функциональных ограничений, определяющих техническую систему [1,2].

Постановка задачи

В многокритериальных задачах «качество» (или «полезность», «ценность», «эффективность» и т. п.) объектов оценивается с помощью критериев K1, K2 ,..., Km (m ≥ 2). Под

критерием Ki понимается функция, отображающая множество объектов Q в некоторое, содержащее не менее двух точек, подмножество Xi числовой прямой Re. Это множество называют шкалой i-го критерия, а его элементы – шкальными оценками.

Критерии Ki образуют векторный критерий K = (K1,..., Km ) , отображающий множество Q во множество χ = X1 × X2 ×...× Xm векторов, компонентами которых являются шкальные оценки. В общем случае не для всякого вектора x из χ может существовать соответствующий объект a, т. е. такой, что K(a)= x . Однако для анализа задачи и получения необходимой информации с целью её решения удобно оперировать векторами из χ , кото-

162

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.64 Mб22938.pdf
#
15.11.20222.65 Mб12939.pdf
#
15.11.20222.65 Mб12940.pdf
#
15.11.20222.65 Mб32942.pdf
#
15.11.20222.66 Mб02943.pdf
#
15.11.20222.66 Mб12945.pdf
#
15.11.20222.67 Mб12947.pdf
#
15.11.20222.67 Mб02949.pdf
#
15.11.20222.67 Mб02950.pdf
#
15.11.20222.67 Mб32951.pdf
#
15.11.20222.67 Mб02952.pdf