
2788
.pdf
Разложим выражения для Rx( |
(k) + (k)) и Ry( |
(k) + |
(k)) в ряд вблизи точки (x, y), |
|||||||||||||||||||
ограничиваясь только линейными слагаемыми: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
R(k 1) (ξ(k ) |
Δξ(k ) ) R(k ) (ξ(k ) ) |
(k ) |
N j |
X |
|
|
(k ) |
|
N j |
X |
|
(k ) |
|
N j |
|
X |
|
|
, |
|||
1 |
|
|
j |
|
2 |
|
|
j |
3 |
|
|
|
j |
|||||||||
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
j |
1 |
|
|
|
|
j |
2 |
|
|
|
j |
3 |
|
|
|
|
|
|||
R(k 1) (ξ(k ) |
Δξ(k ) ) R(k ) (ξ(k ) ) |
(k ) |
N j |
Y |
|
(k ) |
|
N j |
Y |
|
(k ) |
|
N j |
Y |
|
|
. |
|||||
1 |
|
|
j |
2 |
|
j |
3 |
|
j |
|
||||||||||||
y |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
j |
1 |
|
|
|
j |
2 |
|
|
j |
3 |
|
|
|
|
|
|||||
Если учесть соотношение, связывающее i: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
3 = – |
1 – |
|
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то получим систему относительно |
(k ) |
и |
(k ) : |
|
1 |
|
2 |
x |
|
x |
(k ) |
x |
|
x |
(k ) |
R(k ) |
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
2 |
x |
1 |
3 |
|
2 |
3 |
|
|
||
y |
|
y |
(k ) |
y |
|
y |
(k ) |
R(k ) |
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
2 |
y |
1 |
3 |
|
2 |
3 |
|
|
||
,
,
где |
x |
|
N j |
X j , |
y |
|
N j |
Yj |
. Решив данную систему, например, ме- |
|
|
j |
|
|
j |
|
|||||
i |
i |
i |
i |
|||||||
|
|
|
|
тодом Крамера, получим искомые приращения  i(k ) .
i(k ) .
Поскольку в формулах, связывающих декартовы и локальные координаты, нелинейности определяются полиномами, т.е. монотонными функциями без особенностей, алгоритм метода Ньютона сходится за 2–3 итерации.
Однако в случае, когда используются симплексные конечные элементы (треугольники и тетраэдры) с прямыми сторонами, то зависимости (78) становятся линейными (афинное преобразование). Тогда локальные координаты выражаются с помощью прямых формул:
|
1 |
|
(a |
|
|
b x |
c |
y) , |
i = 1, 2, 3 – для треугольников, |
(79) |
|
i |
|
i |
|||||||||
2 A |
|
|
i |
i |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(a |
|
b x |
c y |
d |
z) , i = 1, 2, 3, 4 – для тетраэдров, |
(80) |
||
i |
|
|
i |
||||||||
6V |
|
|
|
i |
i |
|
i |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
где A, V – соответственно площадь и объем конечного элемента, коэффициенты {ai, bi, ci, di} выражаются через координаты вершин элемента. Естественно, вычисление локальных координат по формулам (79-80) предпочтительнее, чем с помощью итераций Ньютона, поэтому эффективность вычислений можно повысить, если изопараметрические (криволинейные) элементы использовать только вблизи физически значимых криволинейных границ и разделов сред, а внутреннюю область заполнять афинными (прямолинейными) элементами. Так как в рассматриваемой СКМ расчетная область задачи предварительно разбивается на зоны (суперэлементы), дискретизация которых производится последо-

52
вательно и независимо друг от друга, то в различных зонах оказывается возможным использовать элементы различных типов. Например, зоны, имеющие криволинейные границы, целесообразно разбивать на изопараметрические элементы, а в остальных использовать афинные элементы.
Блок интегральных характеристик обеспечивает вычисление таких ве-
личин, как запасенная энергия системы, сила и момент сил, действующие на некоторую помечаемую пользователем поверхность со стороны поля, индуктивность, максимальный градиент функции, и др. Интегральные величины могут быть двух типов. Первые вычисляются интегрированием по объему конечных элементов, а вторые – интегрированием по их границам. Следует отметить, что МКЭ естественным образом предназначен для их вычисления: требуется лишь организация цикла по элементам, интегрирование на каждом элементе и накопление результатов в соответствующей переменной (сумме).
Запасенная энергия непосредственно связана с функционалом задачи, который, как было сказано выше, минимизируется в МКЭ и определяется наиболее точно. Расчет производится по формуле:
|
|
|
|
W |
|
|
|
|
|
|
2 |
||
|
|
|
|
|
||
или |
W |
|
i |
j |
|
N |
|
|
|||||
|
2 |
|
|
|||
|
e |
|
e |
|||
|
|
|
|
|
||
2 dxdydz ,
(e) |
N (e) d |
|
|
S (e) , |
i |
j |
2 |
i j |
ij |
|
|
e |
|
где { Sij(e) } – матрица жесткости е-го конечного элемента.
Поскольку матрица жесткости в МКЭ вычисляется на этапе формирования системы уравнений, то вычисление энергии можно организовать эффективно, если сохранить в памяти компьютера матрицу жесткости. Кроме того, наиболее естественно расчет энергии осуществляется, если для решения СЛАУ применяется метод сопряженных градиентов. Данный метод решения систем вида Au = b основан непосредственно на минимизации функционала
F |
* |
1 |
u |
T |
Au bu , |
|
2 |
|
|||
|
|
|
|
|
величина которого совпадает с W с точностью до постоянного слагаемого. По значению F* можно контролировать процесс вычислений. Величина постоянной добавки определяется путем учета фиксированных узлов и может быть вычислена отдельно, либо на этапе формирования матрицы.
Сила, в отличие от энергии, определяется путем интегрирования по некоторой поверхности, а значит, по границам элементов, примыкающих к этой поверхности:
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
F |
|
|
dS , |
|
|
|
||
|
|
|
2 S |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(e) |
N (e) dS |
|
|
|
или |
F |
|
|
|
|
|
N |
n |
, |
||
|
|
|
i j |
|
|
||||||
|
2 |
|
|
|
i |
j |
e |
|
|||
|
e i, j |
Se |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|

53
где ne – нормаль к границе конечного элемента, в общем случае – для изопара-
метрических элементов – нормаль в пределах одного элемента меняется от точки к точке. Например, для изопараметрического тетраэдра вектор нормали определяется формулой
|
(bk |
, ck , dk ) |
|
, |
||
ne |
|
|
|
|
|
|
|
|
|
|
|
||
b2 |
c2 |
d 2 |
||||
|
|
k |
k |
k |
|
|
где bk, ck, dk – функции, зависящие от конкретных размеров элемента, его формы и положения в пространстве. Индекс k определяет номер локальной координате, которая равна 0 на Sе. В результате для компонент вектора силы в расчете на один конечный элемент получим выражения:
F (e)
x 2
F (e)
y 2
F (e)
z 2
i j Ni (u,v) N j (u,v)bk dudv ,
i, j S1
i j Ni (u,v) N j (u,v)ck dudv ,
i, j S1
i j Ni (u,v) N j (u,v)dk dudv .
i, j S1
Интегрирование проводится по области стандартного треугольного элемента 2 порядка с координатами узлов (0, 0), (0.5, 0), (1, 0), (0.5, 0.5), (0, 1), (0, 0.5). {Ni}
– функции формы этого элемента.
Блок построения графиков позволяет получать графики распределения функции u, ее производных и градиента вдоль любого заданного пользователем отрезка либо линии. Для двумерных областей, кроме этого, может быть построен график изменения нормальной производной u n вдоль граничной линии
n вдоль граничной линии
(прямой или кривой). Также для двумерных областей может быть построен трехмерный график, представляющий собой изображение поверхности u = u(x, y) с возможностью поворота относительно всех трех осей координат.
Рис. 23. Примеры построения графиков.

54
Значения функции, ее производных и градиента вычисляются блоком локальных характеристик в точках, расположенных вдоль выбранного контура с некоторым шагом. Затем по этим точкам строится график с использованием линейной аппроксимации, сплайнов либо метода наименьших квадратов. Помимо графического представления, вычисленные вдоль указанного контура данные могут быть выведены в форме таблицы на экран, принтер или в файл.
Блок визуализации поля содержит функции построения эквипотенциалей, матриц стрелок и цветовых карт. В трехмерном случае все они строятся на некоторой плоскости, пересекающей область. Уравнение плоскости может быть задано пользователем в виде Ax + By + Cz + D = 0, x = D, y = D или z = D.
Решение на всей области может быть записано в виде
u |
Ni(e)Ui , |
e |
i |
где Ni(e) – функция формы элемента e, связанная с узлом i. Построение эквипотенциалей с шагом требует решения уравнений
k Ni(e) (x, y, z)Ui , k = 0, 1, 2, ...
Ni(e) (x, y, z)Ui , k = 0, 1, 2, ...
i
на каждом элементе. В случае линейных треугольных элементов это не представляет большого труда, так как эквипотенциали в пределах одного элемента будут представлять собой отрезки прямых. Для квадратичных элементов они являются частями кривых, и необходимо вычислять несколько промежуточных точек внутри элемента.
Матрицы стрелок позволяют наглядно представить поведение градиента потенциальной функции во всей области или в ее части, определить районы наибольших и наименьших значений градиента. В заданной пользователем части области строится регулярная сетка узлов с заданным шагом, и в каждом из них вычисляется градиент, затем из каждого узла рисуется вектор, длина которого пропорциональна модулю градиента.
Рис. 24. Распределение эквипотенциалей внутри расчетной области.

55
Рис. 25. Матрица стрелок.
Функция построения цветовой карты позволяет определить районы наибольших и наименьших значений функции и ее градиента путем их окрашивания в разные цвета. В одном из режимов работы данной функции весь диапазон изменения выбранной величины делится на 10 поддиапазонов, и каждому из них ставится в соответствие свой цвет. Элементы, для которых значение этой величины попало в какой-либо поддиапазон, окрашиваются в соответствующий цвет. В другом режиме пользователь задает граничное значение величины, и окрашиваются только те элементы, для которых эта величина оказывается больше введенной пользователем.
Блок вывода результатов обеспечивает сохранение изображений и таблиц на диске в виде файлов либо вывод их на принтер для печати. В любой момент изображение, имеющееся на экране, может быть сохранено в виде BMPфайла (цветного или черно-белого), будь то изображение картины поля или график. Таблицы значений функции, градиента и т.д. могут быть сохранены в виде текстового файла, например, для дальнейшей обработки табличным процессором.

56
4. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ СВЕРХПРОВОДЯЩИХ ЭЛЕМЕНТОВ ГРАВИИНЕРЦИАЛЬНОГО ДАТЧИКА
4.1. П р я м о у г о л ь н а я с в е р х п р о в о д я щ а я п л а с т и н а в о в н е ш - н е м м а г н и т н о м п о л е
С помощью разработанной СКМ было проведено двух- и трехмерное моделирование сверхпроводникового цилиндрического электромагнитного подвеса, а также решен ряд модельных задач. В частности, проведен расчет напряженности магнитного поля на поверхности прямоугольной сверхпроводящей
пластины (0.5 1 0.05 см), находящейся во внешнем магнитном поле H e ,
ориентированном под произвольным углом  к плоскости пластины [17]. Использовалась формулировка, допускающая бесконечные элементы. Количество узлов, умещающихся вдоль ребер пластины – 60, 120 и 16. Число степеней свободы – 130 тыс. Были решены три конечноэлементные задачи для трех взаимно перпендикулярных направлений вектора напряженности магнитного поля – (1,0,0), (0,1,0), (0,0,1). Напряженность поля в произвольной точке определяется выражением
к плоскости пластины [17]. Использовалась формулировка, допускающая бесконечные элементы. Количество узлов, умещающихся вдоль ребер пластины – 60, 120 и 16. Число степеней свободы – 130 тыс. Были решены три конечноэлементные задачи для трех взаимно перпендикулярных направлений вектора напряженности магнитного поля – (1,0,0), (0,1,0), (0,0,1). Напряженность поля в произвольной точке определяется выражением
H (x, y, z) H e H e1 V1 H e2 V2 H e3 V3 ,
где Hei (i = 1, 2, 3) – компоненты вектора H e , Vi – магнитный потенциал соот-
ветствующей задачи. Если начало координат выбрать в центре пластины, а оси направить параллельно граням пластины, то ввиду симметрии для каждой задачи достаточно ограничиться рассмотрением лишь четверти исходной области.
Вычислен момент сил, действующий на пластину со стороны поля, в зависимости от угла . С целью выяснения допустимости использования двумерных расчетов для тонких, широких, но достаточно коротких образцов проведен соответствующий вычислительный эксперимент. Выполнен расчет для беско-
нечно длинной вдоль оси z пластины шириной 1 см и толщиной 0.05 см, накло-
ненной под углом = 30 относительно H e . Сделан вывод о том, что двумерное
моделирование позволяет получить лишь качественную оценку напряженности поля и момента сил.
4.2. М о д е л и р о в а н и е с в е р х п р о в о д н и к о в о г о ц и л и н д р и ч е - с к о г о э л е к т р о м а г н и т н о г о п о д в е с а
В статье [23] представлены результаты компьютерного моделирования цилиндрического сверхпроводникового электромагнитного подвеса, являющегося упрощенным вариантом чувствительных элементов криогенных гравиинерциальных датчиков. Принципиальная схема подвеса представлена на рис. 26, а). Он состоит из сверхпроводникового пробного тела 1, выполненного в виде полого цилиндра с технологическим отверстием в центре его дна, плоской однослойной сверхпроводниковой катушки 2 и цилиндрической однослойной

57
сверхпроводниковой катушки 3, намотанных на каркасе 4 из гиперпроводника. Катушки 2 и 3 соединены последовательно и образуют единую короткозамкнутую сверхпроводящую цепь (рис. 26, б)) с тепловым ключом 1 и контактами для запитки током 2. При запитке их током I создается неоднородное магнитное поле, в котором, вследствие эффекта Мейсснера, осуществляется левитация сверхпроводникового пробного тела в некотором равновесном положении, соответствующем рабочему зазору d. Для экранирования от внешних магнитных полей подвес помещается в сверхпроводниковый экран в виде полого цилиндра с полусферическим дном.
Приведем основные параметры подвеса: плоская катушка – 35 витков, радиус внешний и внутренний 7.5 и 3.15 мм соответственно; цилиндрическая катушка – 40 витков, радиус 9.05 мм; длина боковой стенки пробного тела 10.6 мм, радиус 10 мм, радиус отверстия 2 мм; толщина стенок 0.4 мм; диаметр проволоки 0.1 мм. Масса пробного тела m = 3.85 г, момент инерции J относительно осей x, y J = Jx = Jy = 2.1 10–7 кг м2. Размеры экрана: радиус 20 мм, длина 77 мм, толщина стенок 2 мм.
Задача состоит в определении магнитного поля в рабочем объеме подвеса. Для этого необходимо решить уравнение Лапласа в почти замкнутой области с заданными скачками магнитного потенциала на поверхностях разреза. При расчете распределения магнитного поля витки катушек заменяются несвязанными кольцами, в каждом из которых протекает ток I = 1 А. На всех границах использовалось однородное условие Неймана. Естественно предполагать, что высокие градиенты потенциала имеют место вблизи сверхпроводящих элементов, поэтому сетка в этих местах использовалась более мелкая, чем на удалении; в промежутках между витками было размещено как минимум 5 узлов. Решение осесимметричной задачи с помощью МКЭ приводит к большому числу степеней свободы (свыше 30 тыс., тип элементов – квадратичный элемент Лагранжа 2-го порядка) из-за необходимости сильно измельчать разбиение вблизи витков.
|
1 |
z |
|
2 |
d |
|
|
|
3 |
4 |
|
|
|
|
|
|
r |
а б
Рис. 26. Принципиальная и электрическая схема цилиндрического сверхпроводникового электромагнитного подвеса

58
Рассчитаны индуктивность L и сила Fz, действующая на крышку подвеса, в зависимости от величины зазора d. Аналогичные расчеты выполнены для подвеса, в котором витки катушек заменены кольцами прямоугольного сечения, плотно прилегающими друг к другу. Такая аппроксимация соответствует случаю пренебрежения неоднородностью поля в ближайшей окрестности витков. Оказалось, что при этом интегральные характеристики подвеса меняются не слишком сильно, причем L и Fz имеют значения на 10–15% меньше, чем в случае учета геометрии структуры витков. Указанная замена обеспечивает сокращение числа степеней свободы почти в 3 раза.
Данное обстоятельство было использовано при анализе боковых и угловых смещений цилиндрического подвеса, когда задача становится трехмерной. Выберем декартовы координаты так: оси y и z совпадают соответственно с осями r и z на рис. 6, а, а ось x направлена перпендикулярно плоскости рисунка. Число степеней свободы конечноэлементной задачи – около 180 тыс. Получены зависимости индуктивности L, компоненты Fy, действующей на боковую стенку ПТ, осевой компоненты Fz и проекции момента сил на ось x в зависимости от величины ее бокового смещения y относительно равновесного положения, а также зависимости индуктивности L, компоненты момента сил Мx и компонент сил Fz , Fy в зависимости от угла поворота крышки вокруг оси x.
Проведен анализ полученных результатов для двух режимов работы подвеса: постоянного тока и постоянного магнитного потока. В режиме постоянного тока обобщенная сила, действующая вдоль координаты qi, определяется выражением:
Fi |
1 |
I |
2 |
L |
, i = 1, ..., 6, |
(81) |
2 |
|
qi |
||||
|
|
|
|
|
||
где L – индуктивность системы, координатам q1 , q2 , q3 |
соответствуют линей- |
|||||
ные степени свободы ПТ, q4 , q5 , q6 – угловым степеням свободы. При i = 1, 2, 3 в (81) понимаются силы Fq, действующие на ПТ по координатам q1 = x, q2 = y, q3 = z, а при i = 4, 5, 6 – моменты сил Мq при поворотах ПТ на углы q4 = , q5 = , q6 = вокруг осей q1 , q2 , q3 соответственно.
Матрица жесткостей подвеса, характеризующая отклик системы на возмущения по всем степеням свободы, определяется как
|
|
|
|
|
|
|
F |
1 |
I 2 |
|
2 L |
|
|
|
|
|
|
|
|
|
||||
|
cij |
|
|
|
|
|
|
i |
|
|
|
|
|
|
, i, j =1, ..., 6, |
(82) |
||||||||
|
|
|
|
|
q |
|
2 |
|
q |
q |
|
|||||||||||||
|
|
|
|
|
|
|
j |
|
|
j |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|||
и собственные частоты колебаний соответствующих степеней свободы – |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
cii |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fi |
|
|
|
, i = 1, 2, 3; |
|
|
fi |
1 |
|
|
cii |
|
, i = 4, 5, 6. |
(83) |
||||||||||
2 |
|
|
m |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
J |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При малых смещениях (z – z0 , x, y) и поворотах ( , , ) относительно положения равновесия (z0 , 0, ..., 0) с учетом осевой симметрии подвеса функцию L можно представить в виде разложения в степенной ряд с точностью до членов третьего порядка включительно:

59
L(x, y, z, , )= L 0 + a ( z – z 0 )+b (z – z 0 ) 2 + c (z – z 0 )3 +e ( x2 +y2 )+ f ( |
2 + 2 )+ |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
+ g (x +y )+h ( x2 +y 2 )(z – z 0 )+p ( |
|
|
|
2 + |
|
2 )(z – z 0 ), |
|
|
|
|
|
(84) |
||||||||||||||||||||||||||||
где a, b, c, e, f, g, h, p – коэффициенты разложения, L0 = L(0, 0, |
z0 , 0, 0). Подста- |
||||||||||||||||||||||||||||||||||||||||||
вив это выражение в (81), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Fz |
1 |
I |
2 |
a |
I |
2 |
b(z z0 ) |
3 |
I |
2 |
c(z |
|
|
z0 ) |
2 |
|
|
|
1 |
I |
2 |
h(x |
2 |
y |
2 |
) |
1 |
|
I |
2 |
p( |
2 |
2 |
) , (85) |
|||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Fx |
I |
|
2 |
ex |
|
1 |
|
|
I |
2 |
g , |
|
|
|
|
|
|
|
|
|
|
|
(86) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Fy |
I |
2 |
ey |
|
1 |
|
I |
2 |
g |
, |
|
|
|
|
|
|
|
|
|
|
|
(87) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
M x |
I |
2 |
|
f |
|
1 |
|
I |
2 |
gy , |
|
|
|
|
|
|
|
|
|
|
|
(88) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
M y |
I |
|
2 |
f |
|
1 |
|
|
I |
2 |
gx . |
|
|
|
|
|
|
|
|
|
|
|
(89) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из полученных путем решения конечноэлементных задач зависимостей
L = L(z), L = L(y), L = L( ), Fz = Fz(z), Fz = Fz(y), Fz = Fz( ), Fy = Fy( ), Mx = Mx( ),
Mx = Mx(y) можно найти все коэффициенты, применив интерполяционный метод с учетом выражений (84) и (85-89). Получены следующие значения коэффици-
ентов: L0 =11.6432 10–6 Гн, a = 6.354 10–3 Гн/м, b = –3.693 Гн/м2 , с = 2.062 103 Гн/м3 , e = –1.411 Гн/м2, f = –7.71 10–5 Гн, g = – 2 .30 10–2 Гн/м, h = 1.63 103 Гн/м3, p = 4.10 10–2 Гн/м.
Максимальный ток запитки цепи подвеса определим из условия, что он создает поле, которое ни в одной точке не превосходит первое критическое по-
ле. Поскольку при d = 0.45 мм и I = 1 А H1, max = 12020 А/м, Hc1 = Bc1/ 0 111400 А/м, максимальный ток запитки Imax = Hc1/H1, max 1 А = 9.27 А. Найдем максимальную подъемную силу (Fz)max, соответствующую этому току. Так как (Fz)max I 2max, то (Fz)max 0.316 Н. Такая сила удержит в поле силы тяжести массу ПТ,
приблизительно равную 32 г.
Аналогичным образом определим ток, при котором ПТ будет левитировать на расстоянии d = 0.45 мм: I d = 0 .45 = (mg/Fz)1/2 = 3.23 А. (Здесь g – ускорение свободного падения).
Элементы матрицы жесткостей вычисляются по формуле (82) в точке, соответствующей равновесному положению подвеса. Тогда для точки (0, 0, z0 ,0, 0) имеем:
czz = I 2 b , |
cxx = cyy =I 2 e , |
c |
= c = I 2 f , |
(90) |
cx |
= c x = cy = c y = I 2 |
g |
/2. |
(91) |
Все остальные элементы равны нулю. Таким образом, коэффициент b по абсолютной величине имеет смысл жесткости по координате z при токе в короткозамкнутой цепи подвеса I = 1 А. Аналогично, коэффициенты e и f определяют жесткость подвеса соответственно по боковым и угловым смещениям ПТ, а ко-
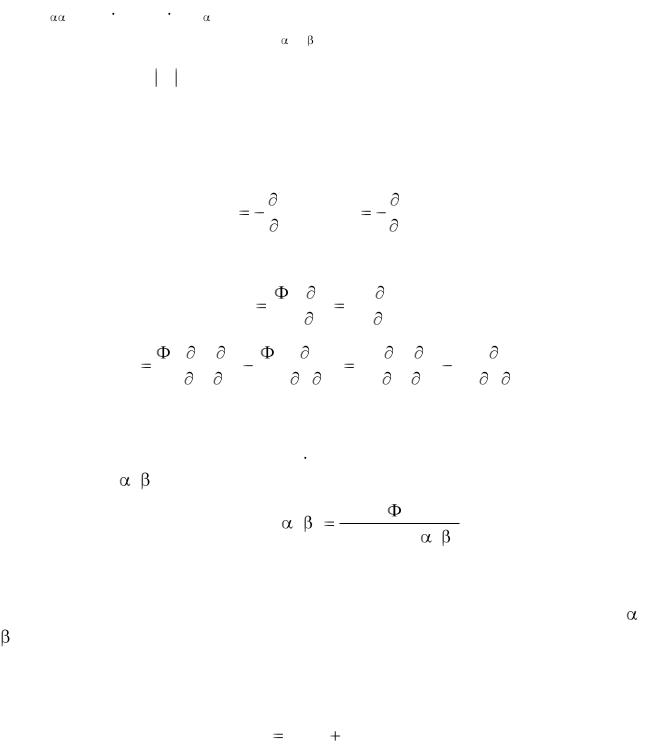
60
эффициент g характеризует перекрестную связь между соответствующими ли-
нейными и угловыми степенями свободы. |
|
|
Для тока I = 3.23 А, обеспечивающего подвешивание ПТ на |
высоте |
|
d = 0.45 |
мм, получим следующие значения жесткостей: czz =38.5 Н/м, |
cxx =14.7 |
Н/м, c |
=8.05 10–4 Н м, c y =0.12 Н. Вычислим также собственные частоты ко- |
|
лебаний: fz =15.9 Гц, fx =fy =9.8 Гц, f =f =9.9 Гц.
С увеличением высоты подъема ПТ жесткость czz убывает. Это видно из
выражения czz = I 2 ( b – 3c(z – z0 )) с учетом того, что c > 0.
Во втором из исследованных режимов поток Ф = LI, замороженный в короткозамкнутой цепи подвеса, постоянен. При изменении положения ПТ в цепи устанавливается такой ток, который препятствует изменению магнитного потока. Силу и жесткость найдем из общих формул
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|||
|
~ |
|
|
|
|
W |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
Fi |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Fi |
|
|
|
|
|
|
|
|
; |
|
|
cij |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
(92) |
||||||
|
|
|
|
|
qi |
|
|
|
|
|
q j |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где W = Ф2/2L – накопленная магнитная энергия. Итак, имеем |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
~ |
2 |
|
|
|
L |
|
|
I 2 |
|
L |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Fi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
(93) |
|
|
|
|
|
|
|
|
|
2L2 |
|
|
q |
|
2 |
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
~ |
2 L L |
2 |
|
|
|
|
|
2 L |
|
|
|
I 2 |
|
|
|
L L I 2 |
2 L |
|
|
|
||||||||||||||||||||
cij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(94) |
||
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
L q q |
|
|
2 q q |
|
||||||||||||||||||
|
L q q |
j |
2L q q |
j |
|
|
j |
|
j |
|
||||||||||||||||||||||||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|||||||||||
Пусть замороженный поток Ф0 соответствует равновесному положению при z = z0 (d = 0.45 мм). Тогда с учетом тока запитки, необходимого для подвешивание ПТ в таком положении, Ф0 = 4.07 10–5 Вб. Ток при смещениях и поворотах ПТ (z – z0 , x, y, , ) относительно положения (z0, 0, ..., 0) определится как
I ( x, y, z, , ) |
0 |
|
|
L( x, y, z, , ) . |
(95) |
||
|
Поскольку конечное выражение для силы (93) совпадает с аналогичным выражением, полученным для режима постоянного тока, то величины Fx , Fy, Fz,
Mx , My найдем по формулам (85-89), подставив вместо тока значение I(x, y, z, , |
|||||||||
~ |
|
при таком определении тока совпадают со |
|||||||
) из (95). Значения жесткостей cij |
|
||||||||
значениями cij , за исключением одного элемента матрицы – |
~ |
||||||||
czz , который отли- |
|||||||||
чается одним слагаемым I 2a2/L: |
|
|
|
|
|
|
|
|
|
~ |
|
2 |
|
|
I 2 |
2 |
|
|
|
|
|
|
|
||||||
czz |
I |
|
b |
|
|
a |
|
. |
(96) |
|
|
|
|
||||||
|
|
|
|
|
L |
|
|
|
|
Легко заметить, что ~zz > c . Подставив значения коэффициентов a и b для мо-
c zz
дели подвеса с учетом структуры витков катушек, получим czz = 72.0 Н/м и fz = 21.8 Гц. Полученные результаты необходимы для построения уравнений движения ПТ гравиинерциального датчика и выбора оптимальных режимов функционирования подвеса.
