
2788
.pdf
31
|
|
|
|
Препроцессор |
|
|
|
База данных и |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
библиотеки |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Файл данных задачи |
|
Файлы данных сетки |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
и геометрии области |
|
xr, yr, (zr) |
|
|
||||||||
|
nn1 |
|
|
|||||||||
|
taskinfo |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
potent |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решатель
Файлрешение rhs
Постпроцессор
Вспомогательные и сервисные программы
Рис. 7. Структура СКМ.
Задание параметров |
|
Ввод опорных точек, |
|
|
|||
задачи |
|
линий, поверхностей |
|
|
|
|
|
|
|
|
|
Деление области на зоны (подобласти),
Задание граничных и других условий, неоднородностей среды
Сохранение геометрии области, ГУ, неоднородностей
|
|
|
|
|
Проверка качества и |
|
|
|
|
|
|
||
Загрузка геометрии и |
|
Разбиение подобла- |
|
сохранение конечно- |
||
|
|
|||||
ГУ с диска |
|
стей на КЭ |
|
элементной сетки |
||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запуск процессора и |
|
|
|
|
|
|
решение задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ |
|
|
|
|
|
|
результатов |
|
|
|
|
|
|
|
|
Рис. 8. Последовательность действий при работе с СКМ.

32
Оболочка препроцессора
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Блок задания па- |
|
Блок построения |
|
Блок геометриче- |
|
Блок |
|||||||||
раметров задачи |
|
|
области |
|
ских операций |
|
визуализации |
||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Файл данных о задаче |
Блок дискретиза- |
Блок дискретиза- |
и геометрии области |
ции подобластей |
ции подобластей |
|
блочным методом |
методом Делоне |
Файлы данных конечно- |
|
|
элементной сетки |
|
|
Процессор |
|
|
Рис. 9. Обмен данными в препроцессоре
3.3.1. Препроцессор
Препроцессор обеспечивает подготовку исходных данных для решения двумерных, осесимметричных или трехмерных задач методом конечных элементов. Специфика МКЭ состоит в реализации следующих основных этапов: задание параметров задачи; ввод геометрии области, разбитой на ряд простых подобластей с учетом особенностей решаемой задачи; задание граничных и других условий, неоднородностей среды; разбиение каждой подобласти на конечные элементы с заданной плотностью узлов; проверка качества сети и сохранение данных на диске. Препроцессор состоит из нескольких функциональных блоков, которые связаны в единое приложение посредством программного интерфейса (рис. 9).
Блок задания параметров задачи
Данный блок позволяет определить тип дифференциального уравнения, которому удовлетворяет искомая функция; стационарная или нестационарная задача; двумерная, осесимметричная или трехмерная. В общем случае дифференциальное уравнение имеет вид:
|
2 u |
|
u |
|
|
(r ,t) |
|
(r ,t) |
|
( (u, u,r ,t) u) |
f (u,r ,t) , |
t 2 |
t |

|
|
33 |
где |
|
– неизвестная функция, вид функций , , и f определяется |
u u(r ,t) |
пользователем. Данное уравнение имеет достаточно общий вид. В частном случае, когда = = f = 0, получим уравнение Лапласа:
если
если
если
|
|
( (u, u,r ,t) u) 0; |
|
|
|
= |
= 0, а f |
0, то уравнение Пуассона: |
|
|
|
|
|
|
|
; |
|
|
|
( (u, u,r ,t) u) |
f (r ,t) 0 |
|
|
= |
= 0, а f |
|
|
|
|
u w(r , t) , то уравнение Гельмгольца: |
|||||
|
|
|
|
|
; |
|
|
( (u, u,r ,t) u) |
u w(r , t) 0 |
||
= 0, а  0 и f 0, то уравнение диффузии (теплопроводности):
0 и f 0, то уравнение диффузии (теплопроводности):
|
u |
|
|
(r ,t) |
|
( (u, u,r ,t) u) |
f (u,r ,t) . |
t |
В случае, когда все четыре функции отличны от нуля, имеем уравнение волнового типа, приведенное выше.
Кроме этого, в данном блоке осуществляется ввод граничных и других условий. На линии (поверхности) Г могут быть заданы либо граничное условие Дирихле (условие 1 рода):
u(r ,t)
либо условие Неймана (2 рода):
u
n
либо смешанное (3 рода):
q(u,r ,t) ,
q(u, r ,t) ,
|
|
|
u |
|
|
|
|
||||||
(u, u,r ,t) u(r ,t) |
(u,r ,t) |
|
|
q(u,r ,t) . |
||
n |
||||||
|
|
|
|
|
||
Помимо этого, могут быть заданы следующие типы условий:
–скачка (“разреза”);
–периодическое;
–условие симметричности;
–условие постоянства потока.
Для нестационарных задач необходимо, кроме этого, задавать начальные условия – значения функции и ее производной в момент времени t = 0. Начальные условия имеют вид:
u |
|
t 0 U (r ); |
u |
|
V (r ) . |
|
|||||
|
t |
||||
|
|
t 0 |
|||
|
|
|
|
||
|
|
|
|
|
Также в блок входят функции задания неоднородностей среды. Если область задачи содержит физически различающиеся среды, то границы подобластей должны проходить по линиям (поверхностям) раздела сред. Подобласти, в которых задана неоднородность, может отличаться от остальной области зада-
34
чи либо видом по крайней мере одной из четырех функций, входящих в уравнение, либо (для нестационарных задач) видом начального условия.
Конкретный вид функций, входящих в уравнение, граничные и начальные условия задается с помощью специального шаблона. Каждая функция в рамках данного препроцессора может быть представлена в виде комбинации трех более простых функций из базового набора:
константа (f = C);
полином (f = Axn + Bxn–1y + … + Cyn + … + Dx + Ey + F или f = Aun + + Bun–1 + … + C);
экспонента (f = AeBx + Cy + D или f = AeBu + C);
тригонометрические функции (f = Asin(Bx + Cy + D) + Ecos(Fx + Gy + H) или f = Asin(Bu + C) + Dcos(Eu + F));
степенная (f = AxB +CyD или f = AuB).
Выбрав вид функции, пользователь вводит с клавиатуры значения ее коэффициентов.
Эти элементарные функции являются функциями только одной перемен-
ной (либо только r , либо только t, и т. д.). Они соединяются между собой операциями:
сложения (f1 + f2); умножения (f1 * f2); деления (f1 / f2);
функциональной зависимости (f1(f2)).
Блок построения области
Любые двухили трехмерные области, какими бы сложными они ни были, могут быть представлены в виде совокупности более простых подобластей (зон), границами которых являются кривые (поверхности) 1 и 2 порядка. Форма этих подобластей не должна сильно отличаться от выпуклой, а длины ребер, образующих зону, должны быть соразмерны. В противном случае качество конечноэлементной сетки в этой зоне будет весьма плохим, поскольку размеры элементов в пределах одной зоны не могут сильно различаться между собой. Подобный подход позволяет получить качественную сетку даже для областей, размеры составных частей которых отличаются на порядки.
Вданном препроцессоре могут быть заданы зоны двух типов, в соответствии с двумя имеющимися способами разбиения их на конечные элементы. Зоны первого типа имеют форму четырехугольника (шестигранника), и для их задания достаточно указать номера двух противолежащих линий (поверхностей). Для задания зон второго типа необходимо перечислить номера всех линий (поверхностей), ограничивающих зону, поскольку их число не ограничено.
Вдальнейшем подобласти разбиваются по отдельности, что облегчает пользователю контроль качества конечноэлементной сетки, управление плотностью распределения узлов, а также сильно упрощает алгоритм дискретизации.
Порядок построения области включает следующие основные этапы. Сначала вводится ряд узловых точек (вершин), задающих размеры области и пред-

35
полагаемое деление ее на зоны. Затем эти точки соединяются линиями (прямыми либо кривыми второго порядка, в том числе дугами окружностей). Параметрическое уравнение линии 2 порядка, проходящей по трем узлам (x1, y1), (x2, y2), (x3, y3), можно представить следующим образом:
x |
t(1 t) |
x |
(1 t 2 )x |
|
t(1 t) |
x |
|
, y |
t(1 t) |
y |
|
(1 t 2 ) y |
|
t(1 t) |
y |
|
, |
|
2 |
|
3 |
|
1 |
2 |
|
3 |
|||||||||
|
2 |
1 |
|
2 |
|
|
2 |
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где параметр t лежит в интервале [–1, 1]. Параметрическое уравнение дуги окружности с центром (x0, y0) и радиусом R:
x |
x0 |
R cos 1 |
1 t |
|
1 t |
, y y0 |
R sin 1 |
1 t |
|
1 t |
, 1 t 1, |
||
2 |
2 |
|
2 |
2 |
2 |
|
2 |
||||||
|
|
|
|
|
|
|
|
||||||
где |
1 и |
2 – соответственно начальный и конечный углы дуги в радианах. |
|||||||||||
После этого из линий образуются поверхности (патчи), которые в трехмерном случае могут представлять собой поверхности второго порядка (элементы цилиндра, конуса, сферы). В случае двумерной или осесимметричной задачи на этом этапе построение области заканчивается, а для трехмерных задач из этих патчей конструируются, наконец, трехмерные подобласти (зоны), которые уже готовы к разбиению на конечные элементы.
Пусть, например, расчетная область задачи представляет собой прямоугольник с круглым отверстием в середине (рис. 10). Из соображений симметрии достаточно построить четверть области и разбить ее на зоны (рис. 12).
Рис. 10. Расчетная область задачи |
Рис. 11. Меню ввода линий |
Рис. 12. Ввод геометрии области
Блок геометрических операций
Функции этого блока обеспечивают простоту и легкость модификации расчетной области, что часто бывает необходимо при решении задач моделиро-

36
вания, а также облегчают построение сложных областей с повторяющимися структурами (такими, как витки катушки). К геометрическим операциям относятся:
сдвиг; параллельный перенос (копирование объекта); поворот-сдвиг;
поворот-копирование; зеркальное отражение; гомотетия.
Рис. 13. Пример зеркального отображения при построении области.
Все эти операции могут быть применены к узловым точкам (вершинам), линиям, поверхностям и подобластям (зонам). Кроме этого, по желанию пользователя ряд линий (в трехмерном случае поверхностей) можно объединить в один объект, который также можно сдвигать, поворачивать и т.д. одной командой, не перечисляя его составных частей.
Блок визуализации
Функции блока визуализации обеспечивают отображение вводимой области задачи в удобном для пользователя виде (рис. 14). Предусмотрены:
сдвиг изображения и изменение его масштаба; ограничение отображаемой части области по любой из координат;
повороты области относительно луча зрения (для трехмерных областей); разрешение/запрещение отображения номеров объектов; отображение краевых и других условий,
отображение конечно-элементной сетки, номеров узлов и элементов, и др.

37
Также ввиду сложности реальных трехмерных областей имеется возможность отображения только той части области, которая попадает
внутрь |
слоя заданной |
толщины |
|
вблизи |
заданной |
плоскости |
|
A x + B y + C z + D = 0, а |
также |
воз- |
|
можность активировать/деактиви- |
|||
ровать отдельные объекты. |
Рис. 14. Меню “Опции” |
||
Блоки дискретизации подобластей
Генерация конечноэлементной сетки является наиболее важным этапом работы препроцессора, так как слишком редкая или некачественная сеть может привести к большим погрешностям решения задачи, а слишком частая – к неоправданным затратам машинного времени на этапе вычислений. Разбиение должно быть проведено без пропусков и перекрытий, при этом форма конечных элементов должна не очень сильно отличаться от правильной. При проведении разбиения следует учитывать априорную информацию о поведении неизвестной функции u: там, где предполагается быстрое изменение u (например, вблизи неоднородностей, острых углов и т.п.), сеть должна быть более густой, там, где изменение u должно быть медленным – более редкой.
Существует несколько основных типов алгоритмов дискретизации. Наиболее простым является блочный метод, с помощью которого можно разбивать четырехугольные подобласти (в трехмерном случае – шестигранные). Недостатком данного подхода является то, что число узлов на противолежащих сторонах (гранях) должно быть строго одинаковым, что сильно затрудняет управление плотностью распределения узлов сетки. К достоинствам метода относится высокое качество получаемой конечноэлементной сетки, а также простота его программной реализации.
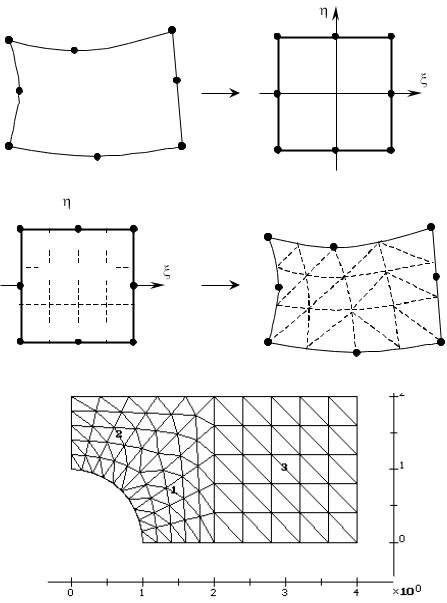
Рассмотрим алгоритм разбиения зон блочным методом для двумерной задачи. В общем случае зона представляет собой четырехугольник, стороны которого могут быть кривыми второго порядка (рис. 15). Представим эту зону в виде одного четырехугольного изопараметрического конечного элемента 2-го порядка. Как известно, подобный криволинейный элемент можно свести к некоторому стандартному четырехугольному элементу – квадрату; при этом от декартовых координат (x, y) мы переходим к локальным координатам ( , ). Локальные координаты ( , ) в пределах элемента изменяются от –1 до 1, и, зная, на сколько частей необходимо разделить стороны зоны, легко определить локальные координаты узлов сети на линиях и внутри зоны (рис. 15). Затем по этим локальным координатам легко найти декартовы координаты узлов сети:
x |
Nm (ξ, ) X m , y |
Nm (ξ, )Ym , |
|
m |
m |
где Xm и Ym – декартовы координаты узлов зоны, {Nm} – функции формы для четырехугольного изопараметрического элемента 2-го порядка. В результате зона окажется разбитой на четырехугольники, которые могут быть в свою оче-
38
редь поделены пополам меньшей диагональю для получения треугольных конечных элементов. Узлы сети нумеруются и из них формируются списки, которые и задают конечные элементы. Если на какой-либо из линий зоны уже имеются узлы сети (соседняя зона уже разбита), то новые узлы на этой линии не создаются, а используются уже существующие. Таким образом происходит автоматическое сшивание сетей в соседних зонах. В случае трехмерных областей зона представляется в виде изопараметрического гексаэдрального элемента 2 порядка, который делится на гексаэдры, и каждый из них, если необходимо, на пять или шесть тетраэдров.
Пример разбиения зон блочным методом показан на рис. 16.
|
|
1 |
|
|
|
7 |
6 |
5 |
|
–1 |
8 |
|
4 |
1 |
|
1 |
2 |
3 |
|
|
|
–1 |
|
|
 1
1
7 
 6
6  5
5
–1  8
8 



 4
4  1
1
1 
 2
2  3
3
 –1
–1
Рис. 15. Дискретизация четырехугольной зоны блочным методом.
Рис. 16. Пример разбиения зон блочным методом.
Методом Делоне (рис. 17) можно разбивать зоны произвольной формы, причем число узлов на каждой стороне (грани) может быть любым. Дискретизация области начинается с двух треугольников (в трехмерном случае – с вось-

39
ми тетраэдров), причем фигура, образованная этими начальными элементами, должна полностью содержать внутри себя разбиваемую зону. Далее начинается последовательное внедрение в первоначальное разбиение новых узлов, при этом после внесения каждого нового узла сеть перестраивается. Те элементы, для которых описанная окружность (сфера) будет содержать внутри себя новый узел, удаляются, и вместо них создаются новые с участием нового узла. Первыми обычно вносятся узлы, лежащие на границах зоны, затем – внутренние узлы. Существует большое количество разновидностей метода Делоне, различающихся алгоритмами вычисления координат новых внутренних узлов. В данном препроцессоре реализован алгоритм, предусматривающий построение “центрального” узла, координаты которого вычисляются с учетом плотности разбиения границ зоны. Затем строятся отрезки, соединяющие центральный узел с углами зоны. Эти отрезки разбиваются на одинаковое число частей (ребер), получившиеся при этом узлы соединяются отрезками так, что образуется ряд вложенных фигур, являющихся (приближенно) образами внешней границы при гомотетии относительно центрального узла. Стороны этих вложенных фигур также делятся на части, так, чтобы их длина не отличалась сильно от длины ранее созданных ребер. Все полученные таким образом узлы вносятся в конечноэлементную сеть по алгоритму Делоне, рассмотренному выше. Затем элементы, которые расположены вне границ области, удаляются.
После добавления всех узлов происходит оптимизация полученной сети путем перемещения каждого внутреннего узла в барицентр фигуры, образованной элементами с участием этого узла (рис. 18). Эту процедуру можно провести несколько раз, в результате качество сети, как правило, заметно улучшается.
Недостатками такого алгоритма является то, что, во-первых, разбиваемая зона должна быть односвязной, и форма ее не должна сильно отличаться от выпуклой, и во-вторых, числа разбиения на линиях зоны должны не очень сильно отличаться друг от друга. Тем не менее, данный подход позволяет получить весьма качественную сеть, а указанные ограничения не приносят значительных неудобств для пользователя.
а) |
б) |

40
в) г)
г)
Рис. 17. Этапы дискретизации зоны методом Делоне. а) начальное разбиение (2 конечных элемента); б) добавлен 1-й из узлов будущей сети; в) добавлены все узлы сети; г) удалены лишние элементы (расположенные вне зоны) и проведена оптимизация расположения внутренних узлов.
Рис. 18. Локальная оптимизация сети путем перемещения общего для нескольких элементов узла в барицентр образованной ими фигуры.
В тех случаях, когда конечноэлементная сеть в одной или нескольких зонах оказалась недостаточно хорошего качества, она может быть удалена и сгенерирована заново. Критерием качества треугольного (тетраэдрального) конечного элемента является отношение радиусов вписанной и описанной окружностей (сфер): k = r/R. Максимально возможной величиной для этого отношения, как известно, является k = 1/2 для треугольника и k = 1/3 для тетраэдра. Если для рассматриваемого элемента эта величина оказывается меньше 0.25 (0.1), то данный элемент признается плохим, и сеть в этом месте должна быть улучшена с помощью специальных алгоритмов.
а |
б |
в |
Рис. 19. “Хороший” (а) и “плохие” (б, в) треугольные конечные элементы
