
2788
.pdf
21
Другой подход связан с добавлением к функционалу дополнительного интеграла по границе Г1
F ( ) |
1 |
( )2 |
2 |
2 f d |
1 |
|
|
||||
2 |
|
2 |
|||
|
|
|
|
2 g3 d |
( g1 )2 d . (49) |
3 |
1 |
Чем больше выбирается параметр , тем точнее удовлетворяется граничное условие 1 рода. В такой формулировке данное условие является естественным, так как функция , доставляющая минимум функционалу (49) на базе любых функций из определенного класса, одновременно является решением краевой задачи.
Граничные условия 2 рода являются частным случаем условий 3 рода при = 0. Поэтому функционал (49) может использоваться как для краевой задачи 3 рода, так и 2 рода. Граничные условия Неймана и смешанные при таком выборе функционала являются естественными. Если в функционале отсутствует интеграл по Г2 или по Г3, то конечно-элементное решение на данной границе будет
удовлетворять однородному краевому условию Неймана:
0 .
n
Этот результат имеет значение с практической точки зрения: для обеспечения однородного условия 2 рода вообще не следует задавать никаких условий на границе.
2) Граничные условия на границе раздела физически различающихся
сред.
В задачах электромагнетизма часто ставятся условия типа
|
|
|
1 |
|
2 |
, |
|
(50) |
||
1 |
n |
2 |
n |
|
|
|||||
|
|
|
|
|
|
|
|
|||
1 |
|
|
2 |
, |
или |
|
= |
|
, |
|
|
|
|
|
1 |
2 |
|||||
|
|
|
|
|
|
|
|
|
||
где 1 и 2 – значения потенциала на двух различных сторонах поверхности,
1 , 2 – свойства сред.
Покажем, что решение уравнения Пуассона 
 = – f, полученное по обычной схеме МКЭ, автоматически удовлетворяет этим условиям.
= – f, полученное по обычной схеме МКЭ, автоматически удовлетворяет этим условиям.
Рассмотрим два треугольных элемента, которые имеют общую границу, совпадающую с линией раздела сред (см. рис. 3). Запишем уравнения для невязок в области и на границе раздела:
S1 |
S2 |
|
|
1 S |
2 |
S1 |
S2 |
Рис. 3.
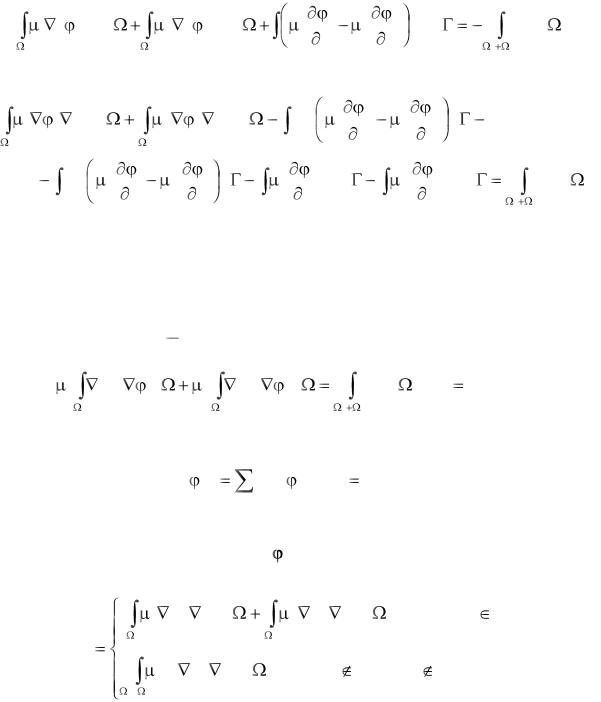
22
|
2 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
||
|
1Wm d |
|
|
2Wm d |
|
|
|
|
|
|
|
Wm d |
|
fWm d . |
||||||||||
1 |
|
|
2 |
|
|
1 |
|
n |
2 |
|
n |
|
||||||||||||
1 |
|
|
|
|
2 |
|
|
|
S |
|
|
|
|
|
|
|
|
1 |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Первые два интеграла перепишем по формуле Грина |
|
|
||||||||||||||||||||||
|
|
W d |
|
|
|
|
W d |
|
W |
|
|
|
1 |
|
|
|
2 |
|
d |
|
||||
1 |
1 |
|
2 |
|
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|||||||||
|
m |
|
|
m |
|
m |
|
n |
|
n |
|
|
||||||||||||
1 |
|
|
|
|
2 |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
|
|
2 |
|
|
|
||||||
|
Wm 1 |
|
|
d |
|
Wm d |
|
|
|
|
Wm d |
fWm d . |
||||||||||||
|
n |
2 |
|
n |
1 |
n |
|
2 |
|
n |
||||||||||||||
|
S |
|
|
|
|
|
S1 |
|
|
|
|
|
S2 |
|
|
1 2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Последние два интеграла в левой части уравнения можно опустить, поскольку если S1 и/или S2 является частью границы Неймана, то они уничтожа-
ются путем добавления соответствующей невязки. Если же S1 , S2 – границы с
соседними элементами с теми же самыми свойствами среды, то вследствие равенства нормальных производных эти интегралы также исчезают. В итоге, вы-
брав базисные функции W = W , получим
m m
1 Wm |
1d |
2 |
Wm |
|
2 d |
|
fWm d |
, |
m 1,... , M . |
1 |
|
|
2 |
|
|
1 |
2 |
|
|
Проводя аппроксимацию на конечных элементах обычным способом |
|||||||||
|
|
(e) |
N |
(e) |
(e) , |
e 1, 2, |
|
|
|
|
|
|
m |
m |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
получим систему |
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
= F, |
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
1 Ni |
Wj d |
|
2 Ni |
Wj d , |
если i, j S |
|||
1 |
|
|
|
2 |
|
|
|
|
|
Sij |
|
|
|
|
|
|
|
|
|
|
1(2) |
Ni |
Wj d , |
|
если i |
|
S (или j |
S) |
|
1 ( |
2 ) |
|
|
|
|
|
|
|
|
что соответствует стандартным конечноэлементным выражениям с поправкой на неоднородную среду.
3)Скачок потенциала на поверхности разреза Решение задач для сверхпроводниковых многосвязных систем требует
учета условия скачкообразного изменения потенциала на некоторой поверхности разреза (8). Рассмотрим соответствующую модификацию системы линейных алгебраических уравнений МКЭ для задачи Лапласа.
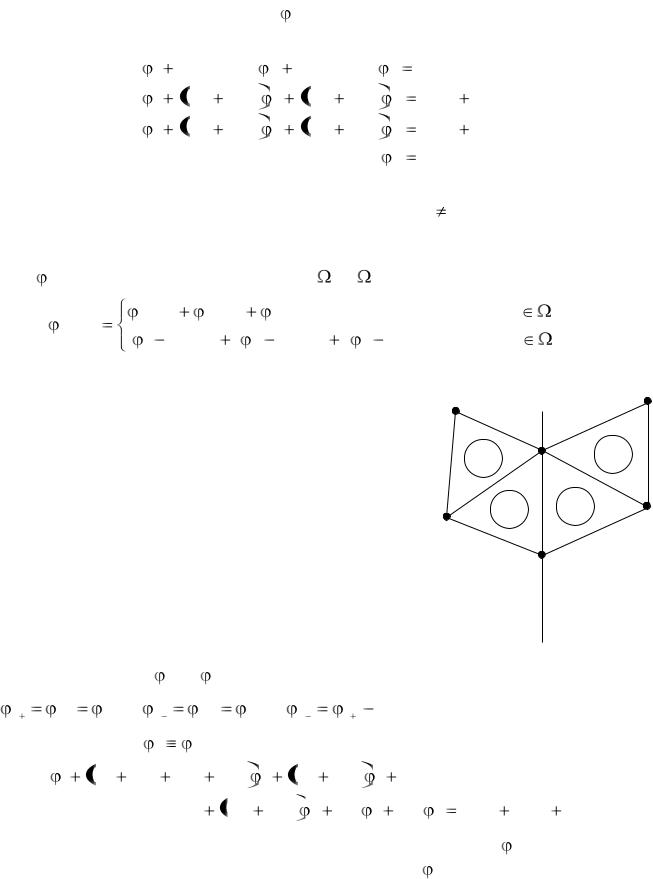
Пусть два смежных конечных элемента (треугольника) имеют общую сторону, лежащую на линии S (рис. 5). Выпишем отдельно линейную систему уравнений для обоих элементов:

|
|
|
|
|
23 |
|
S (1) |
(1) |
0; |
S (2) |
(2) |
0 . |
2 |
ij |
i |
|
ij |
i |
|
|
|
|
|
||||
i {1,2,3} |
|
|
i {3,2,4} |
|
|
|
Следуя |
стандартному |
методу |
конечных |
|
|
|
элементов [10], проведем объединение этих сис- |
|
4 |
||||
1 |
2 |
|||||
тем. Если S не является линией разреза, то в узлах |
||||||
1 |
|
|||||
2 и 3 должно выполняться условие непрерывно- |
|
|||||
|
|
|||||
сти, т.е. |
|
|
|
|
3 |
|
(1) |
(2) |
0, |
|
S |
|
2 |
2 |
(51) |
|
||
(1) |
(2) |
0. |
Рис. 5 |
|
|
|
|
||||
|
|
|
|
||
3 |
3 |
|
|
|
|
В этом случае получается система (с учетом обозначений i |
i(l)) |
||||
S (1) |
|
|
S (1) |
|
|
S (1) |
|
|
|
11 |
1 |
|
12 |
2 |
|
13 |
3 |
|
|
S (1) |
|
S (1) |
S (2) |
|
S (1) |
S (2) |
|
S (2) |
|
21 |
1 |
22 |
22 |
2 |
23 |
23 |
3 |
24 |
4 |
S (1) |
|
S (1) |
S (2) |
|
S (1) |
S (2) |
|
S (2) |
|
31 |
1 |
32 |
32 |
2 |
33 |
33 |
3 |
34 |
4 |
|
|
|
S (2) |
|
|
S (2) |
|
S (2) |
|
|
|
|
42 |
2 |
|
43 |
3 |
44 |
4 |
0
0
(52)
0
0.
Если на S происходит скачок, то каждому узлу, лежащему на S, необходимо поставить в соответствие два значения потенциала i+ и i– . Одно из этих значений будет относиться к элементам, лежащим по одну сторону от S, другое
– к элементам, лежащим по другую сторону относительно S. В нашем случае условие скачка можно записать в виде
(1)(2)
2 2
(1)(2)
3 3
I ,
(53)
I.
|
При объединении элементов для каждого узла на S следует оставить |
||||||||
только |
одну независимую переменную, например, |
2 |
(1) |
, |
3 |
(1) |
, а |
||
|
|
|
|
2 |
|
3 |
|
||
(2) |
и |
(2) |
заменить соответственно выражениями 2 – I, 3 |
– I. |
|
|
|
|
|
2 |
3 |
|
|
|
|
||||
В итоге получим систему
S (1) |
|
|
S (1) |
|
|
S (1) |
|
|
|
11 |
1 |
|
12 |
2 |
|
13 |
3 |
|
|
S (1) |
|
S (1) |
S (2) |
|
S (1) |
S (2) |
|
S (2) |
|
21 |
1 |
22 |
22 |
2 |
23 |
23 |
3 |
24 |
4 |
S (1) |
|
S (1) |
S (2) |
|
S (1) |
S (2) |
|
S (2) |
|
31 |
1 |
32 |
32 |
2 |
33 |
33 |
3 |
34 |
4 |
|
|
|
S (2) |
|
|
S (2) |
|
S (2) |
|
|
|
|
42 |
2 |
|
43 |
3 |
44 |
4 |
0
IS IS IS
(2) |
IS (2) |
|
22 |
23 |
|
(2) |
IS (2) |
(54) |
32 |
33 |
|
(2) |
IS (2) . |
|
42 |
43 |
|
Таким образом, по сравнению с (52) данная система отличается только правой частью. Решений она не имеет (объясните, почему?). Для получения нужного решения следует заметить, что дополнительное условие (8) накладывается только на разность значений потенциала, а не на саму функцию. Тем самым, решение задачи определяется с точностью до константы. Поэтому необходимо в одном каком-либо узле зафиксировать потенциал, т. е. придать ему
24
вполне определенное значение, которое играет роль начала отсчета. Например, поставим в узле 4 условие
4 = 0.
Тогда система примет вид
S (1) |
|
|
S (1) |
|
|
S (1) |
|
0 |
|
|
|
11 |
1 |
|
12 |
2 |
|
13 |
3 |
|
|
|
|
S (1) |
1 |
S (1) |
S (2) |
2 |
S (1) |
S (2) |
3 |
IS (2) |
IS (2) |
|
|
21 |
22 |
22 |
23 |
23 |
|
22 |
23 |
(55) |
|||
S (1) |
|
S (1) |
S (2) |
|
S (1) |
S (2) |
|
IS (2) |
IS (2) |
||
31 |
1 |
32 |
32 |
2 |
33 |
33 |
3 |
|
32 |
33 |
|
|
|
|
|
|
|
|
4 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь система имеет отличный от нуля определитель. В случае, если I = 0 |
|||||||||||
(скачка нет), ее решение – тождественный нуль, если I |
0 (скачок есть), полу- |
||||||||||
чим искомое ненулевое решение задачи.
По итогам решения системы конечноэлементных уравнений найдем зна-
чение в произвольной точке элементов |
1 и |
2 |
согласно ( ): |
|
|||||
(x, y) |
1 N1(1) |
2 N |
2(1) |
3 N3(1) , |
|
|
если (x, y) |
1 , |
|
( 1 |
I )N1(2) |
( 2 |
I )N2(2) |
( |
|
I )N3(2) , если (x, y) |
2 . |
||
|
3 |
||||||||
Рассмотренная процедура формирования глобальной конечноэлементной системы обобщается на любое число конечных элементов. Особое внимание следует уделить случаю, когда узел, лежащий на S, принадлежит более чем двум конечным элементам. Такому узлу по-прежнему будут соответствовать только две переменные, каждая из которых связана с элементами, лежащими по определенную сторону относительно линии (поверхности) разреза.
Добавим к элементам 1 и 2 (рис. 5) еще два элемента, как показано на рис. 6. Выпишем второе уравнение глобальной системы; это уравнение соответствует узлу 2, который лежит на S и является общим для всех четырех элементов. С этим узлом связаны потенциалы 2+ и 2– , причем
|
6 |
5 |
|
|
2 |
3 |
4 |
|
|
1 |
2 |
1 |
4 |
|
|
|
3 |
+ –
S
Рис. 6
|
(1) |
(3) |
, |
|
(2) |
|
(4) , |
|
|
I. |
|
|
|
2 |
2 |
2 |
|
2 |
2 |
|
2 |
|
2 |
2 |
|
|
|
Вводя обозначение 2 |
2+ , получим следующее уравнение |
|
|||||||||||
S (1) |
|
S (1) |
|
S (2) |
S (3) |
S (4) |
|
S (1) |
S (2) |
|
|
|
|
21 |
1 |
22 |
|
22 |
22 |
22 |
2 |
|
23 |
23 |
3 |
|
|
|
|
|
|
|
|
S24(2) |
S24(4) |
4 |
S25(3) |
5 S26(4) |
6 S22(2) I |
S22(4) I S23(2) I . |
|
Сформировав остальные уравнения и положив, например, |
4 = 0, получим |
||||||||||||
новую систему, решение которой даст набор чисел { |
i}. При вычислении по- |
||||||||||||

25
тенциала внутри элементов 1 и 3 в качестве узлового значения узла 2 следует брать 2 , а внутри элементов 2 и 4 – величину ( 2 – I ).
Плоская формулировка легко переносится на трехмерную геометрию использованием объемных конечных элементов и поверхностей разреза, проведенных по тем же правилам, что и линии разреза.
При проведении разрезов следует учитывать следующее:
1)при обходе любого замкнутого контура суммарный скачок потенциала должен быть равен полному току внутри этого контура. Важно при использовании метода конечных элементов согласовывать знаки скачков. Так, токи считаются одного знака, если при обходе контуров, охватывающих каждый ток, в одном направлении, например против часовой стрелки, совпадают знаки полного изменения потенциала на разрезах;
2)форма поверхностей (линий) разреза может быть любой, но нельзя допускать их пересечения и прерывистости;
3)существует множество способов задания разрезов, но наиболее универсальными являются: а) в двумерном варианте разрез соединяет либо сверхпроводник с другим сверхпроводником, либо сверхпроводник с внешней границей.
Впервом случае считается, что в обоих сверхпроводниках текут одинаковые по величине, но разные по направлению токи; б) в трехмерном варианте поверхность разреза со скачком, равным току, закрывает отверстие каждого сверхпроводникового контура, либо проводится от контура до внешних границ.

26
3. СИСТЕМА КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ СВЕРХПРОВОДЯЩИХ ЭЛЕМЕНТОВ ГРАВИИНЕРЦИАЛЬНЫХ ДАТЧИКОВ
3.1. О с н о в н ы е ф и з и к о - м а т е м а т и ч е с к и е м о д е л и с в е р х п р о - в о д я щ е г о п о д в е с а
Проведенный анализ литературы показывает, что используемые аналитические расчеты СЭМП мало пригодны для расчета реальных схем подвесов. Это связано с трудностями интегрирования уравнений магнитостатики для тел сколько-нибудь сложной формы. Поэтому приобретают актуальность методы расчета характеристик подвесов на основе численного анализа полей.
В обобщенном виде модель СЭМП представляет собой замкнутую электромеханическую систему, состоящую из подвижного пробного тела, сверхпроводниковых катушек, каркаса, сверхпроводникового экрана и металлических несверхпроводящих колец (деталей корпуса) для демпфирования колебаний.
Рассмотрены математические модели для описания процессов в конструктивных элементах СЭМП, которые можно обобщить системой дифференциальных уравнений
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
( |
, r ) |
|
|
( |
, r ) |
f ( |
, r , t) |
в области |
|
; |
|
|
(56) |
||||
|
|
|
|
t |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(r, t) |
на границе Г; |
|
|
|
|
|
|
(57) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(r, t) |
q(r, t) |
на границе Г2; |
|
|
|
|
(58) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
0 (r ) |
при t = t0, |
|
|
|
|
|
|
|
(59) |
||||
где Г |
1 |
+ Г |
2 |
= Г – граница замкнутой области |
; , , |
, f, , q, |
0 |
, – |
0 |
– заданные |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T0. В случае векторной задачи |
|||||||
функции; |
|
– неизвестная функция; ( r |
, t) |
||||||||||||||||||
(56-59) ставится дополнительное условие div |
= 0. Кроме того, возможны до- |
||||||||||||||||||||
полнительные условия, накладываемые на разность значений функции |
в не- |
||||||||||||||||||||
которых точках области (условия скачка, сдвига и др.), или в виде интегральных соотношений.
Остановимся подробнее на формулировке задачи расчета магнитного поля для сверхпроводникового подвеса. Будем рассматривать только СЭМП, работающие в мейсснеровском режиме. В общем случае требуется найти распре-
деление напряженности магнитного поля H в пространстве вне сверхпроводников (т.к. поле внутрь мейсснеровского сверхпроводника проникает лишь на
очень малую глубину), если сверхпроводниковая система находится в постоян-
ном внешнем магнитном поле H e , а в сверхпроводниковых элементах протекают полные замкнутые токи Ii .

27
В случае, когда все сверхпроводниковые элементы – односвязные тела
|
|
|
|
|
|
|
|
|
|
(Ii = 0), скалярный магнитный потенциал |
, определенный как |
H = – grad , |
|||||||
удовлетворяет уравнению Лапласа в области |
: |
|
|
||||||
2 |
= 0 |
|
|
(60) |
|||||
|
|
|
|
|
|
|
|
||
и граничным условиям |
|
|
|
|
|||||
|
|
|
|
|
|
0 , |
|
|
(61) |
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|||
|
|
|
|
S |
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
n H e , |
|
(62) |
|
|
n |
S |
|
||||||
|
|
|
|
|
|||||
где S – поверхность сверхпроводника, S – любая удаленная поверхность, где |
|||||||||
можно не учитывать влияние сверхпроводников на распределение поля, |
|
||||||||
n – |
|||||||||
внешняя нормаль к этой поверхности.
Если в двусвязном сверхпроводнике (кольце) течет полный замкнутый ток I, то скалярный магнитный потенциал обладает свойством неоднозначности: он изменяется на I при обходе по любому замкнутому пути, охватывающему сверхпроводник с током. Поэтому требуется определить некоторую поверх-
ность разреза, где потенциал меняется скачкообразно: |
|
+ – – = I, |
(63) |
где + и – – значения потенциала в одной и той же точке на двух сторонах поверхности. Если известен ток I , то (63) является достаточным условием формулировки задачи. Однако при изменении внешнего поля и тока, а также при любом изменении формы кольца и его перемещении в пространстве, необходимо учитывать важное свойство сверхпроводников, согласно которому полный магнитный поток через кольцо остается постоянным:
|
|
|
|
|
|
HdS |
|
dS LI |
e const |
0 , |
(64) |
|
|||||
|
n |
|
|
|
|
где L – индуктивность кольца, Фе – поток от внешнего поля, LI – собственный поток.
Приведенная формулировка непосредственно обобщается на случай сверхпроводниковых тел любой степени связности. При этом должны быть заданы либо токи Ii = 0, либо потоки Ф0i = 0.
Полная свободная энергия системы определяется следующим образом
W |
0 |
( ) |
2 |
d |
1 |
|
Lij Ii I j |
i Ii , |
(65) |
|
|
||||||||
2 |
|
2 |
|
||||||
|
|
|
|
i |
j |
i |
|
где Lii – коэффициент самоиндукции (индуктивность) i-го сверхпроводника, Lij (i j) – коэффициент взаимной индукции сверхпроводников, Ii – ток в i-м сверхпроводнике, Фi – собственный поток i-го сверхпроводника. Сила и момент сил

28
относительно центра О, действующие на сверхпроводниковое тело со стороны магнитного поля, определяются соответственно с помощью интегралов
|
|
0 |
|
|
2 |
|
|
0 |
|
|
2 |
|
|
|
|
|
F |
|
|
( |
) |
|
n dS , |
M |
|
|
( ) |
|
[r |
n]dS , |
(66) |
|
2 |
|
2 S |
|
|||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь интегрирование производится по поверхности сверхпроводника S , n – |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– радиус- |
внешняя нормаль к площадке dS на поверхности сверхпроводника, r |
|||||||||||||||
вектор, |
проведенный из точки О к dS. |
|
|
|
|
|
|
|
|
||||||
3.2. Д и с к р е т и з а ц и я м а т е м а т и ч е с к и х |
м о д е л е й С Э М П м е т о - |
||||||||||||||
д о м к о н е ч н ы х э л е м е н т о в |
|
|
|
|
|
|
|
|
|||||||
Согласно МКЭ, производится дискретизация геометрии области |
, такая, |
||||||||||||||
что e |
e = , e Гe – |
e Гe = Г, где |
e – подобласть, или конечный элемент, с гра- |
||||||||||||
ницей Гe . На каждой такой подобласти неизвестная функция аппроксимируется суммой
e ~ e |
(e) |
(e) |
|
(67) |
|
i |
t Ni |
r , |
i
где Ni(e) – базисные функции, или функции формы элемента е; вне элемента е
они тождественно равны нулю; (ie)(t) – параметры дискретизации – обычно значения функции в i-й геометрической точке (узле) элемента е. В такой аппроксимации при применении к (56-59) проекционного метода (Галеркина) получим систему M уравнений (M – полное число узлов или параметров)
|
M |
|
|
|
Sij |
|
i |
1 |
где |
Sij |
Sij( e) |
|
e |
|
Pij  Pij( e)
Pij( e)
e
Fj 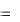 Fj(e) e
Fj(e) e
ddti Pij i
, |
Sij(e) |
, |
Pij(e) |
, |
Fj(e) |
Fj , |
j |
1, ... , M , |
|
(68) |
Ni(e) N (je)d |
, |
|
(69) |
|
e |
|
|
|
|
Ni(e) |
N (je)d |
Ni(e) N (je)d , |
(70) |
|
e |
|
e |
2 |
|
f N (je)d |
|
qN (je)d |
. |
(71) |
e |
|
e 2 |
|
|
Здесь в суммировании по элементам е принимают участие только элементы, имеющие общие узлы i и j. Важно отметить, что матрицы [S], [P] имеют разреженный вид, т. е. много нулей вне главной диагонали, а также – при гладких монотонных функциях , – диагональное преобладание.
Интегрирование уравнения (68) по времени проводится по неявной двуслойной схеме Кранка–Николсона. Решение нелинейной системы на каждом временном слое организуется с помощью метода Ньютона–Рафсона. Приводятся вычислительные схемы, как для общего, так и для частных случаев задачи

29
(56-59), а также способы учета граничных условий на границе раздела сред, неоднородных условий Дирихле, Неймана и других дополнительных условий.
Решение задачи, определяемой уравнениями (60-62), для односвязной сверхпроводниковой магнитной системы во внешнем однородном поле методом конечных элементов сводится к системе
Hij i Gi , i, j 1, ... , M , |
(72) |
i
где матричные элементы Hij вычисляются по формуле
Hij  Hij(e) , Hij(e) Ni(e) N (je)d , (73)
Hij(e) , Hij(e) Ni(e) N (je)d , (73)
e |
e |
|
а компоненты вектора правых частей Gi определяются из учета граничных условий Дирихле и Неймана и условий скачка.
Задача усложняется в случае необходимости выполнения условия сохранения потока Фi0 через отверстие каждого двусвязного сверхпроводника (уравнения (64)). Теперь токи Ii как неизвестные величины должны быть включены в левую часть системы (72). Для этого при учете условия скачка члены, содержащие Ii , оставляем в левой части уравнений. В итоге получим систему вида
Sij i Dm I m Gi , m = 1, ... , n 1
i
(Dm – некоторые коэффициенты из {Sij}), включающую M уравнений при M+n–1 неизвестных (M – число узловых переменных, n – степень связности области). Недостающие уравнения получим путем дискретизации (64):
|
|
|
Yim i |
|
|
|
0m , |
m |
1,..., n 1, |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
N (e) d |
|
|
|
||
|
|
Y (e) , |
Y (e) |
|
|
|
n , если элементe S |
|
; |
||
|
|
|
|
|
|
||||||
где |
Y |
2 |
|
Sm |
i |
|
m |
|
|||
|
im |
im |
im |
|
|
|
|
|
|
|
|
|
|
e |
|
0, |
|
|
в противном случае. |
||||
|
|
|
|
|
|
||||||
Коэффициент 1/2 здесь определяется тем, что берутся элементы по обе стороны от Sm .Очевидно, полученная система уравнений не является симметричной, а матрица этой системы в общем случае не положительно определенная. Данное обстоятельство создает повышенные требования к устойчивости вычислительного процесса.
30
3.3. Описание программного комплекса системы компьютерного моделирования
На основе описанных выше математических моделей создана система компьютерного моделирования (СКМ) процессов в криогенных гравиинерциальных приборах, основанная на методе конечных элементов (МКЭ). Система включает в себя несколько относительно самостоятельных блоков, согласованных по типу и структуре данных, которые в интерактивном режиме реализуют основные этапы решения конечноэлементной задачи (рис. 7):
*препроцессор – описание геометрии объекта и его свойств, генерация се-
ти;
*процессор (решатель) – формирование и решение системы дискретных уравнений;
*постпроцессор – визуализация и обработка результатов; получение производных характеристик.
Всистему также входит база данных предметной области, библиотеки характеристик и свойств объектов, типичных геометрических конфигураций, типов конечных элементов и др. Управление системой осуществляется из общего меню, основные программы реализованы в виде интегрированной среды и обеспечивают высокую степень визуализации данных и результатов. Примерная последовательность действий при решении конечноэлементной задачи показана на рис. 8.
