
Физико-математическое моделирование криогенных гравиинерциальных устройств. Шунин Г.Е., Кострюков С.А
.pdf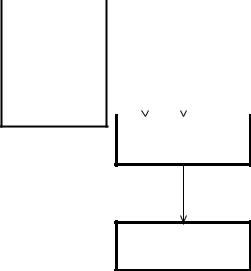
61
ПРИЛОЖЕНИЕ
Лабораторная работа № 1.
ЗНАКОМСТВО С ПАКЕТОМ ПРОГРАММ ПО КОНЕЧНО-ЭЛЕМЕНТНОМУ АНАЛИЗУ. ОСНОВНЫЕ ФУНКЦИИ ПРЕ – И ПОСТПРОЦЕССОРА
Структура пакета
Пакет представляет собой совокупность программ, которые могут функционировать независимо друг от друга, а будучи объединенными позволяют решить задачу или систему задач при рассмотрении одного или нескольких заданных объектов. Пакет состоит из следующих основных блоков:
1)препроцессор (задание входных данных задачи, дискретизация области);
2)процессор (реализация конечно-элементных вычислений);
3)постпроцессор (обработка и анализ результатов).
Кроме того, существуют вспомогательные и сервисные программы, обеспечивающие взаимодействие и эффективную работу перечисленных блоков, а также управление памятью компьютера.
Обмен данными между программными еди- |
|
|
|
|
|
|
ницами осуществляется в виде файлов. В любой мо- |
|
|
Препроцессор |
|
||
мент функционирования программ пре- и постпроцес- |
|
|
|
pre2d.exe |
|
|
сора возможна визуализация объекта, конечноэле- |
|
|
|
|
||
Указание |
|
|||||
ментной сетки, изменения масштаба и ракурса изо- |
|
|
Файлы: |
|||
параметров |
|
|
||||
бражения. Вся информация о геометрии, граничных |
|
|
taskinfo.xxx |
|||
задачи и |
|
|
|
|||
условиях, физических свойствах задачи сохраняется в |
|
|
xr____.xxx |
|||
виде отдельного файла (taskinfo.xxx). Выполнение |
режима |
|
|
yr____.xxx |
||
задачи может быть возобновлено на любом этапе без |
вычисления |
|
|
nn1___.xxx |
||
дополнительного ввода данных. Достаточно просто |
|
|
potent_.xxx |
|||
appl_fem.exe |
|
|
||||
производится корректирование исходных данных. |
|
|
|
|
||
Процессор
dft.exe
файлрешение: rhs___.xxx
Постпроцессор
post2d.exe
Рис. 27.
Команды препроцессора
1) Препроцессор (программа pre2d.exe) обеспечивает задание геометрии исследуемого объекта, триангуляцию (разбиение на конечные элементы) области, задание физических свойств и иных условий.
Моделирование геометрии области производится с помощью вспомогательных узлов, линий и зон. Узлы вводятся с клавиатуры заданием их координат. Линии могут быть прямыми (проводятся по двум узлам) и кривыми (проводятся по 3 – 4 узлам). Зона задается с помощью уже введенных линий. Вспомогательным узлам, линиям и зонам присваивается соответствующий номер, который отображается на экране дисплея. Геометрические преобразования (вращение, зеркальное отображение, сдвиг, гомотетия и т. п.) облегчают построение сложных объектов с повторяющимися структурами.
Используется два способа дискретизации геометрии. Первый предназначен для четырехугольных зон, при разбиении которых задаются числа деления на двух смежных сторонах; на противоположных им сторонах числа деления считаются теми же самыми. Второй способ использует метод Делоне [10] и пригоден для многоугольных зон. Для задания четырехугольной зоны следует вводить только номера противолежащих линий (два числа), для задания же зоны Делоне вводятся все линии, образующие зону, по часовой стрелке или против.
Впроцессе разбиения следует придерживаться следующих правил:
–линии должны проходить по физическим границам области, а также произвольным образом внутри области, обеспечивая ее дробление на зоны;
–линии, образующие зону, не должны слишком различаться по длине (максимальное допустимое отношение длин – 2–3);
–зоны должны иметь форму, близкую к выпуклой;
62
– необходимо следить за тем, чтобы конечные элементы имели форму, не слишком сильно отличающуюся от правильной (допускается отношение r/R , где r – радиус вписанной в треугольник окружности , R – радиус описанной окружности, от 0,5 до 0,1).
Все функции препроцессора могут быть вызваны через основное меню, расположенное вверху экрана. Вход в него осуществляется с помощью клавиши “F10”. Некоторые часто используемые функции (например, ввод узлов, линий и т. п.) продублированы “горячими” клавишами. Ниже перечислены основные операции и команды препроцессора. Сведения по дополнительным функциям и возможностям можно найти в меню “Help”
(или “Alt+H”).
Ввод узлов. Для ввода вспомогательных узлов нужно войти в основное меню (“F10”), выбрать пункт “Ввести”, в появившемся подменю выбрать “Узлы”, и в строке ввода внизу экрана ввести координаты узлов согласно шаблону. Тот же эффект даст нажатие клавиши “F3”. Одновременно можно задать координаты нескольких узлов.
Ввод линий. Для ввода линии нужно войти в основное меню (“F10”), выбрать пункт “Ввести”, в появившемся подменю выбрать “Линии”, а затем выбрать нужный вам вид линии в списке. Тот же результат дает нажатие “F4”. Далее в подменю выбирается способ задания линии и в строке ввода вводятся численные данные согласно шаблону. Например, чтобы соединить узлы 2 и 5 прямой линией (рис. 29), нужно выбрать пункт “Прямая по узлам” и ввести номера узлов (2,5).
Ввод зон. Для ввода зон можно воспользоваться как основным меню (“Ввести”, “Зона четырехугольная” или “Зона Делоне”), либо “горячими” клавишами: “F5” для обычной, “Alt+F5” для зоны Делоне. Затем в строке ввода указываются для обычной зоны номера двух противоположных линий, а для зоны Делоне список всех линий, образующих зону. Например, для ввода зоны 1 обычного типа (рис. 30) нужно задать номера линий (1, 6), либо (3, 4).
Ввод граничных условий. На линиях, являющихся границами расчетной области, могут быть введены граничные условия Дирихле, Неймана или смешанные. Для этого можно воспользоваться либо основным меню (“Ввести”, “Граничные условия”), либо клавишей “F7”. На экране линии, где заданы граничные условия, будут жирными.
5 |
|
|
|
|
6 |
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
4 |
|
|
7 |
|
|
|
Рис. 28. |
|
|
||
5 |
|
|
|
6 |
6 |
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
7 |
|
|
5 |
3 |
|
6 |
|
6 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
1 |
3 |
4 |
1 |
5 |
7 |
|
|
|
|
|
4 |
|
|
|
2 |
1Рис. 29. |
|
7 |
||
|
|
3 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
1 |
|
4 |
|
5 |
7 |
|
|
|
|
Рис. 30. |
|
|
Удаление объектов. Для удаления каких-либо объектов (узлов, линий, зон, конечноэлементной сетки внутри отдельной зоны, граничных условий и др.) можно воспользоваться как основным меню (“Удал”), либо клави-
шей “Delete”.
Изменить масштаб изображения, перерисовать. Для изменения масштаба изображения или сдвига области просмотра можно воспользоваться основным меню (“Масшт”) или клавишей “F1”. Размер рамки, изображение внутри которой будет растянуто на весь экран, изменяется клавишами “<”, “>”, а перемещается она с помощью стрелок.
Разрешить/запретить вывод номеров объектов. Чтобы не загромождать изображение, можно запретить или разрешить вывод на экран номеров объектов. Для этого нужно воспользоваться основным меню (пункт “Опции”).
Разбить зону на конечные элементы. Разбить зону можно либо через основное меню (“Разб”), либо нажав “F8”. Если вы разбиваете первую по счету зону, программа предложит ввести тип КЭ. Затем вы должны будете задать числа деления на тех линиях, где они еще не определены. Для разбиения зоны, введеной как четырехугольная, методом Делоне следует вместо “F8” нажать “Alt+F8”.
Операции. Для облегчения построения сложных областей с повторяющимися структурами в программе предусмотрены некоторые операции (сдвиг, параллельный перенос, поворот, зеркальное отображение). Они
5 |
|
6 |
6 |
|
3 |
4 |
|
|
|
|
|
2 |
1 |
|
7 |
|
3 |
|
|
|
2 |
|
|
1 |
4 |
5 |
7 |
|
|
Рис. 31. |
|
63
вызываются через основное меню (пункт “Опер”), либо горячей клавишей “Space” Объектами этих операций могут быть узлы, линии и зоны.
Сохранить задачу. Записать введенную геометрию и разбиение можно с помощью основного меню (“Задача”, “Сохранить задачу”), или нажав “F2”.
Загрузить задачу. Записанную на диск задачу можно загрузить с помощью основного меню (“Задача”, “Загрузить задачу”), или нажав “F9”.
Директивы процессору
2) Процессор (программа dft.exe) осуществляет все конечноэлементные вычисления (формирование системы алгебраических уравнений и ее решение).
Входные данные – массивы, полученные препроцессором. Указания по режиму вычислений, информация о типе и параметрах задачи содержится в файле taskinfo.xxx. На выходе процессор выдает значения искомых величин в каждом узле сети. В связи с большой разреженностью матрица системы уравнений хранится в виде графа. Нулевые элементы не хранятся.
Основные этапы вычислений:
а) формирование структуры хранения матрицы; б) построение подматриц и подвекторов на каждом конечном элементе;
в) объединение этих подматриц и подвекторов для формирования глобальной матрицы и вектора правых частей;
г) учет граничных условий; д) решение системы линейных алгебраических уравнений.
В случае нелинейной задачи осуществляется итерационный процесс по методу Ньютона. Если задача к тому же и нестационарна, производится пересчет на каждом временнóм отсчете .
Команды постпроцессора
Постпроцессор (программа post2d.exe) позволяет проанализировать полученное решение задачи и представить результаты в наглядной форме. Имеется возможность вывести на экран эквипотенциальные кривые с любым шагом, конечноэлементную сеть, построить графики изменения искомой величины и ее градиента вдоль любой линии внутри расчетной области или на ее границе. Изображение на экране в любой момент можно вывести на принтер.
Вывод эквипотенциальных кривых – “F3”. По запросу следует ввести шаг (интервал), с которым будут выводиться эквипотенциали.
Разрешить/запретить вывод конечноэлементной сетки – “F2”. Для остановки процесса рисования сетки на-
жмите любую клавишу.
График искомой величины или ее градиента – “G”, “Alt+G”, “Ctrl+G”. В одном случае отрезок, на котором сто-
ится график, задается координатами его начала и конца, в другом – номерами вспомогательных узлов, введенных в препроцессоре (эти узлы можно отобразить с помощью “Alt+P”). В третьем случае вычисление требуемой величины осуществляется вдоль одной или нескольких вспомогательных линий, которые отображаются комбинацией клавиш “Alt+L”.
Печать таблицы значений искомой величины и ее градиента – “Alt+F4”. По запросу следует задать начало и ко-
нец интервала и число точек на этом интервале.
Вывести содержимое экрана на принтер –“F4”.По запросу следует выбрать положение выводимого изображения на листе (вертикальное или горизонтальное). Подразумевается, что принтер Epson-совместимый, он включен и что в нем есть бумага.
Помимо перечисленных, имеется еще ряд функций, например:
Закраска области в зависимости от значений искомой величины. Вывод матрицы стрелок.
Трехмерный график функции.
Вычислить (энергию, силу, момент сил, максимальный градиент потенциала, и т.д.)…
Пример. Методом конечных элементов найти стационарное распределение температуры в приведенном на рис. 32 секторе круга. Использовать показанные краевые условия.

|
|
|
|
|
|
64 |
|
|
|
|
|
|
Этот процесс описывает стационарное уравнение |
|
y |
|
|
|
|||||||
теплопроводности при отсутствии источников тепла |
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
––– = –2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
x 2 |
y 2 |
|
|
|
|
––– = 0 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
с краевыми условиями типа Дирихле и Неймана. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
= 0 |
1 |
x |
|
|
|
|
|
|
|
|
|
|
Рис. 32. |
|
|
Дискретизация этого уравнения на основе вариационного метода и метода проекций рассмотрена в |
||||||||||||
разд. 2.4. (если положить = 1, |
= 0). В приведенной формулировке краевое |
|
|
|
|
|||||||
условие Неймана играет роль естественного условия, а условие Дирихле – |
|
|
|
|
||||||||
главного. |
|
|
|
|
|
|
|
|
2 |
|
|
|
Порядок действий на ЭВМ: |
|
|
|
|
|
|
|
|
|
|||
1) запустить программу-препроцессор pre2d.exe; |
|
|
|
|
|
|
|
|||||
2) ввести номер задачи (от 1 до 999); |
|
|
|
|
|
|
|
|
|
|
||
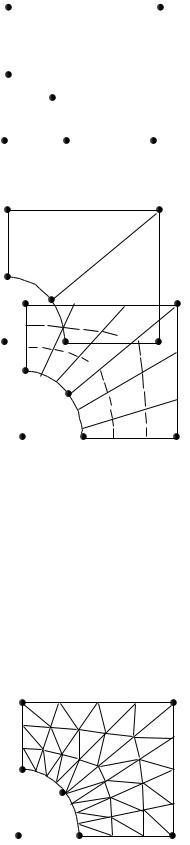
3) с помощью “F3” ввести координаты точек (0, 0), (0, 1), (1, 0) (рис. 33); |
|
|
|
|
||||||||
4) с помощью “F4” ввести три линии, ограничивающие область: две пря- |
1 |
|
3 |
|
||||||||
мых (1–2) и (1–3) и дугу окружности (2–3) (рис. 34); |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
5) с помощью “Alt+F5” ввести зону Делоне, задав номера трех введенных |
|
Рис. 33. |
|
|||||||||
линий; |
|
|
|
|
|
|
|
|
2 |
|
||
6) с помощью подменю «Гр. Условия» ввести на соответствующих линиях |
|
|
|
|||||||||
зоны граничные условия; |
|
|
|
|
|
|
|
1 |
|
3 |
|
|
7) с помощью “F8” разбить зону на конечные элементы методом Делоне. |
|
|
||||||||||
По запросу ввести числа деления вдоль каждой стороны зоны (рис. 35); |
|
|
|
|
|
|||||||
8) с помощью “F2” записать данные на диск; |
|
|
|
|
|
|
|
|
||||
9) выйти из препроцессора (“Alt+X”); |
|
|
|
|
|
1 |
2 |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
10) запустить программу-процессор femtsk.exe; |
|
|
|
2 |
|
|
|
|||||
11) запустить постпроцессор post2d.exe и проанализиро- |
1 Рис. 34.3 |
|
||||||||||
вать результаты, например, вывести эквипотенциальные кривые |
|
|||||||||||
|
1 |
|
|
|||||||||
с помощью “F3”. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
Лабораторная работа №2 |
|
|
1 |
2 |
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
РЕШЕНИЕ |
КРАЕВЫХ |
ЗАДАЧ |
ДЛЯ |
ОБЫКНОВЕННЫХ |
|
Рис. 35. |
|
|||||
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
РАСПРЕДЕЛЕНИЕ ТЕПЛА В ТОНКОМ ОДНОРОДНОМ |
|
|
|
|
||||||||
|
|
|
|
|
СТЕРЖНЕ |
|
|
|
|
|
||
Теоретические сведения. Обыкновенными дифференциальными уравнениями называются такие урав- |
||||||||||||
нения, которые содержат одну или несколько производных от искомой функции |
= (x). Их можно записать в |
|||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
x, |
, |
d |
, ... , |
d n |
0 , |
|
|
|
|
|
|
dx |
dx n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
где x – независимая переменная. |
|
|
|
|
|
|
|
|
|
|
|
|
Общее решение обыкновенного дифференциального уравнения n-го порядка содержит n произвольных |
||||||||||||
постоянных C1, C2, ... , Cn , т. е. имеет вид |
|
|
|
|
|
|
|
|
|
|||
= (x, C1, C2, ... , Cn ).
Частное решение обыкновенного дифференциального уравнения получается из общего, если произвольным постоянным придать определенные значения. В зависимости от способа задания дополнительных условий для получения частного решения дифференциального уравнения существуют два различных типа задач: задача Коши и краевая задача. Если эти условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями, а точка x = x0 , в которой
они задаются, – начальной точкой. Если же дополнительные условия задаются в более чем одной точке, т. е. при разных значениях независимой переменной, то такая задача называется краевой. На практике обычно гра-

65
ничные условия задаются в двух точках x = a и x = b, являющихся границами области решения дифференциального уравнения.
Для решения краевых задач обычно используются методы конечных разностей и конечных элементов. Задачи Коши чаще всего решаются методами Эйлера, Рунге–Кутта, Адамса и т. п.
|
Пример. Решить методом конечных элементов уравнение |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d 2 |
|
|
|
|
e x |
0, 0 x |
L |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
при условии, что |
= 0 при x = 0 и / |
|
x = 0 при x = Lx. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Упражнения |
|
|
|
||||||
1. Задано дифференциальное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
p(x) |
du |
|
q(x)u f (x) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
dx |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
на интервале [a, b]. Требуется найти функцию u(x) такую, что u(a) = d0 , u(b) = d1. |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
|
|
a |
|
|
B |
|
|
|
d0 |
|
|
|
|
|
d1 |
|
p(x) |
q(x) |
f(x) |
||||
|
варианта |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
–1 |
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
sin x |
–(1+x2) |
e x |
|||
|
2 |
|
|
0 |
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
–2 |
|
1 |
0 |
–2 |
|||
|
3 |
|
|
0 |
|
|
10 |
|
|
|
|
0 |
|
|
|
|
|
10 |
|
1 |
0 |
0 |
|||
|
4 |
|
|
0 |
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
1 |
|
1 |
0 |
–sin x |
|||
|
5 |
|
|
1 |
|
|
3 |
|
|
|
|
|
–1 |
|
|
|
|
|
1 |
|
1 |
0 |
– e x |
||
|
6 |
|
|
–1 |
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
0 |
|
1 |
0 |
–x |
|||
|
7 |
|
|
0 |
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
3 |
|
sin x |
–4 |
cos x |
|||
|
8 |
|
|
0 |
|
|
1 |
|
|
|
|
|
–1 |
|
|
|
|
|
–1 |
|
e x |
–2 |
x |
||
|
9 |
|
|
–1 |
|
|
0 |
|
|
|
|
|
–1 |
|
|
|
|
|
2 |
|
2x |
–(1+x2) |
2 |
||
|
10 |
|
|
4 |
|
|
5 |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
– e x |
–6 |
sin x |
|||
2. Для нелинейного дифференциального уравнения |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
d |
|
( ) |
d |
|
|
|
|
f (x, ) , |
0 x 1 |
|
|
||||||
|
|
|
|
|
|
|
|
dx |
dx |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
с краевыми условиями |
(0) = 0, |
(1) = 1 |
|
провести дискретизацию и получить численное решение |
|||||||||||||||||||||
1) = ; f = –2; |
|
|
|
|
|
|
|
|
|
|
4) = e ; f = x; |
|
|
|
|||||||||||
2) |
= cos( |
/2); f = 0; |
|
|
|
|
|
|
|
|
5) |
=1+ 0.1 ; |
f = –10x; |
|
|
|
|||||||||
3) |
=1/( |
+1); f = 0; |
|
|
|
|
|
|
|
|
6) |
=1; |
|
f = e |
; |
|
|
|
|
||||||
3. Решить уравнение d 2 |
/d 2x + |
|
= x , 0 |
|
x 1 с краевыми условиями: |
|
|
|
|||||||||||||||||
1) |
= 0 при x=0 и |
=0 при x=1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2) = 0 при x=0 и d /dx=0 при x=1;
3)= 0 при x=0 и d /dx+ =0 при x=1.
Провести дискретизацию на основе вариационного метода.
4. Решить уравнение d 2 /d 2x – |
= 0 , 0 x 1 с краевыми условиями = 0 при x=0 и d /dx=20 при x=1. |
Лабораторная работа №3

66
РЕШЕНИЕ ДВУМЕРНЫХ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
(СТАЦИОНАРНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ)
Теоретические сведения. Во многих практических задачах искомые функции зависят от нескольких переменных, и описывающие такие задачи уравнения могут содержать частные производные искомых функций. Они называются дифференциальными уравнениями с частными производными (ДУЧП).
Полная математическая постановка задачи наряду с ДУЧП содержит также некоторые дополнительные условия. Если решение ищется в ограниченной области, то задаются условия на границе, называемые граничными (краевыми) условиями. Такие задачи называются краевыми задачами для ДУЧП. Если одной из независимых переменных в задаче является время t, то задаются некоторые условия (например, значение искомой функции) в начальный момент t0, которые называются начальными условиями. Такая задача называется задачей Коши для ДУЧП. При этом задача решается в неограниченном пространстве и граничные условия не задаются. Задачи, при формулировке которых ставятся и граничные, и начальные условия, называются нестационарными (или смешанными) краевыми задачами
Задача называется корректной поставленной (по Адамару), если ее решение существует, единственно и непрерывно зависит от начальных и граничных условий, от коэффициентов и правой части дифференциального уравнения.
Рассмотрим узкий класс корректных задач для уравнений 2-го порядка, линейных относительно произ-
водных. В случае четырех независимых переменных v1 |
x, v2 |
y, v3 |
z, v4 |
t эти уравнения можно запи- |
||||
сать в виде |
|
|
|
|
|
|
|
|
4 |
|
2 |
|
4 |
|
|
|
|
aij |
|
|
|
bi |
|
c |
f . |
(97) |
|
vi v j |
|
||||||
i, j 1 |
i 1 |
vi |
|
|
||||
Здесь = (x, y, z, t) – искомая функция. Коэффициенты {aij},{bi} и правая часть f, вообще говоря, могут зависеть от {vi} и . В связи с этим уравнение может быть а) с постоянными коэффициентами, б) линейным, если f линейно зависит от , а коэффициенты – только от {vi}. Если f=0, то уравнение называется однородным.
Можно показать, что путем замены vi= ijwj, подобрав соответствующим образом |
ij, можно (97) привес- |
|||||||||
ти к виду, в котором не будет смешанных производных |
|
|
|
|
|
|
|
|
||
|
4 |
|
2 |
4 |
~ |
|
|
|
|
|
|
|
|
|
|
bi |
|
|
c |
f . |
(98) |
|
i |
wi2 |
|
wi |
||||||
|
i 1 |
i 1 |
|
|
|
|
||||
Если ни один из коэффициентов |
i не равен 0 и все они одного знака, то уравнение (98) называется эллиптиче- |
|||||||||
ским. Если среди коэффициентов |
i хотя бы один равен 0 (но не все одновременно), то уравнение является пара- |
|||||||||
болическим. Гиперболическое уравнение соответствует случаю, когда все i |
0 и разных знаков. |
|||||||||
Эллиптические уравнения описывают стационарные (установившиеся) процессы во многих физических приложениях (распределение тепла, электростатических и магнитостатических полей, безвихревое течение идеальной жидкости и др.).
Рассмотрим стационарное уравнение теплопроводности
|
|
|
k |
|
|
|
|
|
k |
|
|
|
|
k |
|
|
Q 0 , |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
x |
y |
|
y |
|
z |
|
z |
|
|
|
|
|
|
|
||||||
где k(x, y, z) – коэффициент теплопроводности, |
Q(x, y, z, t) – количество тепла, генерируемого в ед. объема, |
(x, |
|||||||||||||||||||||
y, z, t) –распределение температуры. Это уравнение дополняется начальными и краевыми условиями: |
= 0 |
при |
|||||||||||||||||||||
t = t0 ; = на |
1 и –k |
n = q на |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. Найти стационарное распределение температуры в прямоугольной пла- |
y |
|
(0, b) |
(a, b) |
|||||||||||||||||||
|
|||||||||||||||||||||||
|
|
||||||||||||||||||||||
стине размеров 0 |
x а, 0 |
y b в отсутствие источников тепла. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0, 0) |
(a, 0) x |
Номер |
а |
b |
Граничные условия |

|
|
|
|
67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
варианта |
|
|
x = 0 |
x = a |
y = 0 |
y = b |
|
|
1 |
1 |
1 |
= 0 |
––– = 1 |
= 0 |
––– = –1 |
|
|
|
|
|
|
n |
|
n |
|
|
2 |
0.8 |
1.5 |
=10 |
= 20 |
––– = 0 |
––– = 0 |
|
|
|
|
|
|
|
n |
n |
|
|
3 |
1.25 |
1 |
= 0 |
= 0 |
= 0 |
––– = 2 |
|
|
|
|
|
|
|
|
n |
|
|
4 |
2 |
1 |
= 5 |
= –5 |
––– = 0 |
––– = –2 |
|
|
|
|
|
|
|
n |
n |
|
|
5 |
0.9 |
1.6 |
––– = 1 |
––– = –1 |
= 0 |
––– = –1 |
|
|
|
|
|
n |
n |
|
n |
|
|
6 |
1 |
2 |
= –y |
––– = 2 |
––– = 0 |
––– = 0 |
|
|
|
|
|
|
n |
n |
n |
|
|
7 |
1 |
1 |
= –y |
––– = 2 |
= x |
––– = –2 |
|
|
|
|
|
|
n |
|
n |
|
|
8 |
1 |
1.5 |
= 0 |
= 1.5 |
= 0 |
|
= x |
|
9 |
1 |
0.6 |
= 0 |
= 0 |
= 0 |
––– + |
= 0 |
|
|
|
|
|
|
|
n |
|
|
10 |
1 |
1 |
––– = 0 |
––– = 0 |
= 10 |
––– + |
= 0 |
|
|
|
|
n |
n |
|
n |
|
|
2. Найти стационарное распределение температуры в прямоугольной пластине 0 |
x а, 0 y b, все стороны |
|||||||
которой поддерживаются при нулевой температуре. Пластина нагревается от источников тепла, мощность которых описывается законом Q(x,y) = c (x2 + y2) + d (c , d – постоянные).
|
Данная задача сводится к решению уравнения Пуассона k |
=–Q(x,y) (k – коэффициент теплопроводно- |
|||||||||
сти) в прямоугольнике с граничными условиями (x, 0) = (x, 1) = |
(0, y) = (1, y) = 0. |
||||||||||
3. Решить задачу распространения тепла в стенках трубы, изображенной |
|||||||||||
на рисунке. На внутренней границе поддерживается |
постоянная темпе- |
|
|
|
|
||||||
ратура |
100 С, а |
на |
внешней |
границе |
задано |
условие |
|
|
|
|
|
k ––– = – |
(для простоты положить k=1, |
=1). |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лабораторная работа №4
РЕШЕНИЕ ДВУМЕРНЫХ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА
(НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ)
1. Найти изменение распределения температуры со временем в тонком однородном стержне. На концах стерж-
ня задаются температурные режимы. Начальная температура всего стержня постоянная.
Задача сводится к решению уравнения теплопроводности

68
2
|
|
|
|
|
|
|
|
k |
|
, 0 |
t t1, 0 |
x a, |
||
|
|
|
|
|
t |
x2 |
||||||||
|
|
|
|
|
|
|||||||||
(x, 0) = 0, (0, t) = |
0(t), |
(a, t) = 1(t), где |
|
(x, t) – температура стержня в точке x в момент времени t. k при- |
||||||||||
нять равным 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
варианта |
|
а |
|
t1 |
|
0 |
|
0(t) |
|
1(t) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1.2 |
|
2 |
|
|
|
10 |
|
0 + 0.2t |
|
0 – 0.3t |
|
|
2 |
|
1.1 |
|
2.2 |
|
|
|
12 |
|
0 – t |
|
0 + sin2 t |
|
|
3 |
|
0.8 |
|
2.4 |
|
|
|
15 |
|
0 |
|
0 – 4t |
|
|
4 |
|
0.6 |
|
2.6 |
|
|
|
18 |
|
0 e t |
|
0 e –t |
|
|
5 |
|
1.4 |
|
2.8 |
|
|
|
22 |
|
0 + sin t |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Найти изменение температуры (x, y, t) во времени для однородной квадратной пластины. Начальное рас-
пределение температуры задано: |
(x, y, 0) = x + y. Краевые условия: (x, 0, t) = xe –at; (x, 1, t) = (1 + x)e –at; (0, |
|||
y, t) = ye –at; |
(1, y, t) = (1 + y)e –at. Задача сводится к решению уравнения теплопроводности |
/ t = k |
в об- |
|
ласти {0 x |
1 , 0 y 1 , 0 t |
t1}. Коэффициент k принять равным 1, t1 и a взять из таблицы к упр. 6. |
|
|
Лабораторная работа №5–6
МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ЭКРАНОВ
А . Э л е к т р о с т а т и ч е с к и е э к р а н ы
Электростатические экраны предназначены для экранирования постоянных электрических полей.
Задача формулируется следующим образом:
|
Г1 |
|
|
Ее |
Г |
|
2 |
|
|
|
|
|
|
div grad |
= 0 в области |
, (99) |
||
|
|
|
|
1 |
|
const, |
(100) |
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Ee |
n , |
(101) |
|
|
n |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
где Г1 |
– поверхность экрана; Г2 – внешняя удаленная |
|||||||||
|
|
|
|
|
|
|
|
|
||
граница; Ее – напряженность внешнего постоянного
электрического поля; Е = – grad .
Неоднородное условие Неймана (101) может быть заменено на условие Дирихле, когда внешнее поле создается системой электродов с заданными потенциалами 1, 2, ... .
Задания
Для изображенных областей и указанных граничных условий найти распределение электростатического поля, построить эквипотенциальные кривые и графики изменения напряженности поля вдоль нескольких линий. Определить коэффициент экранирования поля S =Ee/Ei (Ei – поле в центре либо в другой точке экрана).

69
Указание. При заданном внешнем поле Ee расчет произвести в двух вариантах – в продольном и попе-
речном поле с Ee 1; если явно не указаны границы расчетной области, то последнюю следует выбирать в
виде прямоугольника со сторонами, равными пяти-шести характерным размерам экрана. Если специально не
указаны граничные условия, определяющие внешнее поле Ee , то задать их можно двумя способами:
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
AB |
|
0 ; |
|
|
|
|
CD |
0 |
Ee |
|
|
|
|
AD |
(25а) |
|||
|
|
|
|
|
|
||||||||||||||
( 0 |
выбирается произвольно) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
||
|
|
|
|
|
|
|
|
|
|
||||||||||
2) |
|
n |
AB |
|
Ee |
|
; |
|
n |
CD |
|
|
Ee |
|
|
(25б) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=0 (в любой точке сетки)
B |
С |

Е
A D
|
|
|
|
|
I. |
Задачи с плоской геометрией |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1. Плоская пластина во внешнем |
2. Две пластины во внешнем поле |
|
|
|
|||||||||||
поле |
|
|
|
|
|
|
|
b |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ее |
|
|
Г1 |
|
а |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Ее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(отношение сторон 4 |
1, 8 1, 12 1) |
|
|
|
1 = 0 |
2 = 0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
a : b : c = 8 : 1 : 5; 6 : 1 : 2; 4 : 1 : 4 |
|||||||||
|
|
|
|
|
|
||||||||||
3. Бесконечно длинный экран |
|
|
4. Система электродов во внешнем |
|
с поперечным сечением вида: |
|
|
поле |
|
|
|
|
d |
3 |
|
|
|
|
|
b |
c |
|
|
1 |
|
Г1 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
5 |
|||
|
|
|
|
|
||||
a:b = 3:2; 2:1; 1:1; |
|
|
|
|
|
|
||
a) Ее |
0, 1 = 2 = 3 = 4 = |
5 = 0. |
||||||
|
||||||||

|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
c:a = 1:4; 1:3: 1:2; |
|
|
|
б) |
Ее |
= 0, |
1 = |
2 = 1; |
3 = |
4 = |
5 = 0. |
||
d:a = 1:12; 1:8: 1:4 |
|
|
|
в) |
Ее |
= 0, |
1 = |
3 = |
5 = 0; |
2 = |
4 = 1. |
||
5. Заряженные проводники во |
|
|
|
|
|
|
a |
|
|
|
|||
внешнем поле |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 = 0; |
0,5; 2; 5. |
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a:b = 1:1; |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
c:a = 1:5; |
|
|
|
|
|
|
|
|
|
|
|
b |
|
d:c = 1:3; 1:5. |
|
|
|
1 = 0 |
|
|
|
|
|
|
2 = 1 |
||
|
|
|
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I I. Осесимметричные задачи |
|
|
|
|
|
||||
1. Цилиндрический экран |
|
2. Полый шар с отверстием |
|
|
|||||||||
|
r |
|
|
|
|
|
|
|
r |
|
|
|
1 = 0 |
|
|
|
|
1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Ее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ее |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
z |
3. Две полусферы во внешнем поле |
4. Кольцо П-образного сечения |
|
|||||||||||
|
r |
|
|
1 = 0 |
|
|
|
r |
|
|
|
1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ее |
|
|
|
|
|
Ее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Электростатическая линза |
|
6. Цилиндрический конденсатор с двумя кольцами |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
r |
|
|
|
|
внутри |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
= 1 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a |
|
b |
c |
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
М |
У |
А |
|
|
|
|
|
|
|
|
|
|
rК К rМ |
rУ |
z |
|
|
0,5 |
|
|
|
= 0 |
z |
||
|
|
|
|
|
|
|
|
|
|
|
|||
К = 0; |
М = –70; –40; –10; |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
У = 300; 800; 1500; |
А = 6000. |
|
1) кольца проводящие ( |
=const) |
|
||||||||
rК = 0.2 мм; rМ = rУ = 0.25 мм; |
|
2) кольца из диэлектрика ( |
1) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
a = 0.15 мм; b = 0.265 мм, с = 1.22 мм. |
|
|
|
|
|
|
|
|
|
||||
Толщина электродов М и У – 0.13 и 0.52 мм соот- |
|
|
|
|
|
|
|
|
|
||||
ветственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
