Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2780

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.28 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

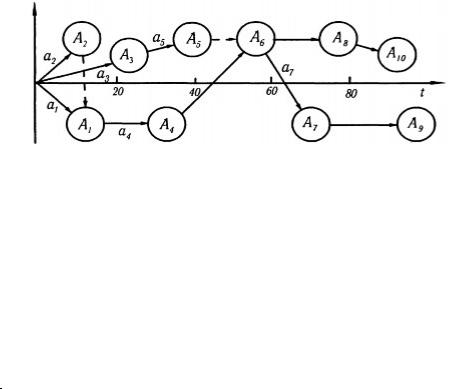
Время окончания работы равно максимальному времени окончания T = 84 и a9 последняя критическая работа.

Поскольку a9 опирается на a7 , то следующая критическая работа a7 . Так как большая работа, на которую опирается a7

будет a6 , то a6 следующая критическая работа, a6 - опирается

на a4 , а a4 - на a1 . Таким образом, a1 , a4 , a6 , a7 , a9 - критические работы. Сетевой график показан на рис. 1.1.

Рис. 1.1

1.2.Комплекс работ задан структурно-временной таблицей

Работа	Опирается	Время	Работа	Опирается	Время
ai	на работу	ti	ai	на работу	ti
a1	-	20	a5	a1 ,a2 ,a3	10
a2	-	10	a6	a1 ,a2 ,a3	5
a2	-	10	a6	a1 ,a2 ,a3	5
a3	-	8	a7	a6	5
a3	-	8	a7	a6	5
a4	a1 ,a2	20	a8	a4 ,a5 ,a7	10

Находим время выполнения работ: Т1 = 20 ; Т 2 = 10 ;

Т 3 = 8 ; Т 4 = Т1 + t4 = 40 ; T5 = T1 + t5 = 30 ; T6 = T1 + t6 = 25 ;

T7 = T6 + t7 = 30 ; T8 = T4 + t8 = 50.

101

Критические

работы будут a1 ,

a4 , a8 . Время

окончания

комплекса работ равно Т = Т1 + Т 4

+ Т8 = 50.

Уменьшим это время до Т 0

= 40 . Известно, что в работу ai

можно вложить xi

в размере не более чем сi , т.е.

при этом

xi £ ci ,

(1)

ti¢ = ti (1 - bi xi ).

(2)

Пусть для критических работ параметры будут

b1 = 0,2; b4

= 0,3;

b8 = 0,1;

c1 = 2;

c4 = 2; c8 = 5.

Условия (1) примут вид:

x1 - 2 £ 0; x4 - 2 £ 0; x5

- 5 £ 0.

(3)

Новый срок выполнения работ находим по формуле (2)

T ¢ = t1¢ + t4¢ + t8¢ = t1 (1 - 0,2x1 ) + t4 (1 - 0,3x4 ) + t8 (1 - 0,1x8 ) =

= 50 - 4x1 - 6x4 - x8 .

Поскольку

Т 0

= 40 , то 50 - 4x1 - 6x4 - x8

=£ 40, откуда

4x1 + 6x4 + x8

³ 10.

(4)

Требуется

найти

минимум

функцииL =x1 +x4

+ x8

при

неравенствах

ограничений (3),

(4),

т.е.

налицо

задача

линейного программирования.

Решая задачу симплекс методом, находим, что Lmin = 5 / 3 и

оптимальным решением будет вложение x4 = 5 / 3 в работу a4 .

2. Оптимизация размещения узлов почтовой

связи

1°.

При

проектировании

городской

почтовой

связи

необходимо

решить,

где

разместить

узлы

связи и

как

организовать

их

транспортные

связи

опорными

пунктами

102

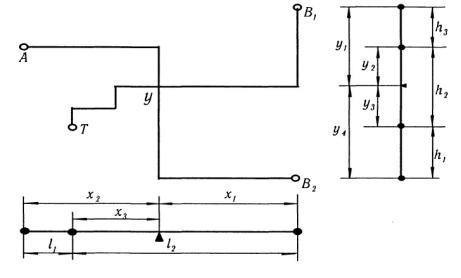
города (вокзалами, аэропортами, пристанями, типографиями и т.д.).

Пусть в городе имеется узел связи (У), два вокзала ( В1 , В2 ),

типография (Т) и аэропорт (А) (рис.1.2).
В качестве критерия оптимизации	выберем	минимум
пробега транспорта между узлом и	опорным	. пунктом
Обозначим за N1 - число рейсов за сутки между каждым из
вокзалов и узлом; N 2 - между аэропортом	и узлом; N 3 -
между узлом и типографией.

				Рис 1.2
2°.	Пусть		транспортные			магистралиобразуют
прямоугольную			сеть. Протяженность			каждого	маршрута
представим как сумму расстояний по оси x и по оси y.
Обозначим		через x1		расстояния		по горизонтали между
каждым из вокзалов и узлом; x2					- между аэропортом и узлом;
x3 - между		типографией		и	узлом. Величины l1 и		l2 заданы.
					103

Целевая функция, минимум которой требуется найти, будет

иметь вид

L1 = 2N1 x1 + N 2 x2 + N3 x3 .

Система ограничивающих условий будет

x1 + x2 ³ l1 + l2 ; x1 + x3 ³ l2 ; x2 + x3 ³ l1.

Полученная модель является моделью задачи линейного

программирования.

через y1 -

Рассмотрим по осиy. Обозначим

расстояние

между вокзалом 1 и узлом;

y2 - между аэропортом и узлом;

y3 -

между

типографией

узлом; y4

- между вокзалом 2 и

узлом. Целевая функция, минимум которой необходимо найти,

будет

L2 = N1 ( y1 + y4 ) + N 2 y2

+ N3 y3 .

Система

ограничивающих

условий, при

заданных

величинах h1 , h2 , h3 , имеет вид

y1 + y2 ³ h2 + h3 ; y2 + y3 ³ h2 ; y1 + y4 ³ h1 + h2 + h3 ;

y2 + y4 ³ h1 + h2 .

Поставленная

задача

решается

симплекс-методом. В

результате

решения

двух

задач

определяется

общ

минимальная величина пробега L = L1 + L2 ,

а соответствующее

значение переменных xi , yi

определят координаты узла.

2.1. Пример. Пусть N1

= 10;

N 2 = 8; N3

= 6; l1

= 4 км;

l2 = 8 км; h1

= 5 км;

h2 = 6 км;

= 4 км. Найти Lmin .

Решение. Математическая модель задачи относительно x

примет вид

L1 = 20x1 + 8x2 + 6x3 ;

x1 + x2 ³ 12; x1 + x3 ³ 8;

+ x3 ³ 4.

Введем базисные переменные x4 , x5 , x6 и запишем решение в виде

L = 0 - (-20x1 - 8x2 - 6x3 ); x4 = -12 - (-x1 - x2 ); 104

	x5 = -8 - (-x1 - x3 ); x6 = -4 - (-x2 - x3 ) .
	Базисные	bi	x1	x2				x3
	переменные
	L1	0	-20	-8	-8			-6	-6
		96	-12		-8				-6
	x4	-12	-1	-1	-1			0	0
		12	1		-1				0
	x5	-8	-1	0	0			-1	-1
		-8	-1		0				-1
	x6	-4	0	-1	-1			-1	-1
		8	1		-1				-1
	Находим	разрешающий	элемент	x1 и	меняемx2				« x4 .
Заполним новую таблицу.
		bi	x1	x4				x3

	L1	96	-12	-8	-8	-6			-6
		120	-6		-8				-6

	x2	12	1	-1	-1	0			0
		12	1		-1				0

	x5	-8	-1	0	0	-1			-1
		-8	1		0				-1

	x6	8	1	-1	-1	-1			1
		0	0		-1				1

	Далее заменим x3 « x5
		bi	x1	x4					x5
	L1	144	-6	-8			-6

	x2	12	1	-1					0
	x3	8	1	0			-1

	x6	0	0	-1					1

Так как в первой строке все свободные переменные

отрицательны, то L1min = 144 при x1 = 0 , x2							= 12 ,	x3 = 8 .
Математическая			модель	относительно			оси y	запишется в
виде		L2 = 10 y1 + 8 y2 + 6 y3 +10 y4 ;
		L2 = 10 y1 + 8 y2 + 6 y3 +10 y4 ;
	y1 + y4 ³ 15; y1 + y3			³ 10;		y2 + y3 ³ 6; y2 + y4			³ 11.
Через базисные переменные
	L2 = 0 - (-10 y1 - 8 y2 - 6 y3 -10 y4 ),
	y5 = -15 - (-y1 - y4 ); y6 = -10 - (-y1 - y3 );
	y7 = -6 - (-y2 - y3 ); y8 = -11 - (- y2 - y4 ).
Составим таблицу

	bi		y1			y2	y3		y4

L2	0		-10		-8	-8	-6	4	-10
	100		-10			-8		4	-10

y5	-15		-1	-1	0	0	0	1	-1
	-5			-1		0		1	-1

y6	-10		-1	-1	0	0	-1	1	0
	10			-1		0		1	0

y7	-6		0	0	-1	-1	-1	-1	0
	-6			0		-1		-1	0

y8	-11		0	0	-1	-1	0	0	-1
	-11			0		-1		0	-1

Делаем замену y1 « y6

106

105

		bi		y6			y2			y3		y4

L2	100	150	-10	0	-8		-8	4		-6	-10
		150		0			-8			-6	-10

y5	-5	5	-1	1	0		0	1		-1	-1
		5		1			0			-1	-1

y1	10	10	-1	-1	0		0	1		1	0
		10		-1			0			1	0

y7	-6	-6	0	0	-1		-1	-1		-1	0
		-6		0			-1			-1	0

y8	-11	-6	0	1	-1		-1	0		-1	-1
		-6		1			-1			-1	-1

Еще раз заменяем y4				« y5
	bi			y6			y2			y3		y5

L2	150	186	0	0		-8	-2		-6	6		-10
		186		0			-2			6		-10
y4	5	11	1	1		0	1		-1	-1		-1
		11		1			1			-1		-1

y1	10	4	-1	-1		0	-1		1	1		0
		4		-1			-1			1		0

y7	-6	6	0	0		-1	1		-1	-1		0
		6		0			1			-1		0

y8	-6	0	1	1		-1	0		-1	1		-1
		0		1			0			1		-1

				107

Отсюда	имеем:	L = 186 при y1	= 4; y2	= 0;	y3 = 6;
y4 = 11.	Следовательно, минимум		пробега	транспорта в
горизонтальном и		вертикальном	направлениях		составляет

L = 144 +186 = 330 км.

3. Расчет оптимального числа работников на предприятии

1 °. Характерной особенностью ряда предприятий является неравномерность поступления нагрузки по часам суток, дням недели и месяцам года. В условиях постоянного штата необходимо, с одной стороны, обеспечить выполнение всей

работы,	а	с другой— обеспечить			выполнение		работы
минимальным количеством работников.
Обозначим через x j			— число работников, работающих по
j - му	графику, bi -		нагрузку	в	i - й	рабочий	день,
выраженную		в	числе	требуемых		работников; a -
							ij
коэффициент,		равный	единице,	если	по j - му графику

предусматривается работа в i - й день, и нулю, если в тот день предусматривается выходной.

Задача может быть сформулирована так: требуется найти

минимум	целевой	функцииL = x1 + x2 + ... + xn при
выполнении следующих ограничений
	a11 x1 + a12 x2	+ ... + a1n xn	³ b1 ;
	a21 x1 + a22 x2	+ ... + a2n xn	³ b2 ;

……………………………….

am1 x1 + am 2 x2 + ... + amn xn ³ bm .

2°. Для простоты вычислений рассмотрим пример четырехдневной рабочей недели с двумя выходными, исходные данные для которого приведены в таблице

108

Число			Дни недели
работников	1	2		3	4

x1	В		В
x2				В	В

x3	В				В

x4			В	В

x5	В			В
x6			В		В
bi	100		80	40	60

Запишем задачу линейного программирования следующим образом

L = x1 + x2 + x3 + x4 + x5 + x6

при следующих ограничениях

x2 + x4 + x6 ³ 100; x2 + x3 + x5 ³ 80; x1 + x3 + x6 ³ 40; x1 + x4 +x5 ³ 60; x j ³ 0.

Введем базисные переменные и перепишем ограничения в виде, удобном для использования симплекс-метода

y1 = -100 - (-x2 - x4 - x6 ); y2 = -80 - (-x2 - x3 - x5 ); y5 = -40 - (-x1 - x3 - x6 ); y4 = -60 - (x1 - x4 - x5 );

L = 0 - (-x1 - x2 - x3 - x4 - x5 - x6 ).

109

Запишем решение в виде таблицы

			bi		x1		x2		x3		x4			x5			x6

	0			-1		-1		-1		-1		-1			-1
L	60			0		-1		-1			-1			0			-1

		-100		0		0		-1		-1		0			-1
y1	-40			1		0		-1			-1			0			-1
	-80			0		-1		-1		0		-1			0
y2	-80			0		-1		-1			0			-1			0

	-40			-1		0		-1		0		0			-1
y3	-40			-1		0		-1			0			0			-1

	-60			-1		0		0				-1			0
y4	60			1		0		0			-1			1			0
Выбираем разрешающий элемент, находим														l = -1			и
переводим базисную переменную y4 в разряд свободной x4 .
Перепишем таблицу заменяя y4 « x4 .

			bi		x1		x2		x3		y4			x5			x6

L			60		0		-1		-1	-1			0			-1
			120		1		-1		-1		0			1			0
y1			-40		1		-1		-1	-1			0	1		-1
			40		1		-1		-1		-1			1			-1
y2			-80		0		-1		-1	0	0		-1	-1		0	0
			-40		1		-1		-1		0			-1			0
y3			-40		-1		0		-1	0	0		0	0		-1
			40		1		0		-1		0			0			1
x4			60		1		0		1	-1	-1		1	1		0	0
			60		1		0		-1		-1			1			0

110

Выберем разрешающий элемент и перепишем таблицу,
заменяя	y3 « x3
	bi		x1	x2	y3	y4	x5		x6
L	100		1	-1	-1	0	1		0
	140			1
y1	-40		1	-1	0	-1	1		-1
	0			1
y2	-40	1	-1	-1	0		-1	-1	0
	40		-1	-1	1		0	-1	0
x3	40		1	0	-1	0	0		1
	40			0
x4	60		1	0	0	-1	1		0
	60			0
Выберем разрешающий элемент и перепишем таблицу,
заменяя	y2 « x2

	bi		x1		y2			y3	y4	x5	x6

L	140		2			1		0	0	2	0
y1	0		2			1		1	-1	1	-1
x2	40		-1	- 1			- 1		0	-1	0

x3	40		1			0		-1	0	1	1
x4	60		1			0		0	- 1	1	0
Целевая		функция			Lmin =140			при	x2 = 40,	x3	= 40,
x4 = 60, x1 = x5 = x6 =0.						111

4. Задача нахождения кратчайшего пути

1°. Граф задается конечным множеством вершин или узлов ( a1 , a2 ,..., an ) и множеством дуг или ребер ( l1 , l2 ,...,lm ),

соединяющих некоторые или все вершины. Если ребра ориентированы, что обычно показывают стрелками, то они называются дугами, а граф с такими ребрами называется

ориентированным графом. Если ребра графа не имеют ориентации, то граф называютнеориентированным. Каждая

дуга может быть задана упорядоченной парой вершин(ai a j ) ,

где ai - называется начальной, а a j — конечной вершиной дуги.

Сетью называется граф, каждой дуге которого поставлено в соответствие некоторое неотрицательное число. Эти числа могут выражать длину, пропускную способность, стоимость перевозки и т.п. Иногда сеть ассоциируется с транспортной сетью или сетью связи.

Путем в графе называют последовательность дуг или

вершин, в	которой каждая конечная вершина является
начальной вершиной следующего ребра. Простым путем
называется	путь, в котором каждая вершина обходится не

более одного раза. Если в простом пути ориентации дуг не совпадают, то такой путь называетсяпростой цепью. Граф, в котором каждая пара вершин соединена некоторой цепью, называется связным. Задача нахождения кратчайшего пути между двумя заданными вершинами представляет одну из главных задач теории сетей.

2°. Пусть требуется найти кратчайшие пути от одной вершины ко всем остальным вершинам сети.

Алгоритм Флойда. 1) Введем матрицу Cij , в которой записаны длины всех дуг сети

112

ì0, если i=j;

С = íдлине дуги между вершинами ai и a j ;

ïî¥, если дуги между ai и a j нет.

Положим k = 1 .

2)Для всех i ¹ k и j ¹ k осуществить операцию

Cij := {Cij , Cik + Ckj }.

3)Если k = m, вычисления закончены, иначе перейти к п. 4. 4) k := k +1 и перейти к шагу 2.

Алгоритм применим и для отрицательных длин ребер.

3°.	Алгоритм Дейкстры. Алгоритм	позволяет найти
кратчайшие пути от заданной вершины до всех остальных.
Обозначим: Сij - расстояние от узла ai до a j ;
li¢ — временная пометка для вершины ai ,		li — постоянная
пометка для вершины ai ; m — число вершин в сети.
Полагаем:
1. ls	= 0, li = ¥ для i = 1,...,m; i ¹ s; k = 1;	p = s.

2. Для всех соседей вершины a p с временными пометками

изменить пометки по формуле

li¢ = min(li¢, l p + C pi ).

3. Для всех вершин, имеющих временные пометки, найти lr = min li¢.

4. Положить p = r, k := k +1. Если k = m , вычисления закончены, иначе перейти к шагу 2.

4.1. Пусть дана сеть (рис. 1.3). Найти кратчайшие пути

между всеми узлами.	113

Рис. 1.3

Решение. Составим исходную матрицу

		1	2	3	4	5	6
1		0	1	¥	¥	¥	5
2		1	0	3	¥	6	2
	3	¥	3	0	5	1	3
	3	¥	3	0	5	1	3
	4	¥	¥	5	0	1	¥
	5	¥	6	1	1	0	3
	5	¥	6	1	1	0	3
	6	5	2	3	¥	3	0

При k =1 матрица не меняется, поэтому рассмотрим

случай, когда k = 2.
C13	= min(C13 , C12	+ C23 ) = min( ¥,1 + 3) = 4;
C14	= min(C14 , C12	+ C24 ) = min(¥,1 + ¥) = ¥;
C15	= min(C15 , C12	+ C25 ) = min(¥,1 + 6) = 7;
C16	= min(C16 , C12	+ C26 ) = min(5,1 + 2) = 3.
Найдем элементы матрицы во второй строке матрицы
C21	= min(C21 , C22	+ C21 ) = min(1,1) = 1;
C22	= 0;
C23	= min(C23 , C22	+ C23 ) = min(3,3) = 3;
C24	= min(C24 , C22	+ C24 ) = min( ¥, ¥) = ¥;
C25	= min(C25 ,C22	+ C25 ) = min(6,6) = 6;
		114

C26	= min(C26 ,C22	+ C26 ) = min( 2,2) = 2.
Для третьей строки найдем
C31	= min( C31 ,C32	+ C21 ) = min( ¥,3 +1) = 4;
C32	= min(C32 ,C32	+ C22 ) = min(3,3) = 3;
C33 = 0 ;
C34	= min(C34 ,C32	+ C24 ) = min(5,3 + ¥) = 5;
C35	= min(C35 ,C32	+ C25 ) = min(1,3 + 6) = 1;
C36	= min(C36 ,C32	+ C26 ) = min(3,3 + 2) = 3;
Для четвертой строки
C41	= min(C41 , C42	+ C21 ) = min( ¥, ¥ +1) = ¥;
C42	= min(C42 ,C42	+ C22 ) = ¥;
C43	= min(C43 ,C42	+ C23 ) = min(5, ¥ + 3) = 5;
C44	= 0;
C45	= min(C45 , C42	+ C25 ) = min(1, ¥ + 6) = 1;
C46	= min(C46 ,C42	+ C26 ) = min(¥, ¥ + 2) = ¥.
Пятая строка примет вид
C51	= min( C51 , C52	+ C21 ) = min(¥,6 +1) = 7;
C52	= min(C52 ,C52	+ C22 ) = min( 6,6) = 6;
C53	= min(C53 ,C52	+ C23 ) = min(1,6 + 3) = 1;
C54	= min(C54 ,C52	+ C24 ) = min(1,6 + ¥) = 1;
C55	= 0;
C56	= min(C56 ,C52	+ C26 ) = min(3,6 + 2) = 3.
Элементы шестой строки
C61	= min(C61 , C62	+ C21 ) = min(5,2 +1) = 3;
C62	= min(C62 , C62	+ C22 ) = min( 2,2) = 2;
C63	= min(C63 ,C62	+ C23 ) = min(3,2 + 3) = 3;
C64	= min(C64 , C62	+ C24 ) = min( ¥,2 + ¥) = ¥;
C65	= min(C65 ,C62	+ C25 ) = min(3,2 + 6) = 3;
		115

C66 = 0.

Матрица, полученная после второй итерации, имеет вид

		1	2		3	4	5		6
1		0		1	4	¥	7		3
	2	1	0		3	¥	6	2

	3	4	3		0	5	1	3
4		¥	¥		5	0	1	¥
5		7	6		1	1	0	3
6		3	2		3	¥	3	0

Рассмотрим случай, когда k = 3

C12 = min(C12 , C13 + C32 ) = min(1,4 + 3) = 1;

C13 = min(C13 , C13 + C33 ) = 4;

C14 = min(C14 , C13 + C34 ) = min( ¥,4 + 5) = 9; C15 = min(C15 , C13 + C35 ) = min( 7,4 +1) = 5; C16 = min(C16 , C13 + C36 ) = min( 3,4 + 3) = 3.

Для второй строки получим

C23 = min(C23 , C23 + C33 ) = 3;

C24 = min(C24 , C23 + C34 ) = min( ¥,3 + 5) = 8; C25 = min(C25 ,C23 + C34 ) = min( 6,3 +1) = 4.

Приведем теперь расчет элементов, которые меняют свои значения

C34	= min(C34 , C33	+ C34 ) = min(5,5) = 5;
C41	= min(C41 , C13	+ C31 ) = min( ¥,5 + 4) = 9;
C42	= min(C42 , C43	+ C32 ) = min( ¥,5 + 3) = 8;
C43	= min(C43 , C43	+ C33 ) = 5;
C46	= min(C46 , C43	+ C36 ) = min( ¥,5 + 3) = 8;
C51	= min(C51 , C53 + C31 ) = min(7,1 + 4) = 5;
C52	= min(C52 , C53	+ C32 ) = min( 6,1 + 3) = 4;
C64	= min(C64 ,C63	+ C34 ) = min(¥,3 + 5) = 8.
		116

Матрица, полученная после третьей итерации, будет

	1	2	3	4		5		6
1	0	1	4		9	5		3
2	1	0	3	8		4	2
3	4	3	0	5		1	3
4	9	8	5	0		1	8
5	5	4	1	1		0	3
6	3	2	3	4		3	0

Приведем расчет для k= 5 только тех элементов, которые

меняются
C14	= min(C14 , C15		+ C54 ) = min( 9,5 +1) = 6;
C24	= min(C24 ,C15		+ C54 ) = min(8,4 +1) = 5;
C34 = min(C34 , C35			+ C54 ) = min(5,1 +1) = 2;
C41 = min(C41 ,C45			+ C51 ) = min(9,1 + 5) = 6;
C42	= min(C42 ,C45		+ C52 ) = min(8,1 + 4) = 5;
C46	= min(C46 ,C45		+ C56 ) = min(8,1 + 3) = 4.
Таким образом, кратчайшие пути между всеми узлами
		1	2	3	4	5	6
1		0	1	4	6	5	3
2		1	0	3	5	4	2
3		4	3	0	2	1	3
4		6	5	2	0	1	4
5		5	4	1	1	0	3
6		3	2	3	4	3	0

4.2. Для сети, представленной на рис. 1.3, найти кратчайшие пути от вершины а1 до остальных.

Решение. Результаты расчетов приведены в таблице.

k	p	l1	l2	l 3	l 4	l 5		l 6
1	1	0	¥	¥	¥	¥	¥
2	2	0	1	¥	¥	¥	5
3	6	0	1	4	¥	7		3
4	3	0	1	4	¥	6	3
5	4	0	1	4	9	5	3
6	5	0	1	4	6	5	3

В первом столбце дается номер итерации, во втором — номер вершины, получающей на данной итерации постоянную пометку, а в остальных — величины пометок для каждой вершины. Столбец выделяется жирными линиями, начиная с той итерации, на которой пометка соответствующей вершины

стала постоянной. Рассмотрим порядок расчета.
1.	На	первой		итерации		пометка		первой	вершины
постоянная		и	равнаl1 = 0 ,		пометки		остальных вершин
временные и равны li = ¥.
2.	Соседями		вершины а1 является			а2	и а6 .	Временные
пометки этих вершин равны
l2¢ = min( ¥,0 +1) = 1;				l6¢ = min(¥,0 + 5) = 5.
Выбираем минимальную из них l2¢ = 1; p = 2; l p								= 1.
3.	На	третьей итерации соседями					вершиныа2 являются
вершины a3 , a5 , a6 . Временные пометки этих вершин
l2¢ = min( ¥,1 + 3) = 4;				l5¢ = min( ¥,1 + 6) = 7;
l6¢ = min(5,1 + 2) = 3.
Минимальная			из	нихl6¢	становится		постояннойl6		= 3,
p = 6.

118

117

4. Соседями	вершины а6 являются		a3 , a5 .	Временные
пометки этих вершин l3¢ = min( 4,3 + 3) = 4;			l5¢ = min(7,3 + 3) = 6.
Минимальная из них l3¢ становится постоянной l3 = 4, p = 3.
5. На пятой итерации соседями вершиныa3				являются
вершины a4 , a5 . Найдем временные пометки этих вершин
l4¢ = min( ¥,4 + 5) = 9; l5¢ = min(6,4 +1) = 5.
Минимальная из них l5¢ = 5 становится			постоянной l5 = 5,
p = 5.
6. Вершина a5	соседствует с	вершинойa4 ,		временная
пометка которой l4¢ = min(9,5 +1) = 6,		p5 = 4.

Таким образом, кратчайшие пути от первой вершины ко всем остальным приведены в вершинах выделенных столбцов и совпадают с первой строкой матрицы алгоритма Флойда предыдущей задачи.

5. Алгоритмы определения максимального потока

1°. Пусть		в	сети		имеется	единственный		источникa
								0
единственный сток an . Обозначим положительным числом bij
пропускную	способность дуги					от ai к a j ,	а	за b ji -
пропускную способность дуги от a j к ai ,причем выполнение
равенства	bij = b ji		не		обязательно. Потоком		в	сетииз
источника	a0		в		сток an	называется		множество
неотрицательных чисел xij					, поставленных в соответствие дугам
					ì-u, j = 0,
сети, таких, что					ï	j ¹ 0, n,
сети, таких, что		å xij - å x jk = í0,				j ¹ 0, n,
		i		k	ï	j = n,
					îu,	j = n,

где 0 £ xij £ bij ; число u ³ 0 называется величиной потока.

2°. Пусть начальные пропускные способности дуг заданы. Выберем некоторый начальный поток, например, нулевой.

Алгоритм работает следующим образом.

1. Выберем путь из a0 в an положительной пропускной способности q , гдеq - минимальная величина из пропускных способностей .дуг Источник a0 считается вначале

помеченным, но не просмотренным, а все остальные узлы не помеченными.

2. Выбрать любой помеченный, но не просмотренный узел

ai .
3.	Всем узлам a j		, для которых bij ³ 0 , приписать пометки
( i, j )	и	считать	их	помеченными. Считать	узел a0

просмотренным. Если при этом сток an оказался помеченным,

то по пометкам легко восстановить искомый путь из a0 в an .

В противном случае следует перейти к шагу 2. Если это невозможно, то искомого пути не существует.

4. Пусть (a0

, ai ),

(ai

, ai

), …, (ai

-1

, ai

) — найденный путь.

Тогда для каждой дуги

(ai , ai

) ^),

входящей в этот путь,

k +1

следует выполнить операторы:

xi i

k +1

:= xi i

+q; bi i

:= bi i

-q;

k k +1

bi i

:= bi

+q; u := u +q.

k +1 k

Далее переходим к шагу1. Если пути положительной пропускной способности не существует, то полученный поток является максимальным.

5.1. В области имеется семь городов, соединенных дорогами. Граф задачи показан на рис. 1.4.

120

119

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.24 Mб22764.pdf
#
15.11.20222.24 Mб22765.pdf
#
15.11.20222.25 Mб02768.pdf
#
15.11.20222.27 Mб02773.pdf
#
15.11.20222.28 Mб22777.pdf
#
15.11.20222.28 Mб02780.pdf
#
15.11.20222.29 Mб02784.pdf
#
15.11.20222.29 Mб12787.pdf
#
15.11.20222.3 Mб02788.pdf
#
15.11.20222.3 Mб32790.pdf
#
15.11.20222.31 Mб02791.pdf

		1	2	3	4	5	6
1		0	1	¥	¥	¥	5
2		1	0	3	¥	6	2
	3	¥	3	0	5	1	3
	3	¥	3	0	5	1	3
	4	¥	¥	5	0	1	¥
	5	¥	6	1	1	0	3
	5	¥	6	1	1	0	3
	6	5	2	3	¥	3	0

k	p	l1	l2	l 3	l 4	l 5		l 6
1	1	0	¥	¥	¥	¥	¥
2	2	0	1	¥	¥	¥	5
3	6	0	1	4	¥	7		3
4	3	0	1	4	¥	6	3
5	4	0	1	4	9	5	3
6	5	0	1	4	6	5	3

		1	2	3	4	5	6
1		0	1	¥	¥	¥	5
2		1	0	3	¥	6	2
	3	¥	3	0	5	1	3
	3	¥	3	0	5	1	3
	4	¥	¥	5	0	1	¥
	5	¥	6	1	1	0	3
	5	¥	6	1	1	0	3
	6	5	2	3	¥	3	0

k	p	l1	l2	l 3	l 4	l 5		l 6
1	1	0	¥	¥	¥	¥	¥
2	2	0	1	¥	¥	¥	5
3	6	0	1	4	¥	7		3
4	3	0	1	4	¥	6	3
5	4	0	1	4	9	5	3
6	5	0	1	4	6	5	3

		1	2	3	4	5	6
1		0	1	¥	¥	¥	5
2		1	0	3	¥	6	2
	3	¥	3	0	5	1	3
	3	¥	3	0	5	1	3
	4	¥	¥	5	0	1	¥
	5	¥	6	1	1	0	3
	5	¥	6	1	1	0	3
	6	5	2	3	¥	3	0

k	p	l1	l2	l 3	l 4	l 5		l 6
1	1	0	¥	¥	¥	¥	¥
2	2	0	1	¥	¥	¥	5
3	6	0	1	4	¥	7		3
4	3	0	1	4	¥	6	3
5	4	0	1	4	9	5	3
6	5	0	1	4	6	5	3