
2780
.pdfт.е. крайние линии уровня целевой функции, имеющие общие точки с ОДР.
4) Определить координаты экстремальных точек (Р = р ∩ ОДР, Q = q ∩ ОДР) и вычислить значения целевой функции в них.
Примечания.
1)Если ОДР — пустое множество, то задача не имеет решения в виду несовместности системы ограничений.
2)Если ОДР неограничена по направлению вектора n =
(с1,с2), то сама |
целевая функция неограничена |
сверху в |
этой области, |
и принимаем Lma x (Х) = + ∞. |
Если ОДР |
неограничена в направлении, противоположном n, то
принимаем Lmi n (Х) = - ∞.
3.3. Графически может быть решена также задача линейного программирования, заданная в канонической форме, при условии n - r > 2 (n — число переменных, r — ранг системы уравнений). Для этого задачу надо привести к симметрическому виду. Графический метод можно распространить и на более общие ситуации, например, в случае, когда условия неотрицательности распространяются не на все переменные.
Решим графически задачи линейного программирования (примеры 3.1 - 3.7).
Пример 3.1.
L(X ) = 4x1 +7x2 +6 → extr,
1)2x1 −3x2 ≤ 6,
2)x1 + x2 ≤10,
3)2x1 +2x2 ≥ 3,
4)2x1 − x2 ≥ 0,
5)x ≤ 6,1
x1 ≥ 0, x2 ≥ 0.
21
Решение.
а) Область допустимых решений, которую обозначим буквой G, построим следующим образом. Построим прямые с
уравнениями |
|
|
|
x1 |
|
0 |
|
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
1) |
2x1 |
- 3x2 |
=6, |
|
|
|
|
|
|
|
|
|||||||
|
x2 |
|
-2 |
|
0 |
|
|
|
|
|
||||||||
2) x1 + x2 =10, |
|
x1 |
|
0 |
|
|
|
10 |
|
|
|
|
||||||
|
|
|
|
|||||||||||||||
|
x2 |
|
10 |
|
|
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3) |
2x1 |
+ 2x2 |
=3, |
|
x1 |
|
0 |
|
|
|
3/2 |
|
|
|||||
|
|
|
|
|||||||||||||||
|
x2 |
|
3/2 |
|
|
|
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) |
2x1 |
- x2 =0, |
|
x1 |
|
0 |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
x2 |
|
0 |
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5) |
- 7) |
x1 = 6, x1 = 0, |
|
|
x2 = 0, |
|||||||||||||
Прямые |
пронумерованы, а |
|
рядом с соответствующим |
|||||||||||||||
уравнением приведены координаты двух точек, через которые проходит прямая. Номер прямой имеется также на чертеже
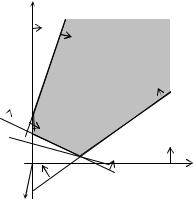
(рис. 3.1).
б) Каждое неравенство, фигурирующее в системе ограничений, определяет полуплоскость, причем эта полуплоскость содержит точку, координаты которой удовлетворяют соответствующему строгому неравенству.
Легко видеть, что первые два и четвертое неравенства системы ограничений удовлетворяются координатами точки O(0,0). Поэтому три полуплоскости содержат начало координат системы Ox1x2.
На соответствующую полуплоскость указывают стрелки, идущие от каждой прямой. Жирной линией выделим границу ОДР — выпуклый шестиугольник АВСDЕF. Заметим, что последние неравенства х1 > 0, x2 > 0, означающие неотрицательность переменных задачи, определяют первую четверть плоскости Ох1 х2 .
22
|
x2 |
|
|
|
1) |
|
|
|
|
|
G |
4 |
C |
|
2) |
3) |
B |
|
|
q |
|
|
|
3 |
|
A |
|
0 |
|
|
|
|
|
|
|
n |
2 |
4 |
x1 |
|
|
||
|
|
|
|
|
Рис. 3.1 |
|
|
б) Каждое неравенство, |
фигурирующее в системе |
||
ограничений, определяет полуплоскость, причем эта полуплоскость содержит точку, координаты которой удовлетворяют соответствующему строгому неравенству.
Легко видеть, что первые два и четвертое неравенства системы ограничений удовлетворяются координатами точки O(0,0). Поэтому три полуплоскости содержат начало координат системы Ox1 x2 .
На соответствующую полуплоскость указывают стрелки, идущие от каждой прямой. Жирной линией выделим границу ОДР — выпуклый шестиугольник АВСDЕF. Заметим, что последние неравенства х1 > 0, x2 > 0, означающие неотрицательность переменных задачи, определяют первую
четверть плоскости Ох1 х2 . |
вектор |
целевой |
||
в) Строим теперь нормальный |
||||
функции n |
= |
(4,7). Подчеркнем, что |
его направление |
|
указывает |
на |
направление возрастания |
целевой функции |
|
L(Х) = 4x1 + 7х2. |
|
|
||
|
|
23 |
|
|
Прямая с уравнением 4x1 + 7x2 = 0 представляет собой «нулевую» линию уровня функции z = 4х1 + 7х2. Эта прямая проходит через начало координат и перпендикулярна нормальному вектору n = (4,7). Передвигаем эту прямую параллельно себе, или перпендикулярно n, и фиксируем два ее крайних положения.
Эти крайние прямые, которые обозначим буквами р и q, должны иметь с границей G либо общую вершину, либо общий отрезок, причем направление от р к q совпадает с направлением n. В нашем случае р проходит через точку А, а q
— через точку Е. Эти прямые называются соответственно нижней и верхней опорными прямыми для G.
г) Определим координаты точек А и Е. На чертеже видим, что точка А лежит на прямых 3) и 7), а Е — на 2) и 4). Именно поэтому мы пронумеровали уравнения прямых и их изображения. Теперь легко составить системы уравнений для определения координат этих точек.
Запишем это так:
A : 2x1 +3x2 = 3, A(3/ 2,0);
x2 = 0,
E : x1 + x2 =10, E(10 / 3, 20 / 3)
2x1 − x2 = 0,
Вычислим значения целевой функции в точках А и Е:
L(3/2,0) = 12,
L(10/3,20/3) = 66,
Этим задача решена.
Ответ: Lmin = L(3/2,0) = 12, Lmax = L(10/3,20/3) = 66.
24
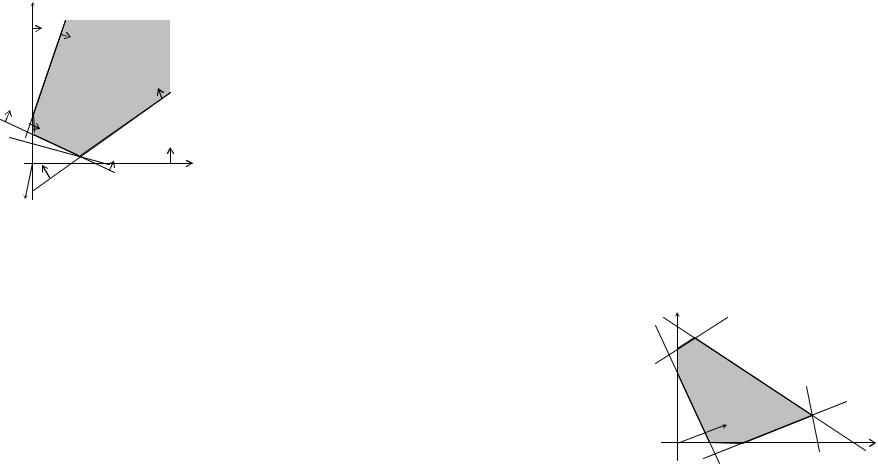
Пример 3.2.
|
x2 |
|
|
|
1) |
|
|
|
|
|
G |
4 |
C |
|
2) |
3) |
B |
|
|
q |
|
|
|
3 |
|
A |
|
0 |
|
|
|
|
|
|
|
n |
2 |
4 |
x1 |
|
|
||
|
|
|
Рис.3.2
L(
1)
2)
3)
X ) =15 − x1 −2x2 → extr,
|
|
|
|
|
|
|
|
−2x + x |
|
≤ 4, |
|||
|
|
1 |
|
2 |
|
|
|
x1 |
−2x2 |
|
≤ 2, |
||
|
|
|||||
3x |
+4x |
|
≥12, |
|||
|
1 |
|
|
2 |
|
|
x + x |
2 |
≥ −5, |
||||
|
1 |
|
|
|
|
|
x1 ≥ 0, x2 |
≥ 0. |
|||||
Решение. Четвертое неравенство системы не учитываем, так как оно тривиальное.
Область допустимых решений G представляет собой область, неограниченную в направлении, противоположном вектору целевой функции n = (-1,-2) (рис. 3.2). Верхняя опорная прямая проходит через точку А.
Нижняя опорная прямая р не существует, так как каждая прямая с уравнением –х1 - 2x2 = С при С < - 6 имеет общие точки с G. Другими словами, для области G нет прямой, которая бы ее ограничивала в направлении, противоположном n.
Имеем
A : 3x1 +4x2 =12, A(16 / 5,3/ 5),
x1 −2x2 = 2,
L(16 / 5,3 / 5) = 53 / 5.
Ответ: Lmi n = -∞; Lma x = L(16/5, 3/5) = 53/5.
25
Пример 3.3.
L(X ) = 2x1 + x2 → extr,
1)−x1 + x2 ≤ 6,
2)2x1 + x2 ≥ 4,
3)x1 −2x2 ≤ 4,
4)x1 + x2 ≤10,
x1 ≥ 0, x2 ≥ 0.
Решение. Область G представляет собой шестиугольник AВСDЕF (рис. 3.3). Вектор n = (2,1) показывает, что целевая функция L(Х) = 2х1 + х2 принимает максимальное значение в точке С(8,2), а минимальное — во всех точках отрезка АF (нижняя опорная прямая р совпадает с прямой АF, ее уравнение 2х1 + х2 = 4). Таким образом,
|
x2 |
1) |
|
|
|
|
|
|
|
2) |
10 E6 D |
|
4) |
|
|
4 F |
|
|
|
|
|
q |
|
|
|
|
|
3) |
|
|
|
|
|
|
|
|
n |
C |
|
|
|
|
|
|
|
0 |
А B |
|
x1 |
|
2 |
4 |
|
10 |
|
|
p |
|
|
Рис.3.3
Lmax = L(8,2) = 18,
Lmin = L(2,0) = (0,4) = 4.
Задача на минимум имеет бесконечное множество решений, каждое из них представляет собой выпуклую
26
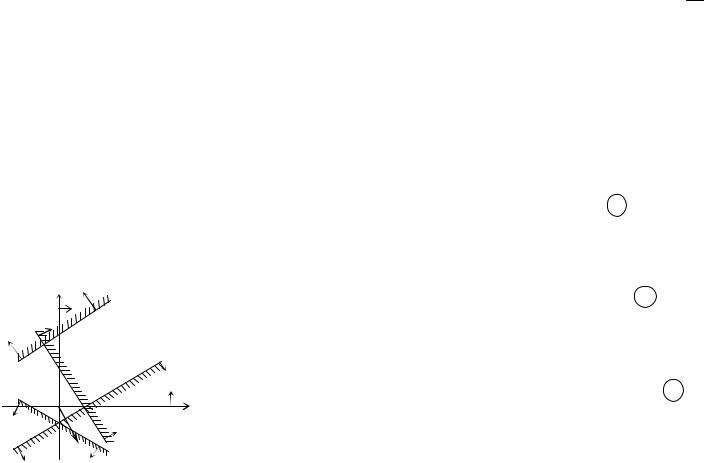
линейную комбинацию решений Х1 = (2,0) и Х2 = (0,4); записываем это в виде
X = tX1 + (1-t)X2 , t [0,1]
Ответ: Хm a x = (8,2), X1 , mi n = (2,0), X2 , mi n = (0,4), Xmi n = t(2,0)+(1 - t)(0,4), Lma x = 18,Lmi n = 4.
Пример 3.4.
L(X ) =1+2x1 −3x2 → extr,
1)−2x1 + x2 ≥ 4,
2)x1 + x2 ≥ 2,
3)x1 +2x2 ≤ −1,
4)x1 − x2 ≤ 2,
x1 ≥ 0, x2 ≥ 0.
Решение. Заметим, что полуплоскости, определяемые системой неравенств данной задачи, не имеют общих точек. ОДР — пустое множество (рис. 3.4).
x2 |
1) |
|
2) |
||
|
|
|
4) |
Ответ: |
задача |
не |
3) |
|
имеет решения |
по |
||
|
|
||||
|
0 |
|
причине |
несов- |
|
|
|
местности |
условий |
||
|
|
|
|||
x1 |
задачи. |
|
|
n |
|
Рис.3.4 |
27 |
|
Пример 3.5. Графическим методом решить задачу:
L(X ) = 3x1 +2x2 − x3 +5x5 → extr,
x1 +2x2 −3x3 +11x4 +8x5 = −8,−2x1 + x2 + x3 −7x4 +9x5 = 6,x1 + x2 + x3 +2x4 −6x5 = 27,
xj ≥ 0, j =1,5.
Решение. Система ограничений состоит из трех уравнений с пятью неизвестными (n = 5, m = 3, n - m = 2). Систему уравнений решим относительно каких-либо трех неизвестных. Сделаем это при помощи таблицы Гаусса (табл. 3.1), которая приведена ниже. Одновременно мы выразим и целевую функцию через свободные неизвестные решенной системы.
Таблица 3.1
x1 |
x2 |
x3 |
x4 |
|
x5 |
св.чл. |
1 |
2 |
-3 |
11 |
|
8 |
-8 |
-2 |
1 |
1 |
-7 |
9 |
6 |
|
1 |
1 |
1 |
2 |
-6 |
27 |
|
3 |
2 |
-1 |
0 |
5 |
L |
|
1 |
2 |
-3 |
11 |
8 |
-8 |
|
0 |
5 |
-5 |
15 |
25 |
-10 |
|
0 |
-1 |
4 |
-9 |
-14 |
35 |
|
0 |
-4 |
8 |
-33 |
-19 |
L+24 |
|
1 |
0 |
-1 |
5 |
-2 |
4 |
|
0 |
1 |
-1 |
3 |
5 |
-2 |
|
0 |
0 |
3 |
-6 |
-9 |
33 |
|
0 |
0 |
4 |
-21 |
1 |
L+16 |
|
1 |
0 |
0 |
3 |
-5 |
7 |
|
0 |
1 |
0 |
1 |
2 |
9 |
|
0 |
0 |
1 |
-2 |
-3 |
11 |
|
0 |
0 |
0 |
-13 |
13 |
L-28 |
|
|
|
|
|
28 |
|
|
Из последнего блока табл. 3.1 получаем систему, разрешенную относительно базисных переменных х1, х2 и х3:
x |
= 7 −3x |
+5x , |
|
|
1 |
4 |
|
5 |
|
x2 |
= 9 − x4 − |
2x5 , |
(*) |
|
x |
=11+2x |
|
+3x |
|
4 |
, |
|||
3 |
|
5 |
||
и целевую функцию, выраженные через свободные переменные
L(X) = - 13x4 + 13x5 +28.
Систему (*) заменим системой неравенств (х1>0, х2 >0, х3 >0):
7 −3x |
|
+5x ≥ 0, |
3x |
|
−5x |
|
≤ 7, |
|
|
4 |
5 |
|
4 |
5 |
|
|
|
9 − x4 |
−2x5 ≥ 0, x4 |
+2x5 |
≤ 9, |
(**) |
||||
|
|
|
|
|
+3x5 ≥ −11. |
|||
11+2x4 +3x5 ≥ 0, |
2x4 |
|
||||||
Первоначальная задача может быть переформулирована так: при заданных ограничениях в виде системы неравенств с двумя переменными найти экстремум линейной целевой функции L(Х) = - 13х4 + 13х5 + 28.
Очевидно, что третье неравенство системы можно отбросить как тривиальное: если х4>0 и x5>0, то 2x4 +3х5 > -11.
Построив ОДР (это четырехугольник в плоскости Ox4x5, постройте его самостоятельно), обнаруживаем, что целевая функция достигает максимального значения в точке А(0; 4,5) и минимального в точке
B : 3x4 −5x5 = 7,
x4 +2x5 = 9,
т.е. в точке B(59/11,20/11). При этом L(А) = 86,5, L(В) = - 199/11. Вспомним, что наша задача имеет пять неизвестных. Находим значения остальных неизвестных из уравнений, выражающих значения x1, x2, x3 через x4 и x5. Получаем:
если х4 = 0, х5 = 4,5, то x1 = 7 - 3 • 0 + 5 • 4,5 = 29,5, х2 = 0, х3 = 28,5;
если x4 = 59/11, х5 = 20/11, то х1 =0, х2 = 0, х3 = 299/11.
Задача решена полностью.
Ответ: Lmin = L(0;0;299/11;59/11;20/11) = -199/11, Lmax = L(29,5; 0; 24,5; 0; 4,5) = 86,5.
Пример 3.6. Графическим методом решить задачу:
L(X ) = 2x1 + x2 −3x3 +2x4 → max,
2x1 − x2 +3x3 + x4 = 4,x1 +2x2 +3x3 +2x4 = 6,3x1 − x2 −2x3 + x4 ≥ 2,5x1 +3x2 + x3 ≤ 6,
|
+ x2 |
−3x3 −2x4 |
≤ 4, |
−2x1 |
x1 ≥ 0, x2 ≥ 0,
Решение. Заметим, что в задаче отсутствуют условия неотрицательности для переменных х3 и х4. Этим она отличается от задачи 3.5.
1) Приводим сначала задачу к неполному каноническому виду. Для этого используем предложения U.1 и U.2 из п. 1.4 (с их помощью переходим от неравенств к равенствам). Новая задача, условно говоря, полуканоническая, потому что условия неотрицательности переменных х3 и х4 остаются невыполненными. Задача имеет следующий вид (коэффициенты при дополнительных переменных x5, х6 и х7 в целевой функции принимаются равными нулю):
29 |
30 |
|

F (X ) = 2x1 + x2 −3x3 +2x4 +0x5 +0x6 +0x7 → max,
2x1 − x2 +3x3 + x4 = 4,x1 +2x2 +3x3 +2x4 = 6,3x1 − x2 −2x3 + x4 − x5 = 2,5x1 +3x2 + x3 + x6 = 6,
|
+ x2 |
−3x3 −2x4 + x7 |
= 4, |
−2x1 |
x1 ≥ 0, x2 ≥ 0, x5 ≥ 0, x6 ≥ 0, x7 ≥ 0.
2) Дальнейшая схема решения такова. Те переменные, на которые условия неотрицательности не распространяются (это х3 и х4), будем исключать из системы условий. Воспользуемся таблицей Гаусса (табл. 3.2).
Последняя строка третьего блока таблицы соответствует целевой функции, написанной в виде уравнения со свободным членом F + 46. Разрешим систему относительно х3 и х4. Из последнего блока табл. 3.2 получаем:
x |
= 6 −5x |
−3x |
|
− x , |
|
3 |
1 |
|
2 |
6 |
(*) |
x4 |
= −14 +13x1 +10x2 +3x6 . |
|
|||
Переменные х3 и х4 в остальные уравнения и в целевую функцию не входят. Временно опуская полученные уравнения системы (*) сформулируем новую задачу:
F (X ) = 43x1 +30x2 +9x6 −46 → max,
12x1 +13x2 +3x6 =16,26x1 +15x2 − x5 +5x6 = 28,13x1 +10x2 +3x6 − x7 = 6,
x1 ≥ 0, x2 ≥ 0, x5 ≥ 0, x6 ≥ 0, x7 ≥ 0.
31
Таблица 3.2
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
св.чл |
2 |
-1 |
3 |
1 |
0 |
0 |
0 |
4 |
1 |
2 |
3 |
2 |
0 |
0 |
0 |
6 |
3 |
-1 -2 1 -1 0 0 |
2 |
|||||
5 |
3 |
1 |
0 |
0 |
1 |
0 |
6 |
-2 |
1 |
-3 -2 0 |
0 1 |
4 |
|||
2 |
1 |
-3 |
2 |
0 |
0 |
0 |
F |
-13 -10 0 |
1 |
0 |
-3 0 |
-14 |
|||
-14 -7 |
0 |
3 |
0 |
-3 |
0 |
-12 |
|
13 |
5 |
0 |
1 |
-1 |
2 |
0 |
14 |
5 |
3 |
2 |
0 |
0 |
1 |
0 |
6 |
13 |
10 |
0 |
-2 |
0 |
3 |
1 |
22 |
17 |
10 |
0 |
2 |
0 |
3 |
0 |
F+18 |
-13 -10 0 1 0 -3 0 |
-14 |
||||||
12 |
13 |
0 |
0 |
0 |
3 |
0 |
16 |
26 |
15 |
0 |
0 |
-1 |
5 |
0 |
28 |
5 |
3 |
1 |
0 |
0 |
1 |
0 |
6 |
-13 -10 0 0 0 -3 1 |
-6 |
||||||
43 |
30 |
0 |
0 |
0 |
9 |
0 |
F+46 |
Эта задача записана в канонической форме. Число неизвестных n = 5, число уравнений m = 3 и n - m = 2 (r = m = 3), поэтому задачу можно решить геометрически.
3) Далее воспользуемся схемой решения задачи 3.5. Разрешая последнюю систему относительно х5, х6, х7,
|
x |
|
= − |
4 |
+ 6 x − |
20 |
x |
|
, |
|
||||||
|
5 |
|
|
2 |
|
|||||||||||
|
|
|
3 |
|
|
1 |
|
3 |
|
|
|
|
||||
|
|
|
|
|
12 |
|
|
|
|
|
|
|
||||
|
|
|
= |
16 |
− |
x1 − |
13 |
x |
2 , |
|
||||||
|
x6 |
3 |
3 |
3 |
|
|
||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
(**) |
||||
|
= 18 |
+ 37 x + 37 x |
|
|
, |
|||||||||||
|
x |
7 |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
F(X) = 7x1 − 9 x2 |
+ 2 → max . |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
Условия х5 > 0, х6 > 0, х7 > 0 приводят к неравенствам
6x − |
20 |
x |
|
≥ |
4 |
|
, |
|
|||||||||||||
|
|
2 |
|
|
|
||||||||||||||||
|
1 |
|
3 |
|
|
|
|
|
3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
13 |
|
|
|
|
|
16 |
|
|||||||||
12 |
x1 + |
|
x2 |
≤ |
, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
3 |
||||||||||
3 |
−3x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
≥ −10, |
|
|
|
|
|
|||||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9x |
−10x |
|
≥ 2, |
|
|
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
≤16, |
|
||||||
12x1 +13x2 |
|
||||||||||||||||||||
x |
|
|
−3x |
2 |
≥ −10, |
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В последней и предпоследней системах имеется в виду, |
|||||||||||||||||||||
что х1 > 0 и х2 > 0. |
|
|
|
|
|
|
|
можно |
|
|
|
решить графически |
|||||||||
Теперь видно, что задачу |
|
|
|
|
|
||||||||||||||||
(предлагаем сделать это самостоятельно) и Fmax(Х) = F(4/3; 0) = 34/3. Зная экстремальные значения x1 = 4/3 и х2 = 0, находим значения остальных неизвестных из систем (**) и (*). Опуская значения дополнительных неизвестных х5, х6, х7, получаем х3 = -2/3 (условие х3 > 0 отсутствует), х4 = 10/3.
Ответ: Lmax(Х) = L(4/3; 0; -2/3; 10/3) = 34/3.
Вопросы для самопроверки
3.1.Какое максимальное число неравенств может содержать задача ЛП с двумя переменными?
3.2.Как строится ОДР задача ЛП с двумя переменными?
3.3.Может ли ОДР быть невыпуклым многоугольником?
3.4.Может ли ОДР быть открытым множеством? пустым?
3.5.Какая прямая называется опорной к ОДР?
3.6.Чем отличается верхняя опорная прямая от нижней?
33
3.7.Может ли линия уровня целевой функции быть параллельной вектору целевой функции?
3.8.Может ли задача ЛП с двумя переменными иметь два
итолько два оптимальных решения?
3.9.В каком случае задача ЛП с двумя переменными не имеет решения?
3.10.Каков геометрический смысл коэффициентов при неравенствах в системе ограничений? Каков смысл коэффициентов целевой функции?
3.11.Какой вывод можно делать из того, что ОДР не ограничена по направлению, противоположному вектору целевой функции?
3.12.Можно ли решить графически симметрическую задачу с тремя переменными?
3.13.Сколько переменных может содержать задача линейного программирования, которую можно решить графически?
3.14.Можно ли решить графически задачу линейного программирования, если на некоторые ее переменные не наложены условия неотрицательности?
3.15.Определить соотношения между числом переменных
ичислом ограничений, чтобы задачу можно было решить графически.
4.Симплексный метод решения задач линейного программирования
4.1.Симплексный метод применяется при решении задач линейного программирования, заданных в канонической форме (см. п. 1.2).
Симплексный метод основан на том факте, что целевая функция достигает экстремума на допустимом базисном решении. Таким образом, дело сводится к перебору базисных
34

допустимых решений системы ограничений-равенств задачи. Симплексный метод позволяет переходить от одного допустимого базисного решения к другому так, чтобы значение целевой функции уменьшалось (увеличивалось) в задаче на минимум (максимум). Все необходимые базисные решения целесообразно получить в таблице Гаусса. В первый блок таблицы заносятся данные исходной задачи. При необходимости некоторые уравнения системы ограничений следует умножать на —1 (чтобы все свободные члены
уравнений были неотрицательными).
Последнюю строку, которую назовем индексной, заполняем коэффициентами целевой функции, представленной в виде уравнения
c1 x1 + c2 x2 + … + cn xn = L(X) – c0 .
где с0 — свободный член L(Х). Вместо L — с0 записываем в первом блоке только – с0 и характер задачи (max или min), а в последующих блоках — результаты вычислений.
Первый блок таблицы Гаусса представлен в табл. 4.1.
Таблица 4.1
x1 |
x2 |
… xn |
св. чл. |
|
a11 |
a12 |
… |
a1n |
b1 |
… |
… |
… … |
… |
|
am1 |
am2 |
… |
amn |
bm |
c1 |
c2 |
… |
cn |
-c0 |
min(max)
Каждая итерация, т. е. переход от одного блока таблицы к другому осуществляется известными элементарными преобразованиями Жордана-Гаусса для строк. Они сводятся к
35
следующим действиям:
1)Сначала выбирается разрешающий (ведущий) коэффициент ap q ≠ 0. Разрешающий коэффициент нельзя брать в индексной строке.
2)Разрешающая строка делится на apq , а разрешающий столбец заменяют единичным с 1 вместо ap q .
3)Все остальные элементы (коэффициенты) блока пересчитываются по формулам
′ |
|
|
|
ap j ai q |
′ |
|
bpai q |
|
|
|
|
|
|
|
ai j =ai j |
− |
|
|
, bi |
=bi − |
|
, |
ap j |
|
|
|
|
||
apq |
apq |
|
|
|
apq |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
c′j |
=cj |
− |
ap j cq |
, i ≠ p, j ≠q, |
|
|
|
|
a'i j |
|||||
|
|
|
|
|||||||||||
|
|
|
apq |
|
|
|
|
ai j |
|
|
|
ai q |
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
напоминающим известное мнемоническое правило прямоугольника (см. схему), или арифметическими действиями над строками блока таблицы при помощи разрешающей строки, если это возможно.
При этом надо следить за тем, чтобы новые свободные члены уравнений оставались неотрицательными (об этом см.
п. 4.3 ниже).
4.2. Часть итераций предназначена для получения первого (начального) базисного решения. Предположим, что оно получено и имеет вид
X1 = (β1, β2,…, βm, 0, 0,…, 0);
тогда соответствующий блок таблицы имеет вид таблицы 4.2.
36
|
|
|
|
|
|
|
|
Таблица 4.2 |
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
… |
xm-1 |
xm |
xm+1 |
... |
xn |
св.чл. |
|
1 |
0 |
… |
0 |
0 |
α1,m+1 |
… |
α1n |
β1 |
|
0 |
1 |
… |
0 |
0 |
α2m+1 |
… |
α2n |
β2 |
|
… |
… |
… |
… |
… |
… |
… |
… ... |
||
0 |
0 |
… |
1 |
0 |
αm-1,m+1 |
… |
αm-1,n |
βm-1 |
|
0 |
0 |
… |
0 |
1 |
αm,m+1 |
… |
αm,n |
βm |
|
0 |
0 |
… |
0 |
0 |
γm+1 |
… |
γn |
0 |
|
При этом β1 > 0, β2 > 0, ..., βm > 0.
Если все компоненты базисного решения положительны (мы предполагаем, что ранг системы уравнений-условий задачи равен m, r = m), то решение называется невырожденным, в противном случае — вырожденным.
Теорема 4.1 (теорема оптимальности решения). Допустимое базисное решение Х1 = (β1, β2,..., βm,0,0,…, 0) является оптимальным в том и только в том случае, когда среди коэффициентов индексной строки нет положительных в задаче на максимум (нет отрицательных в задаче на минимум).
Если коэффициенты индексной строки имеют разные знаки, то соответствующее допустимое базисное решение не является оптимальным как в задаче на максимум, так и в задаче на минимум, и, следовательно, следует переходить к другому базисному допустимому решению (плану).
4.3. Очередное допустимое базисное решение (план) получается тем же способом, но с учетом некоторых особенностей. Ограничимся случаем задачи на максимум, поскольку задача на минимум решается по аналогичной схеме.
1) Разрешающий столбец надо выбирать так, чтобы не приобретать лишних положительных коэффициентов в индексной строке (хотя это иногда неизбежно, см. теорему оптимальности).
Иногда в качестве разрешающего берут столбец
37
максимального коэффициента индексной строки.
2)Неправильный выбор разрешающей строки может привести к недопустимому решению. Правильный ее выбор состоит в следующем.
Предположим, что выбран разрешающий столбец.
Составим отношения θi q свободных членов bi уравнений (строка целевой функции здесь не участвует) к
положительным коэффициентам ai q разрешающего столбца. Найдем минимальное из этих отношений, которое обозначим θ (в соответствующей таблице оно подчеркивается). Строку с этим числом надо считать разрешающей. Если таких строк несколько, то выбор среди них безразличен.
3)Если ведущий (разрешающий) коэффициент выбран правильно, то соответствующие элементарные преобразования приводят только к допустимому решению.
При необходимости процедура нахождения базисного допустимого решения повторяется до получения оптимального решения, если оно существует.
Заметим, что принцип выбора разрешающей строки следует соблюдать и при поиске первого базисного допустимого решения.
4.4. Рассмотрим несколько ситуаций, в которых получение оптимального решения недостижимо.
1)Предположим, что полученное базисное решение задачи на максимум не оптимально: в индексной строке имеется, например, один положительный коэффициент. Тем самым определена переменная, которую следует ввести в базис. Вместе с тем коэффициенты разрешающего столбца неположительные. Следовательно, ввести эту переменную в базис нельзя: это приводит к недопустимому решению. В таком случае задача не имеет решения по причине неограниченности целевой функции в ОДР.
2)Предположим, что при поиске первого базисного решения наталкиваемся на недопустимые решения и не
38

удается получить допустимого решения. В таком случае задача не имеет решения по причине несовместности условийограничений задачи.
Симплексным методом решим следующие примеры задач линейного программирования.
Пример 4.1.
L(X ) = x1 + x2 − x3 −3x4 −7x5 → max,
−x1 + x2 + x3 +2x4 −3x5 = 4,−x2 − x3 +4x5 = 4,
x1 + x2 +4x3 + x4 −8x5 = 3,
xj ≥ 0, j =1,5.
Решение. Задача задана в канонической форме. Заполняем первый блок таблицы Гаусса (табл. 4.3) и приступаем к поиску первого (начального) базисного допустимого решения.
Таблица 4.3
x1 |
x2 |
x3 |
x4 |
x5 |
св.чл. |
θ |
-1 |
1 |
1 |
2 |
-3 |
4 |
4:1 |
0 |
-1 |
-1 |
0 |
4 |
4 |
|
1 |
1 |
4 |
1 |
-8 |
3 |
3:1 |
1 |
1 |
-1 |
-3 |
-7 |
max |
7:2 |
0 |
2 |
5 |
3 |
-11 |
7 |
|
0 |
-1 |
-1 |
0 |
4 |
4 |
4:4 |
1 |
1 |
4 |
1 |
-8 |
3 |
|
0 |
0 |
-5 |
-4 |
1 |
-3 |
18:3 |
0 |
-3/4 |
9/4 |
3 |
0 |
18 |
|
0 |
-1/4 |
-1/4 |
0 |
1 |
1 |
|
1 |
-1 |
2 |
1 |
0 |
11 |
11:1 |
0 |
1/4 |
-19/4 |
-4 |
0 |
-4 |
|
0 |
-1/4 |
3/4 |
1 |
0 |
6 |
|
0 |
-1/4 |
-1/4 |
0 |
1 |
1 |
|
1 |
-3/4 |
5/4 |
0 |
0 |
5 |
|
0 |
-3/4 |
-7/4 |
0 |
0 |
20 |
|
Пояснения:
а) первый разрешающий коэффициент (в таблице он обведен кружком) брали в первом столбце, этот столбец наиболее простой, в нем имеем один нуль;
б) во втором блоке в качестве разрешающего брали столбец с положительным коэффициентом индексной строки; в) в базис можно ввести либо х4, либо x5, хотя ввести нужно х2, поскольку только при х2 коэффициент индексной строки положителен. С другой стороны ввести х2 нельзя, потому что все коэффициенты этого столбца отрицательные — это приведет к недопустимому решению. Поэтому в базис
ввели х4; г) получено первое базисное допустимое решение. Оно
оптимально, так как в индексной строке нет положительных коэффициентов.
Замечание: в дополнительном столбце в отношениях свободных членов уравнений к коэффициентам ведущего столбца отрицательные его коэффициенты (и нули) не участвуют.
Оптимальное решение Х1 = (5,0,0,6,1) получено одновременно с первым базисным решением. При этом Lmax = -20.
Ответ: X = (5,0,0,6,1), Lmax = -20.
Пример 4.2.
L(X ) = −7x1 −8x2 −11x3 + x4 + x5 − x6 → min,
6x1 +11x2 +8x3 − x4 − x5 = 36,
4x1 +2x2 +7x3 − x5 + x6 = 21,8x1 +8x2 +12x3 − x4 − x5 + x6 = 42,
xj ≥ 0, j =1,6.
40
39
