
2780
.pdf
F(Y ) = 6 y1 +4 y2 → min,
y1 − y2 ≥ 2,−3y1 + y2 ≥ 3,
y j ≥ 0, j =1, 2.
Очевидно, что эту задачу также можно решить графически. Исходя из построенного чертежа (рис. 5.2), заключаем, что она не имеет решения по причине несовместности системы ограничений в области неотрицательных значений переменных.
Пример 5.4. Для задачи линейного программирования составить двойственную задачу и решить обе эти задачи. Сопоставить экстремальные значения соответствующих целевых функций, а также значения основных и дополнительных переменных в основной и двойственной задачах.
L(X ) = 4x1 +3x2 +2x3 → max,
5x1 +8x2 +4x3 ≤ 400,5x1 +5x2 +6x3 ≤ 300,10x1 +2x2 +5x3 ≤ 200,
xj ≥ 0, j =1,3.
1) Сначала приведем исходную (основную) задачу к каноническому виду и решим ее симплексным методом. Очевидно, что для получения канонического вида необходимо прибавить три дополнительные неотрицательные переменные х4 , х5 , х6 соответственно к первому, второму и третьему неравенствам системы ограничений. Поэтому можно сразу обратиться к таблице Гаусса (табл. 5.1) и заполнить соответствующие блоки.
61
|
|
|
|
|
|
Таблица 5.1 |
||
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
св.чл. |
||
5 |
8 |
4 |
1 |
0 |
0 |
400 |
|
|
5 |
5 |
6 |
0 |
1 |
0 |
300 |
|
|
10 |
2 |
5 |
0 |
0 |
1 |
200 |
|
|
4 |
3 |
2 |
0 |
0 |
0 |
max |
|
|
0 |
7 |
3/2 |
1 |
0 |
-1/2 |
300 |
|
|
0 |
4 |
7/2 |
0 |
1 |
-1/2 |
200 |
|
|
1 |
1/5 |
1/2 |
0 |
0 |
1/10 |
20 |
|
|
0 |
11/5 |
0 |
0 |
0 |
-2/5 |
-80 |
|
|
0 |
1 |
3/14 |
1/7 |
0 |
-1/14 |
300/7 |
|
|
0 |
0 |
37/14 |
-4/7 |
1 |
-3/14 |
200/7 |
|
|
1 |
0 |
65/35 |
-1/35 |
0 |
4/35 |
80/7 |
|
|
0 |
0 |
-33/7 |
-11/35 |
0 |
-17/70 |
-1220/7 |
|
|
Таким образом, Хопт = (80/7,300/7,0), Lmax = 1220/7.
Значения основных переменных равны: х1 = 80/7, х2 = 300/7, х3 = 0, значения дополнительных переменных: x4 = 0, х5 = 200/7, х6 = 0.
2) Составим двойственную задачу. Это задача на минимум:
F (Y ) = 400 y1 +300y2 +200 y3 → min,
5y1 +5y2 +10 y3 ≥ 4,
8y1 +5y2 +2y3 ≥ 3,4 y1 +6y2 +5y3 ≥ 2,
y j ≥ 0, j =1,3.
Сначала изменяем направления неравенств системы условий задачи, умножая каждое неравенство на —1. Затем приводим задачу к каноническому виду:
62

|
−5 y |
−5 y |
2 |
−10 y |
3 |
≤ −4, |
|
−5 y |
−5 y |
2 |
−10 y |
3 |
+ y |
4 |
= −4, |
||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
−8 y1 −5 y2 |
− 2 y3 |
≤ −3, |
−8 y1 −5 y2 |
− 2 y3 |
+ y5 |
= −3, |
||||||||||||
|
−4 y |
− 6 y |
2 |
−5 y |
3 |
≤ −2. |
|
−4 y |
−6 y |
2 |
−5 y |
3 |
+ y |
6 |
= −2, |
||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
yi ≥ 0, i = |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1, 6. |
|
|
|
|
|
|
||||
|
Очевидно, |
что первое базисное решение недопустимо, а |
|||||||||||||||||
коэффициенты целевой функции положительны, т.е. удовлетворяют условиям оптимальности. Роль столбцов и строк этой задачи играют соответственно строки и столбцы предыдущей. Поэтому выбор ведущего коэффициента в двойственной задаче надо выбирать, исходя из этих условий. Дополнительный комментарий приведем в конце решения.
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
св.чл. |
-5 |
-5 |
-10 |
1 |
0 |
0 |
-4 |
-8 |
-5 |
-2 |
0 |
1 |
0 |
-3 |
-4 |
-6 |
-5 |
0 |
0 |
1 |
-2 |
400 |
300 |
200 |
0 |
0 |
0 |
min |
1/2 |
1/2 |
1 |
-1/10 |
0 |
0 |
2/5 |
-7 |
-4 |
0 |
-1/5 |
1 |
0 |
-11/5 |
-3/2 |
-7/2 |
0 |
-1/2 |
0 |
1 |
0 |
300 |
200 |
0 |
20 |
0 |
0 |
-80 |
0 |
3/14 |
1 |
-4/35 |
1/14 |
0 |
17/70 |
1 |
4/7 |
0 |
1/35 |
-1/7 |
0 |
11/35 |
0 |
-37/14 |
0 |
16/35 |
-3/4 |
1 |
33/7 |
0 |
200/7 |
0 |
80/7 |
300/7 |
0 |
1220/7 |
В первом блоке таблицы |
имеем |
|
недопустимое решение |
|||||
Y1 = (0,0,0, |
-4, |
-3, -2), во втором |
блоке |
— недопустимое |
||||
решение |
Y2 = (0,0,2/5,0, -11/5,0), |
в |
третьем |
блоке |
— |
|||
допустимое решение Y3 = (11/35,0,17/70,0,0,33/7). |
При |
этом |
||||||
F(Y3) = 1220/7. |
Отбрасывая |
значения |
дополнительных |
|||||
неизвестных y4, y5 и y6, получаем |
оптимальное решение |
|||||||
|
|
|
63 |
|
|
|
|
|
двойственной задачи Yопт = (11/35,0,17/70) и соответствующий минимум Fmin = 1220/7.
Отметим принцип выбора ведущего коэффициента в двойственной задаче. Это делается по следующим правилам:
1)в качестве ведущей строки берется та, в которой имеется наибольший из модулей свободных членов системы уравнений (ограничений);
2)ведущий столбец берется, исходя из минимума модулей отношений коэффициентов индексной строки к соответствующим коэффициентам разрешающей строки.
Сравним последние блоки таблиц Гаусса в прямой и двойственной задачах. Можно заметить, что коэффициенты индексной строки в оптимальном плане прямой задачи, взятые
спротивоположными знаками, являются значениями переменных оптимального плана двойственной задачи. Коэффициенты индексной строки в оптимальном плане двойственной задачи являются значениями переменных оптимального плана прямой задачи. При этом минимальное значение целевой функции двойственной задачи равно максимальному значению целевой функции прямой задачи.
Эти совпадения соответствуют следующему сопоставлению основных и дополнительных переменных прямой и двойственной задач:
x1, x2, x3 |
x4, x5, x6 |
основные |
дополнительные |
y1, y2, y3 |
y4, y5, y6 |
дополнительные |
основные |
Таким образом, зная решение одной задачи, можно, не решая вторую задачу, найти ее решение.
464

Пример 5.5. (решение задачи примера 2.1.) Основная задача имеет вид
L(X ) = 4x1 +5x2 +6x3 → min,
2x1 +3x2 = 32,
4x1 + x2 +2x3 ≥ 40,3x1 + x2 +3x3 ≤ 50,
xj ≥ 0, j =1,3.
Решение. Поскольку прямых задач было решено много, обратимся сразу к двойственной задаче
F (Y ) = 32y1 +40y2 −50y3 → max,
2 y1 +4y2 −3y3 ≤ 4,
3y1 + y2 − y3 ≤ 5,2 y2 −3y3 ≤ 6,
y2 ≥ 0, y3 ≥ 0.
(ограничение у1 > 0 отсутствует). Положим у1 = у’1 – у’’1, вводим дополнительные переменные y4, y5, y6, приводим задачу к каноническому виду и строим рабочую таблицу Гаусса (табл. 5.2).
Отбрасывая дополнительные переменные y4, y5, y6 и определяя у1 = у’1 – у’’1 = 8/5, получаем решение двойственной задачи
Fmax(Y) = F(8/5,1/5,0) = 296/5. 65
|
|
|
|
|
|
|
Таблица 5.2 |
||
|
|
|
|
|
|
|
|
|
|
y’1 |
y’’1 |
y2 |
y3 |
y4 |
y5 |
y6 |
св.чл. |
||
2 |
-2 |
4 |
-3 |
1 |
0 |
0 |
4 |
|
|
3 |
-3 |
1 |
-1 |
0 |
1 |
0 |
5 |
|
|
0 |
2 |
-3 |
0 |
0 |
0 |
1 |
6 |
|
|
32 |
-32 |
40 |
-50 |
0 |
0 |
0 |
max |
|
|
1/2 |
-1/2 |
1 |
-3/4 |
1/4 |
0 |
0 |
1 |
|
|
5/2 |
-5/2 |
0 |
-1/4 |
-1/4 |
1 |
0 |
4 |
|
|
3/2 |
1/2 |
0 |
-9/4 |
3/4 |
0 |
1 |
9 |
|
|
12 |
-12 |
0 |
-20 |
-10 |
0 |
0 |
-40 |
|
|
0 |
0 |
1 |
-7/10 |
3/10 |
-1/5 |
0 |
1/5 |
|
|
1 |
-1 |
0 |
-1/10 |
-1/10 |
2/5 |
0 |
8/5 |
|
|
0 |
2 |
0 |
-39/20 |
9/10 |
-3/5 |
1 |
33/5 |
|
|
0 |
0 |
0 |
-94/5 |
-44/5 |
-24/5 |
0 |
-296/5 |
|
|
Имея в виду связь переменных прямой и двойственной задач, получаем
Lmin(X) = L(44/5,24/5,0) = 296/5.
Ответ: Fmax(Y) = F(8/5, 1/5, 0) = 296/5, Lmin(X) = L(44/5, 24/5, 0) = 296/5.
Вопросы для самопроверки
5.1.Можно ли для задачи ЛП, содержащей в системе ограничений неравенства разных направлений, построить двойственную задачу?
5.2.Если в основной задаче отсутствуют условия неотрицательности переменных, то какие последствия это влечет в сопряженной задаче?
5.3.Чем отличаются матрицы систем ограничений в паре двойственных задач?
66

5.4.Какова связь между экстремальными значениями пары двойственных задач ЛП?
5.5.Что можно сказать о решении двойственной задачи, если решение основной задачи не существует по причине несовместимости ее системы ограничений?
5.6.Можно ли производить симплексное преобразование, используя отрицательный разрешающий коэффициент?
5.7.Могут ли обе двойственные задачи быть задачами на максимум?
6. Транспортная задача
Постановка транспортной задачи
6.1. Имеются m пунктов отправления однородного груза А1, А2,…, Аm и n пунктов назначения того же груза В1, В2, ...,
Вn . Предполагается, что из любого пункта Аi ( i =1, m ) груз может быть доставлен в любой пункт Вj ( j =1, n ).
Обозначения:
аi > 0 — объем (запас) груза в пункте Ai ;
bj > 0 — объем груза, необходимого в пункте Bj ;
ci j > 0 — стоимость (тариф) перевозки единицы груза
из Ai в Bj .
Требуется определить план перевозок груза из пунктов Ai
впункты Bj так, чтобы:
1)вывезти весь груз от отправителей Ai ;
2)удовлетворить потребность в грузе (спрос) каждого потребителя Bj ,
3)транспортные расходы были минимальными.
Под планом задачи подразумевается матрица
67
x11 |
x12 |
... |
x1n |
|
||
x |
x |
... |
x |
|
, |
|
X = |
21 |
22 |
... |
2n |
||
... |
... |
... |
|
|
||
|
|
xm2 |
... |
|
|
|
xm1 |
xmn |
|
||||
где xi j — количество единиц груза, который необходимо перевезти из точки Ai в точку Вj .
Математическая модель сформулированной задачи, называемой транспортной задачей, имеет следующий вид:
требуется найти неотрицательную матрицу X, удовлетворяющую условиям
n |
m |
||||
∑xi j = ai (i = |
1, m |
) , |
∑xi j = a j ( j = |
1, n |
) , |
j =1 |
i =1 |
||||
и доставляющую минимум целевой функции |
|||||
|
|
n |
m |
||
L(X ) = ∑∑ci j xi j ,
j =1 i =1
где сi j · xi j — транспортные расходы по перевозке xi j единиц груза из пункта Аi в пункт Вj .
Теорема 6.1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы имело место условие баланса
m |
n |
∑ai |
= ∑b j . |
i =1 |
j =1 |
6.2. Неотрицательная матрица X, удовлетворяющая условиям задачи называется планом (или допустимым планом) задачи. Допустимый план называется оптимальным, если он
68

доставляет минимум целевой функции.
Допустимый план, имеющий не более m + n - 1 отличных от нуля компонентов хi j , называется базисным, или опорным. Опорный план, имеющий ровно m + n - 1 отличных от нуля компонент, называется невырожденным, а если число отличных от нуля компонент меньше, чем m + n - 1, то план называется вырожденным.
Прежде чем приступить к решению транспортной задачи, необходимо проверить условие теоремы 6.1. Если задача с неправильным балансом (открытая), то:
m |
n |
1) при ∑ai |
> ∑b j (спрос меньше предложения) |
i =1 |
j =1 |
необходимо ввести «фиктивного» потребителя груза:
|
m |
n |
bn +1 = ∑ai −∑b j ; |
||
|
i =1 |
j =1 |
m |
n |
|
2) при ∑ai |
< ∑b j |
(спрос больше предложения) |
i =1 |
j =1 |
|
необходимо ввести «фиктивного» поставщика груза:
n |
m |
am +1 = ∑b j −∑ai . |
|
j =1 |
i =1 |
Стоимости перевозок от «фиктивного» поставщика до всех потребителей и от любого поставщика до «фиктивного» потребителя принимаются равными нулю.
6.3. Решение задачи начинается с определения начального опорного плана. Начальный и последующие планы заносятся в распределительную таблицу, в которой заранее записываются исходные данные задачи. Таблица с внесенными пунктами отправления Аi , их запасами ai , пунктами назначения Вj , их запросами bj и тарифами аi j (i = 1,2,..., m; j = 1,2,..., n) имеет вид табл. 6.1.
69
Таблица 6.1
Bj |
B1 |
B2 |
… |
Bn |
Запас |
|
Ai |
|
|
|
|
|
|
A1 |
с11 |
с12 |
… |
с1n |
a1 |
|
A2 |
с21 |
с22 |
… |
с2n |
a2 |
|
|
… |
… |
… |
… |
… |
|
Am |
сm1 |
сm1 |
… |
сmn |
am |
|
Спрос |
b1 |
b2 |
… |
bm |
∑ai = |
∑b j |
Тарифы ci j записаны в левом верхнем углу клетки, а величины поставок xi j будут записываться в правом нижнем углу клетки.
Примечание. При введении «фиктивного» потребителя Вn + 1 (поставщика Аm+ 1 ) соответствующий столбец (строка)
заполняется нулями, т.е. ci ,n +1 = 0 (cm+ 1 ,j = 0).
Начальный план составляется методом минимальных тарифов, который заключается в следующем. Выбирается наименьший тариф, скажем, ci j . В клетке (i,j) этого тарифа (в правом нижнем углу) записывается максимально возможная поставка с учетом ограничений этой строки и этого столбца: хi j = min(аi ,bj ). Этой поставкой либо обеспечивается потребность одного потребителя, и тогда этот потребитель (столбец) исключается из дальнейшего рассмотрения, либо от одного поставщика забирается весь груз, и тогда этот поставщик (строка) исключается из дальнейшего рассмотрения. Исключаемый столбец (или строка) нумеруется, и этот номер записывается на краю этого столбца (или строки). Исключаемые одновременно строка и столбец отмечаются одним номером.
Если имеются два или более одинаковых наименьших тарифов, то заполняемая клетка берется произвольно среди них.
Описанная операция повторяется до тех пор, пока не будут
70

зачеркнуты все столбцы и строки. На последнем шаге одновременно освобождаются строка и столбец, а следовательно, в благоприятном случае должно быть m + n – 1 заполненных клеток. Полученный план является невырожденным.
Примечание. При одновременном зачеркивании строки и столбца (кроме последнего шага) число заполненных клеток меньше, чем m + n – 1, и такой план является вырожденным. Его надо дополнить до невырожденного плана нулями: нули надо записать в клетки, расположенные в строке или в столбце, которые одновременно исключены из рассмотрения, т.е. имеют один номер. При этом, клетки, заполненные нулями, не должны составлять цикл с прочими заполненными клетками (понятие цикла см. ниже).
Подчеркнем, что начальный план записывается в распределительной (первоначальной) таблице, и соответствующие поставки отделяются уголками для зрительного контраста.
В таблицах 6.2 и 6.3 показаны примеры невырожденного и вырожденного планов (в обеих таблицах m = 3, n = 4, m + n – 1 = 6; при этом на дополнительные строку и столбец обращать
внимание не следует – о них позже). |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Таблица 6.2 |
|
|
|
1) |
2) |
6) |
5) |
|
|
||||
3) |
|
70 |
60 |
80 |
70 |
ui |
|
||||
90 |
1 |
|
5 |
|
6 |
|
1 |
|
0 |
|
|
4) |
|
|
70 |
|
|
|
|
|
20 |
|
|
100 |
4 |
|
1 |
|
3 |
|
4 |
|
3 |
|
|
5) |
|
|
|
|
60 |
|
|
|
40 |
|
|
90 |
3 |
|
3 |
|
5 |
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
80 |
|
10 |
|
|
|
vj |
1 |
-2 |
|
2 |
|
1 |
|
|
||
|
|
|
|
|
|
71 |
|
|
|
|
|
Число положительных компонент начального плана равно m + n – 1 = 6,
следовательно, план невырожденный.
Таблица 6.3
|
|
1) |
2) |
5) |
4) |
|
||||
3) |
|
70 |
60 |
80 |
70 |
|
||||
90 |
1 |
|
5 |
|
6 |
|
1 |
|
|
|
4) |
|
|
70 |
|
|
|
|
|
20 |
|
100 |
4 |
|
1 |
|
3 |
|
4 |
|
|
|
5) |
|
|
* |
|
60 |
|
* |
|
50 |
|
80 |
3 |
|
3 |
|
5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
80 |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
Число положительных компонент начального плана равно пяти. При заполнении таблицы одновременно зачеркнуты вторая строка и четвертый столбец. План вырожденный. Отмеченная уголком и звездочкой клетка должна заполняться нулем (о роли звездочек см. ниже в п. 6.5).
6.4. После получения первого (начального) плана следует
n m
определить стоимость его реализации: L(X ) = ∑∑ci j xi j .
j =1 i =1
Затем план проверяется на оптимальность методом потенциалов, который заключается в следующем. Потенциалами данного плана называется набор из m + n
действительных чисел ui ( i =1, m ) и vj ( j =1, n ),
удовлетворяющих условиям: ui + vj = ci j , где сi j – тариф занятой клетки. Поскольку число занятых клеток равно m + n – 1, то для однозначного определения потенциалов один из них можно брать произвольно, например, u1 = 0. Потенциалы записываются в дополнительных строке и столбце. Как правило, потенциалы определяются в уме. Именно эти потенциалы занесены в табл. 6.2. Здесь мы приняли u1 = 0.
72
Остальные |
потенциалы |
находятся |
последовательно |
|||
следующим образом: |
|
|
|
|||
u1 + v1 |
= c1 1 = 1 (v1 |
= 1, так как u1 |
= 0); |
|||
u1 |
+ v4 = c1 4 |
= 1 (v4 |
= 1); |
|
||
u3 |
+ v4 = c3 4 |
= 4 |
(v3 |
= 3); |
|
|
u3 |
+ v3 |
= c3 3 |
= 5 |
(v3 |
= 2); |
|
u2 |
+ v2 |
= c2 2 |
= 1 (v2 |
= -2). |
|
|
Полученная система потенциалов позволяет проверить полученный план на оптимальность. Составляем разности i j = сi j - ui - vj , для всех клеток таблицы. Поскольку для занятых клеток i j = 0 (по определению), то остается найти i j , для незанятых клеток. Эти величины (числа) называются оценками клеток распределительной таблицы, или плана.
Теорема 6.2 (теорема оптимальности). Опорный план X оптимален в том и только в том случае, если среди оценок i j этого плана нет отрицательных.
Если среди оценок i j есть отрицательные, то план неоптимален и его улучшают методом перераспределения поставок по циклу. Отметим клетку с наименьшей отрицательной оценкой и построим цикл с начальной вершиной в этой клетке.
6.5. Циклом с начальной вершиной в данной клетке называется замкнутая ломаная, обладающая следующими свойствами:
1) все ее вершины, кроме начальной, расположены
взанятых клетках;
2)звенья (стороны) цикла расположены в строках и столбцах таблицы;
3)в каждой вершине звенья соединяются под прямым
углом;
4)на звеньях цикла могут быть занятые клетки, но они не являются вершинами цикла;
5)два звена могут пересекаться в какой-либо клетке, но
73
эта клетка не должна быть занятой (иначе она является вершиной).
Примечание. Свойства 4 и 5 обеспечивают некоторую минимальность цикла: он не должен распадаться на объединение двух или более меньших циклов.
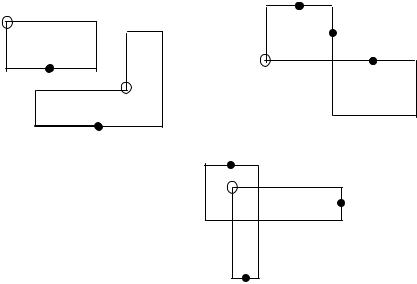
На рис. 6.1 изображено несколько циклов с началом в незанятой клетке (именно такие циклы встречаются при исследовании плана на оптимальность). Приняты обозначения: О — незанятая клетка (начало цикла), * — занятая клетка; возможные места расположения занятых клеток отмечены черным кружком на звеньях.
* |
|
* |
* |
|
* |
* |
|
|
|
|
|
|
||
* |
|
|
|
* |
|
|
|
|
|
* |
|
|
* |
|
* |
|
* |
* |
|
|
|
|
||
|
|
* |
|
* |
|
|
|
|
|
|
|
* |
|
* |
* *
Рис. 6.1
На рис. 6.2 изображено несколько замкнутых ломаных, не являющихся циклами: «так нельзя». Штриховыми линиями обозначены возможности сокращения цикла или распада
74
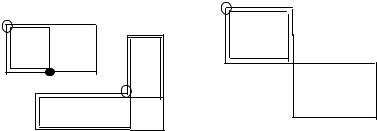
цикла на объединение (сумму) нескольких циклов. Рис. 6.2 показывает, что в цикл нельзя вовлекать «больше, чем надо» клеток.
*
* |
* |
* |
* |
|
|
* |
|
* |
* |
* |
|
|
|
|
|
||
* |
|
* |
* |
* |
|
* |
* |
* |
|||
|
|
Рис. 6.2
Примечание. Вспомним случай вырожденного плана и обратимся к таблице 6.3. Для того чтобы план стал невырожденным, надо занять одну клетку нулем (иначе нельзя определить потенциалы, а значит, нельзя проверить на оптимальность полученный план). Нуль можно записать либо в строке i = 2, либо в столбце j = 4, ибо они были исключены одновременно в четвертую очередь (именно для этого была нужна нумерация исключаемых строк и столбцов). В клетке (2,1), которая отмечена звездочкой, записать нуль нельзя: эта клетка образует цикл с занятыми клетками (1,1), (1,4) и (2,4). Можно было занимать либо клетку (3,4), либо (2,3), которые тоже отмечены звездочками. Последняя клетка и была занята и отмечена уголком, хотя в качестве занятой можно было бы брать и клетку (3,4).
6.6.Итак, построен цикл с вершиной в отмеченной клетке
снаименьшей отрицательной оценкой. Если таких клеток несколько, то следует брать одну из них произвольно, или клетку с меньшим тарифом. В любом порядке перенумеруем вершины цикла. Тем самым вершины разбиваются на две
75
группы — с нечетными (отмеченная считается первой, т.е. нечетной) и четными номерами. Найдем наименьшую из величин поставок четных вершин (обозначим ее буквой θ). Эту величину прибавим ко всем вершинам с нечетными номерами
иотнимем от вершин с четными номерами. Новое распределение поставок присоединяется к остальным занятым
клеткам; таким образом, составляется новый опорный план Х2 с L(Х2) < L(Х1). Этот план заносится в новую таблицу и проверяется на оптимальность методом потенциалов. В новой
таблице необязательно записывать величины аi и bj . Улучшение новых планов проводят до тех пор, пока
очередной план не станет оптимальным. Для него все оценки клеток должны быть неотрицательными. Цикл и перераспределение поставок рекомендуется выносить за таблицу, т.е. рассматривать их отдельно. При заполнении клеток тарифами, поставками, оценками рекомендуется для контраста использовать разные цвета, а цикл в таблице выделять отдельным цветом и штриховой линией.
Пример 6.1. Решить транспортную задачу по данным табл. 6.2.
Решение. Перепишем здесь табл. 6.2, опуская величины ai
иbj При этом буквы ui , vj , - перенесем в правый нижний угол расширенной таблицы (табл. 6.4).
1)Проверяем составленный план, взятый из табл. 6.4 (заметим, что он составлен из поставок, записанных в правом нижнем углу клеток и отмеченных уголком), на оптимальность, вычисляя оценки всех клеток таблицы.
|
|
70 |
0 |
0 |
30 |
|
X1 |
|
0 |
60 |
0 |
40 |
|
= |
|
|||||
|
|
0 |
0 |
80 |
10 |
|
|
|
|
||||
|
|
|
76 |
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.4 |
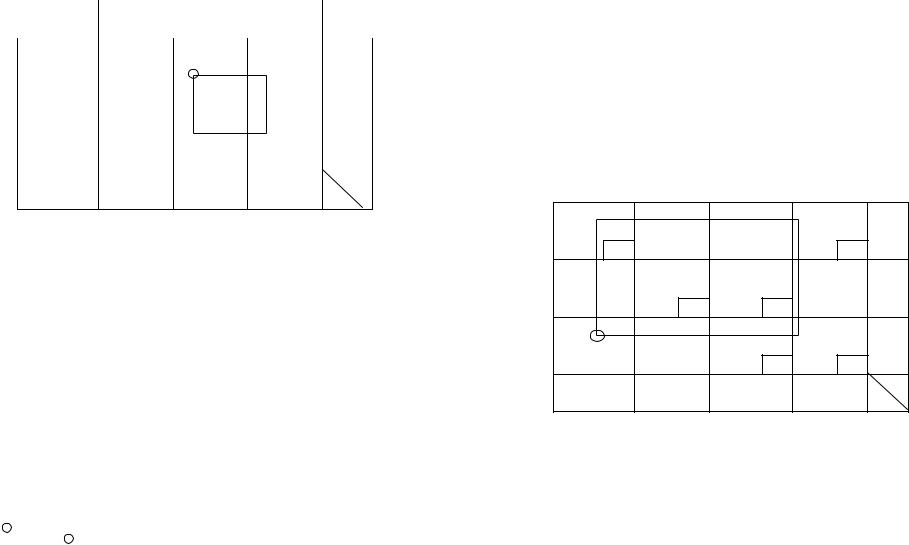
L(X1) = 70·1 + 20·1 + 60·1 + 40·4 + 80·5 + 10·4 = 750 (ден. ед.). |
||
|
|
|
|
|
|
|
|
2) Строим цикл |
с началом в отмеченной клетке |
||
|
|
|
|
|
|
|
|
|
|
(2,3) с минимальной |
оценкой 23 = - 2. |
1 |
5 |
|
6 |
|
1 |
|
|
|
Для его пересчета выносим цикл отдельно. Минимальная |
||
0 |
7 |
|
4 |
|
0 |
0 |
|
поставка по четным вершинам равна θ = 40. Эту величину |
|||
|
70 |
|
|
|
|
|
20 |
|
|
вычтем из вершин с четными номерами и прибавим к |
|
4 |
1 |
3 |
|
4 |
|
|
|
вершинам с нечетными номерами. Старые поставки записаны |
|||
0 |
0 |
-2 |
|
0 |
3 |
|
вне цикла, а новые — внутри него. Клетка (2,3) была |
||||
|
|
|
60 |
|
|
|
40 |
|
|
свободной, сейчас стала свободной клетка (2,4). |
|
|
|
|
|
|
|
|
|
3) Строим новую таблицу (табл. 6.5), в которую заносим |
|||
3 |
3 |
5 |
|
4 |
|
|
|
||||
-1 |
2 |
0 |
|
0 |
3 |
|
новый план, состоящий из старых поставок, не вовлеченных в |
||||
|
|
|
|
|
|
|
|
|
|
цикл, и новых — в вершинах рассмотренного цикла. |
|
|
|
|
|
|
80 |
|
10 |
|
|
||
|
|
|
|
|
|
|
|
Таблица 6.5 |
|||
|
|
|
|
|
|
|
|
ui |
|
||
|
|
|
|
|
|
|
|
|
|
||
1 |
-2 |
2 |
1 |
vj |
1 |
5 |
6 |
|
1 |
|
|
|
|
|
|
|
0 |
||||
|
|
|
|
|
0 |
5 |
|
4 |
0 |
|
Для этого оценки |
ij = ci j – ui – vj , равные нулю для занятых |
|
70 |
|
|
|
20 |
|||
4 |
1 |
3 |
|
4 |
|
|||||
клеток, вычислим для всех незанятых клеток и результаты |
|
1 |
||||||||
запишем в центре клетки. Эти оценки уже занесены в таблицу, |
2 |
0 |
40 |
0 |
2 |
|||||
а теперь укажем способ их получения (конечно, это надо |
|
60 |
|
|
40 |
|
||||
делать в уме): |
|
|
|
|
3 |
3 |
5 |
|
4 |
3 |
12 = c12 – u1 – v2 = 5 – 0 + 2 = 7, |
|
|
-1 |
0 |
|
0 |
0 |
|||
13 = c13 – u1 – v3 = 6 – 0 – 2 = 4, |
|
|
|
|
|
|
40 |
50 |
||
21 = c21 – u2 – v1 = 4 – 3 – 1 = 0, |
|
|
1 |
0 |
|
-2 |
1 |
ui |
||
23 = c23 – u2 – v3 = 3 – 2 – 3 = – 2 < 0 (!), |
|
|
vj |
|||||||
31 = c31 – u3 – v1 = 3 – 1 – 3 = -1 < 0 (!), |
|
|
|
|
|
|
|
|||
32 = c32 – u3 – v2 = 3 – 3 + 2 = 2. |
|
|
Этот план имеет вид |
|
|
|
|
|||
Подчеркнем, что если (i, j) – занятая клетка, то i j = 0.
|
|
Получили две клетки с отрицательным оценками: |
|||||
I |
|
|
IV |
|
31 = -1, |
23 = -2. |
|
|
|
|
|
План |
неоптимален, |
будем его |
|
|
40 |
|
40 |
||||
|
40 |
50 |
10 |
улучшать. |
Но прежде |
определим |
|
80 |
стоимость реализации этого плана: |
||||||
|
|
|
|||||
II |
|
|
III |
||||
|
|
|
77 |
|
|||
|
|
|
|
|
|
||
|
|
70 |
0 |
0 |
20 |
|
|
X 2 |
|
0 |
60 |
40 |
0 |
|
, |
= |
|
||||||
|
|
0 |
0 |
40 |
50 |
|
|
|
|
|
|
и его стоимость равна
F(Х2) = 70 • 1 + 20 • 1 + 60 • 1 + 40 • 3 + 40 • 5 + 50 • 4 = 670 (ден. ед.). 78
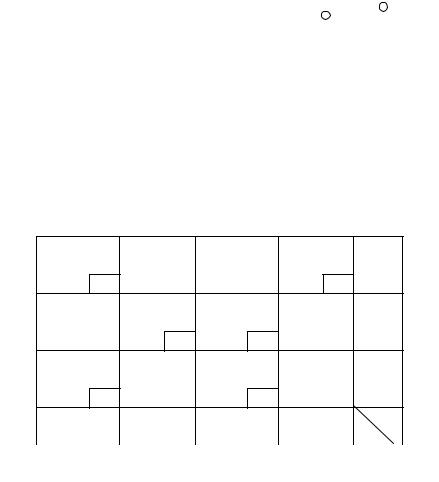
В таблицу 6.5 помещены также новые потенциалы,
найденные при условии u1 = 0. |
|
II |
|
|
Определим оценки всех клеток (хотя |
|
|
III |
|
на самом деле они также присутствуют в |
|
20 |
70 |
20 |
|
|
|
|
|
таблице). Наличие одной отрицательной |
|
50 |
|
50 |
оценки 3 1 = - 1 означает, что этот новый |
I |
|
|
IV |
план еще не оптимальный. Замкнутый |
|
|
|
|
цикл с вершиной в клетке (3,1) также отмечен в таблице 6.5. Его пересчет произведем отдельно.
На этот раз перераспределяем поставку в θ = 50, это приводит к поставкам, обозначенным внутри цикла.
4) Составляем новый план, заносим его в новую таблицу (табл. 6.6), опять определяем новые потенциалы, новые оценки и делаем вывод об оптимальности.
|
|
|
|
|
Таблица 6.6 |
1 |
5 |
6 |
|
1 |
0 |
0 |
4 |
|
3 |
0 |
|
|
20 |
|
|
|
70 |
4 |
1 |
3 |
|
4 |
0 |
3 |
0 |
40 |
0 |
3 |
|
|
3 |
60 |
|
40 |
|
3 |
5 |
|
4 |
-2 |
|
50 |
0 |
|
0 |
1 |
|
|
50 |
|
|
40 |
ui |
- 1 |
- 1 |
|
- 3 |
- 1 |
|
|
vj |
||||
Отрицательных оценок нет: план оптимален. Его стоимость |
|||||
равна |
|
|
|
|
|
L(Х2) = 20 + 70 + 60 + 120 + 150 + 200 = 620 (ден. ед.). |
|||||
|
|
|
|
79 |
|
Ответ:
|
|
20 |
0 |
0 |
80 |
|
|
|
X3 |
|
0 |
60 |
40 |
0 |
|
, |
|
= |
|
L(X3) = 620. |
||||||
|
|
50 |
0 |
40 |
0 |
|
|
|
|
|
|
|
|
Задача решена.
Примечание 1. Визуально проанализируйте этот план, сравните его с начальным и обнаружите преимущества оптимального плана.
Примечание 2. При пересчете стоимости нового плана можно ограничиться пересчетом только тех поставок, которые участвовали в цикле. Экономия на цикле переносится на весь план. Это важно, когда задачи, а значит, и таблицы, громоздкие. Иногда в цикл может быть вовлечена значительная часть заполненных клеток.
Пример 6.2. Решить задачу, заданную табл. 6.3.
Решение. Перепишем здесь эту таблицу с клеткой (2,3), заполненной нулем (табл. 6.7). Занятая клетка нужна для того, чтобы можно было определить потенциалы. Потенциалы определяем в уме и заносим в эту же таблицу:
u1 = 0, u1 + v4 = 1 → v1 = 1, v4 + u2 = 3 → u2 = 2,
u2 + v2 = 1 → v2 = -1, u1 + v1 = 1 → v1 = 1, u2 + v3 = 4 → v3 = 2, v3 + u3 = 5 → u3 = 3.
80
