
Спецглавы высшей математики: методы оптимизации. Пантелеев И.Н
.pdf
» output.firstorderopt ans =
7.9822e-010
Данные результаты говорят об успешном решении задачи. Команда spy(Hstr) позволяет графически представить структуру разреженной матрицы (рис. 4).
Рис.4. Структура разреженной матрицы Hstr
2.11. Нелинейная минимизация с ограничениями в виде линейных равенств
Продолжим рассмотрение задачи с минимизацией введенной функции, добавив в нее ограничения в виде100 линейных равенств
Aeq х = beq,
181
то есть матрица Aeq имеет размер 100x1000. |
|
|
|||
Будем |
полагать, |
что матрица Aeq |
и вектор beq |
|
|
содержатся в файле browneq.mat. |
|
|
|
||
Этап 1. В |
данном |
случае |
будем |
использовать |
ранее |
подготовленный m-файл brownfgh. |
|
|
|
||
Этап 2. Составление программы для поиска решения: |
|
||||
»fun = 'brownfgh';
»load browneq % Загрузка матрицы Aeq и вектора beq
»n = 1000;
» xstart = -ones(n,l); xstart(2:2:n) = 1; % Начальные значения
»options = optimset('GradObj', 'on', 'Hessian','on', ...
'PrecondBandWidth', inf);
»% Поиск решения
»[x, fval, exitflag, output] = ...
fmincon('brownfgh', xstart, [], [], Aeq, beq, [], [], [], options);
Результаты расчета предст удовлетворительными (об этом можно судить, например, но
величине нормы невязки norm(Aeq*x-beq)):
»exitflag exitflag =
1
»fval fval =
205.9313
»output output =
iterations: 16 funcCount: 16 cgiterations: 14
firstorderopt: 2.1434e-004
algorithm: 'large-scale: projected trust-region Newton' The linear equalities are satisfied at x norm(Aeq*x-beq)
ans =
1.1913е-012 182

|
2.12. Задача квадратичного программирования |
|
|
||
Для |
минимизации |
квадратичной |
формы, зависящей |
от |
|
большого числа переменных, следует использовать функцию |
|||||
quadprog. Рассмотрим |
подобную |
задачу |
при |
числе |
|
переменных 400 и симметричной трех-диагональной матрице Н, сохраненной в файле qpboxl.mat.
Соответствующая программа и результаты вычислений приведены ниже.
»load qpboxl % Загрузка матрицы Н
»% Задание граничных значений
»lb = zeros(400,1); lb(400) = -inf;
»ub = 0.9*ones(400,1); ub(400) = inf;
»f = zeros(400,1); f([l 400]) = -2;
»xstart = 0.5*ones(400,1); % Начальные значения
»% Поиск решения
»[х, fval, exitflag, output] = ...
quadprog(H, f, [], [], [], [], lb, ub, xstart);
»exitflag exitflag =
1
»output output =
firstorderopt: 7.8435e-006 iterations: 20 cgiterations: 1809
algorithm: 'large-scale: reflective trust-region'
2.13. Решение задачи линейного программирования
Рассмотрим |
задачу |
линейного |
программирования |
в общем |
||||
виде (см. табл. |
1), |
полагая, что |
все |
исходные |
данные |
|||
содержатся |
в |
|
файлеsc50b.mat. |
Задача |
включает48 |
|||
переменных, |
30 |
неравенств и20 |
равенств, |
так |
что |
вполне |
||
может |
быть |
отнесена |
к |
задачам |
большой |
мерности. |
|
|
функцииlinprog |
|
|
Текст |
программы |
с использованием |
и |
||
полученные результаты приведены ниже: |
|
|
|||
»load sc50b
»[х, fval, exitflag, output] = ...
linprog(f, A, b, Aeq, beq, lb, [], [], optimset('Display'.'iter')):
Residuals: |
Primal |
|
Dual |
|
Duality |
Total |
|
|
|
Infeas |
|
Infeas |
|
Gap |
Rel |
|
|
A*x-b |
|
A'*y+z-f |
|
x'*z |
Error |
Iter |
0: |
1.50e+003 |
|
2.19e+00 |
|
1.91e+004 |
1.00e+00 |
Iter |
1: |
1.15e+002 |
|
2.94e-015 |
|
3.62e+003 |
9.90e-001 |
Iter |
2: |
1.16e-012 |
|
2.21e-015 |
|
4.32e+002 |
9.48e-001 |
Iter |
3: |
3.23e-012 |
|
5.16e-015 |
|
7.78e+001 |
6.88e-001 |
Iter |
4: |
5.78e-011 |
|
7.61e-016 |
|
2.38e+001 |
.69e-001 |
Iter |
5: |
9.31e-011 |
|
1.84e-015 |
|
5.05e+000 |
6.89e-002 |
Iter |
6: |
2.96e-011 |
|
1.62e-016 |
|
1.64e-001 |
2.34e-003 |
Iter |
7: |
1.51e-011 |
|
2.74e-016 |
|
1.09e-005 |
1.55e-007 |
Iter |
8: |
.51e-012 |
|
.37e-016 |
|
1.09e-011 |
1.51e-013 |
Optimization terminated successfully.
»exitflag exitflag =
1
»fval fval =
-70.0000
»output output =
iterations: 8 cgiterations: 0 algorithm: 'lipsoV
184
183
Заключение
Учебное пособие представляет интерес для студентов,
изучающих один |
из |
важных разделов |
спецглав |
высшей |
|||
математики - методы оптимизации. |
|
|
|
|
|||
Структура первой |
части |
пособия позволяет |
обойтись |
||||
без дополнительного учебника, если речь идет о решении |
|||||||
практических |
задач |
по |
линейному |
программированию. |
|||
Каждый из восьми параграфов содержит краткую и вместе с |
|||||||
тем достаточную теоретическую информацию, приведены все |
|||||||
«работающие» |
теоремы |
и |
утверждения, позволяющие |
||||
приступить к решению соответствующих задач. Графический |
|||||||
(геометрический) |
метод |
решения |
задач |
|
излагается |
||
традиционно. Что касается наиболее значимого «симплексного |
|||||||
метода», то |
тут |
изложение |
материала |
проведено |
более |
||
экономным, методически оправданным способом. |
|
|
|||||
Вторая |
и |
третья |
части |
пособия |
дают |
возможность |
|
познакомиться с методами решения практических задач
оптимизации |
(планирования |
комплекса |
работ, |
нахождения |
|||
кратчайшего пути, определения максимального потока, задача |
|||||||
замены |
оборудования |
и .)др. Краткий |
обзор |
приложений |
|||
пакета |
MatLab |
дает |
представление |
о |
разнообразных |
||
возможностях использования этой системы на практике. |
|||||||
Пособие может быть использовано студентами для |
|||||||
подготовки |
к |
практическим |
занятиям |
и |
при выполнении |
||
курсовой работы.
185
Библиографический список
1.Акулич И. Л. Математическое программирование в примерах и задачах.-M: Высш. шк, 1986.-320 с.
2.Ашманов С.А., Тимохов А.В. Теория оптимизации в задачах
и упражнениях.- M.: Наука, 1991.- 448 с.
3.Банди Б. Основы линейного программирования. - M: Радио и связь, 1989.-176 с.
4.Банди Б. Методы оптимизации. Вводный курс.- М.: Радио и связь, 1988.- 128 с.
5.Калихман И. Л. Сборник задач по математическому программированию.-M: Высш. шк, 1975.-261 с.
6.Ногин В.Д., Протодьяконов И.О., Евлампиев И.И. Основы теории оптимизации.: Учеб. пособие для студентов втузов: -
М.: Высш. школа, 1986. – 384 с.
7.Таха Х. Введение в исследования операций. Т.1. – М.: Мир, 1985. – 480 с.
8.Триус Е.Б. Задача математического программирования транспортного типа. – Киев: Вища школа, 1983. – 659 с.
9.Трифонов А.Г. Постановка задачи оптимизации и численные методы ее решения: Учебник. – М.: 2002. – 115 с.
10.Дьяконов .В, Круглов .В Математические пакеты расширения MATLAB. Специальный справочник.- СПб.:
Питер, 2001.-480 с.
11.Зуховицкий Л.И., Авдеев С.И. Линейное и выпуклое программирование. - M.: Наука, 1994.
186
Приложение
З а д а ч а л и н е й н о г о п р о г р а м м и р о в а н и я ( З ЛП )
П о с т а н о в к а к а н о н и ч е с к о й з а д а ч и :
Решается задача:
n
f (x) = åC j x j ® max
j =1 |
|
|
n |
|
|
åai j x j = bi , |
i =1...m < n |
(1) |
j =1 |
|
|
x j ³ 0, |
j =1...n |
|
П о с т а н о в к а о с н о в н о й з а д а ч и :
Решается задача:
n
f (x) = åC j x j ® max
j =1 |
|
|
n |
|
|
åai j x j |
£ (³) bi , i =1...m < n |
(2) |
j =1 |
|
|
x j ³ 0, |
j =1...n |
|
П о с т а н о в к а о б щ е й з а д а ч и :
Решается задача:
187
n |
|
|
|
f (x) = åC j x j |
® max |
|
|
j =1 |
|
|
|
n |
|
|
|
åai j x j |
= bi , |
i =1...k |
|
j =1 |
|
|
|
n |
|
|
|
åai j x j |
£ (³) bi , |
i = k +1...m < n |
(3) |
j =1 |
|
|
|
x j ³ 0, |
|
j =1...n |
|
О б щ а я х а р а к т е р и с т и к а п о с т а в л е н н ы х з а д а ч
1.Решается задача поиска максимума целевой функции
2.Максимизируемая функция и ограничения линейны по xj
3 . Задачи содержат ограничения на знак переменныхxj . Если по физической постановке какая-либо переменная, вляется неограниченной по знаку, её всегда можно представить в виде
xj = xn + 1 – xn + 2 , где xn + 1 ≥ 0 , xn + 2 ≥ 0
В случае двух переменных, поставленные задачи могут быть решены графически.
Алгоритм графического решения задачи
1. |
Построить |
множество допустимых значений, задаваемое |
|
|||||||
ограничениями. |
|
|
|
|
|
|
|
|||
2. |
Построить |
градиент |
целевой |
функции |
в |
точке |
с |
|||
координатами (0,0). |
|
|
|
|
|
|
|
|||
3. |
Построить |
линию уровня целевой функции, проходящую |
|
|||||||
через точку с координатами (0,0). |
|
|
|
|
|
|||||
4. |
Если |
требуется |
найти |
максимум |
целевой |
функции, |
|
|||
мысленно |
|
переносить |
построенную |
линию |
|
уровня |
в |
|||
направлении градиента до последнего касания с множеством |
|
|||||||||
допустимых решений. Точка касания – максимум. |
|
|
|
|||||||
|
|
|
|
|
188 |
|
|
|
|
|

Если требуется найти минимум целевой функции, мысленно |
Т а б л и ч н ы й с и м п л е к с м е т о д Д а н ц и г а |
|||||
переносить |
построенную |
линию |
уровня |
в |
направлении |
|
градиента до первого касания с |
множеством |
допустимых |
Решение задач на основании стратегии симплекс метода |
|||
решений. Точка касания – минимум. |
|
|
|
наглядно представляется в виде таблиц специального вида. |
||
При графическом решении задачи возможны следующие |
|
|||||
варианты: |
|
|
|
|
|
|
Вслучае А - решение единственное (точка А).
Вслучае B - бесконечное множество решений (отрезок [А,B]).
В |
случае С - |
решений |
нет, |
так |
как |
область допустимых |
решений в направлении поиска решений не замкнута. |
||||||
В |
случае D – |
решений |
нет, |
так |
как |
ограничения в задаче |
несовместны. |
|
|
|
|
|
|
|
|
|
|
189 |
|
|
Алгоритм симплекс-метода |
|
|
|
|
||
Замечание |
№1. При решении задачи симплекс-методом |
|||||
ограничения |
на знак |
переменных не |
участвуют |
ни в |
||
подготовке задачи к решению, ни в самом счете. |
|
|
||||
Решение задачи симплекс методом включает два |
этапа: |
|||||
этап подготовки задачи к решению и этап вычислений. |
|
|||||
Этап подготовки задачи к решению |
|
|
||||
1. Симплекс-метод |
ищет |
максимум |
функции. Если |
|||
требуется найти минимум, |
умножить целевую функцию на |
|||||
(-1) и перейти к задаче поиска максимума. |
|
|
||||
2. Правые |
части |
ограничений |
должны |
быть 0.≥ Если |
||
правая часть ограничения < 0, умножить его левую и правую
190

части |
на (-1) |
и |
изменить |
знак |
|
ограничения |
на |
Переменная, которой соответствует в столбце максимальная |
|||||||||||||||||||
противоположный. |
|
|
|
|
|
|
|
|
|
|
положительная |
симплекс-разность, |
вводится |
в |
базис. |
||||||||||||
3. Привести |
задачу к |
каноническому видуперейти |
от |
|
Соответствующий столбец пометим - Z. |
|
|
|
|
|
|||||||||||||||||
задачи |
с |
ограничениями |
типа |
неравенств |
к |
задаче |
с |
|
|
|
|
|
|
|
|
БP |
|
|
|
|
|||||||
ограничениями типа равенств, вводя, если это необходимо, |
|
3. Высчитать величины ri |
по формуле: ri = |
i |
|
|
|
|
|||||||||||||||||||
|
Z i |
|
|
|
|||||||||||||||||||||||
дополнительные |
|
переменные. Ввести |
|
дополнительные |
|
Переменная, |
которой |
|
соответствует |
|
|
в |
|
строке |
|||||||||||||
переменные в целевую функцию с коэффициентами равными 0. |
|
|
ri |
|
|
||||||||||||||||||||||
|
минимальная |
неотрицательная |
величина |
, |
выводится из |
||||||||||||||||||||||
4. Выписать |
столбцы |
коэффициентов |
при |
переменных в |
|
||||||||||||||||||||||
|
базиса. Соответствующую |
строку |
пометим- |
Z. |
Элемент, |
||||||||||||||||||||||
ограничениях. Если |
среди |
выписанных |
столбцов |
имеетсяm |
|
||||||||||||||||||||||
(по числу ограничений) базисных |
столбцов - |
столбцов |
|
стоящий на пересечении Z-столбца и Z -строки - разрешающий |
|||||||||||||||||||||||
единичной матрицы размерности m x m, перейти к п. 6. |
|
|
элемент - R . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5. Если |
нужное |
число базисных столбцов не найдено |
|
4. Построить новую таблицу, пересчитав предыдущую. |
|
||||||||||||||||||||||
перейти к решению М-задачи: |
|
|
|
|
|
|
|
|
|
|
|
П е р е с ч е т т а б л и ц ы |
|
|
|
|
|
||||||||||
5.1 . дописать недостающие столбцы искусственно; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
5.2. поставить |
им |
в |
соответствие |
|
искусственные |
4.1. Заполнить |
в |
новой |
таблице: строку |
коэффициентов |
|||||||||||||||||
переменные; |
|
|
|
|
|
|
|
|
|
|
|
|
функции, столбец Б п |
и столбец С i Б . |
|
|
|
|
|
|
|||||||
5.3. переписать |
ограничения |
с учетом |
искусственных |
|
4.2. Пересчитать |
|
Z-строку, |
содержащую |
|
разрешающий |
|||||||||||||||||
переменных; |
|
|
|
|
|
|
|
|
|
|
|
|
элемент и записать в новую таблицу под тем же номером: |
||||||||||||||
5.4. ввести искусственные переменные в целевую функцию |
|
новая строка = старая строка / R. |
|
|
|
|
|
|
|||||||||||||||||||
с коэффициентами равными (-М) , где М - большое |
|
Полученная строка - разрешающая. |
|
|
|
|
|
|
|||||||||||||||||||
положительное число. |
|
|
|
|
|
|
|
|
|
4.3. Пересчитать все остальные строки таблицы и записать |
|||||||||||||||||
6. Выписать |
переменные |
при |
базисных |
столбцахэти |
|
их под теми же номерами в новую таблицу: |
|
|
|
|
|
||||||||||||||||
переменные базисные. Записать начальное базисное решение: |
|
новая строка К= старая строка К −(разрешающая |
|||||||||||||||||||||||||
базисные |
переменные равны правым частям ограничений, |
в |
|
строка) * Коэффициент Пересчета, |
|
|
|
|
|
|
|||||||||||||||||
которые они входят, все остальные переменные равны 0. |
|
|
здесь |
Коэффициент |
Пересчета- |
элемент, |
стоящий на |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пересечении строки К и Z-столбца в старой таблице. |
|
|
|||||||||||
Э т а п в ы ч и с л е н и й |
|
|
|
|
|
|
|
|
|
5. Повторить |
процедуру 2-4 |
до тех пор, пока |
|
все |
симплекс- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разности не станут < 0, тогда последнее базисное решение есть |
|||||||||||||
Алгоритм |
|
|
|
|
|
|
|
|
|
|
|
решение задачи. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание №2. Если в процессе решения оказалось, что в |
|||||||||||||
1. Составить таблицу №1. |
|
|
|
|
|
|
|
|
|
базис вводится некоторая переменная(существует симплекс- |
|||||||||||||||||
2. Выписать базисное решение. Вычислить симплекс-разности |
|
разность > |
0), |
а |
|
среди |
величин r i |
нет |
ни |
одной |
|||||||||||||||||
для небазисных переменных по формуле: |
|
|
|
|
|
|
неотрицательной, значит, задача не имеет решения вследствие |
||||||||||||||||||||
|
|
|
|
D j |
= C j |
- Ci Б × Aj |
|
|
|
|
|
|
не замкнутости области допустимых решений. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
192 |
|
|
|
|
|
|
191
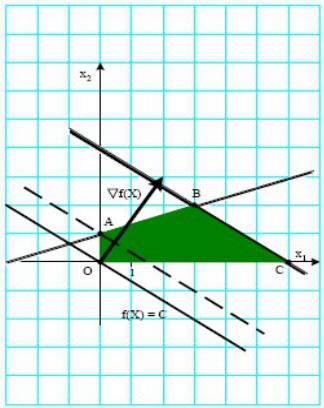
|
Замечание |
№3. |
Если |
в |
таблице, соответствующей |
следовательно |
задача |
имеет |
бесконечное множество |
|
решению задачи, в строке симплекс-разностей содержится0 |
решений на отрезке [В, С], здесь B = (3, 2), C = (6, 0). |
|||||||||
больше, чем число ограничений в задаче, значит, задача имеет |
|
|
|
|
||||||
бесконечное множество решений, одно из которых найдено. |
|
|
|
|
||||||
|
Замечание №4. Если при решении М-задачи найдено |
|
|
|
||||||
решение (все симплекс-разности < 0), но в составе базисных |
|
|
|
|
||||||
переменных осталась искусственная переменная не равная0, |
|
|
|
|
||||||
то |
исходная |
|
задача |
не |
имеет |
решения |
вследствие |
|
|
|
несовместности ограничений. |
|
|
|
|
|
|
|
|||
|
Пример 1. Дано: |
|
|
|
|
|
|
|
|
|
|
f (x) = 2x1 + 3x2 ® max |
|
|
|
|
|
|
|
||
2x1 + 3x2 £12
-2x1 + 6x2 £ 6 x1 ³ 0, x2 ³ 0
Решить задачу графически и симплекс-методом.
Г р а ф и ч е с к о е р е ш е н и е з а д а ч и
1. Множество допустимых решений (МДР), определяемое ограничениями, выделено на чертеже штриховкой.
2. |
æ 2 |
ö |
, на чертеже это вектор с |
Градиент функции: Df (x) = ç |
÷ |
||
|
è 3 |
ø |
|
началом в точке (0, 0) и концом в точке (2, 3). |
|||
3. |
Уравнение линии уровня функции: |
||
|
f (x) = C; |
|
Р е ш е н и е з а д а ч и с и м п л е к с м е т о д о м |
|
|
|
|
|
|
2x1 + 3x2 |
= C. |
|
|
|
Уравнение линии уровня функции в точке (0, 0): |
|
|
||||
|
|
2x1 + 3x2 |
= 0 . |
|
|
|
На |
чертеже |
линия |
уровня |
функциипрямая |
||
перпендикулярная градиенту. |
|
|
|
|
||
4. Для поиска максимума перемещаем линию уровня |
в |
|||||
направлении градиента до последнего |
касания |
с |
МДР, |
|||
очевидно, |
что касание |
произойдет на |
отрезке |
[В, С], |
||
|
|
193 |
|
|
|
|
Подготовка задачи к решению симплекс-методом
1.Выполнено (ищем максимум).
2.Выполнено (правые части ограничений неотрицательны).
3.Приведем задачу к каноническому виду, для этого введем в
каждое ограничение неотрицательную переменную:
Замечание. Если ограничение имеет знак«<», то вводится переменная со знаком «+», если же ограничение имеет знак «>», то вводится переменная со знаком«-», если исходное ограничение имеет знак «=», то дополнительные переменные не вводятся.
194
2 x1 + 3 x2 + x3 = 1 2
- 2 x1 + 6 x 2 + x 4 = 6
x3 , x4 ³ 0 - д о п о л н и т е л ьн ы е п е р е м е н н ы е
( д о п о л н я ю т н ер а в е н с т в а д о р а в е н св ).
4. Выпишем столбцы коэффициентов при переменных в ограничениях:
|
x1 |
|
x2 |
|
x3 |
|
x4 |
|
æ 2 ö |
æ 3 ö |
æ1 ö |
æ 0 ö |
|||||
ç |
-2 |
÷ |
ç |
÷ |
ç |
÷ |
ç |
÷ |
è |
ø |
è 6 |
ø |
è0 |
ø |
è1 |
ø |
|
ÝÝ
Среди |
столбцов |
имеется |
два |
|
столбца |
единичной матрицы |
||||||||
размерности (2 х 2), они отмечены символом Ý , значит базис есть. |
||||||||||||||
5. Начальное базисное решение: х3, |
х4 - базисные переменные |
|||||||||||||
(переменные |
отмечены |
символом Ý ), эти |
переменные равны |
|||||||||||
правым частям ограничений, в которых они находятся: |
||||||||||||||
х 3 = 12, |
х4 |
= 6. Остальные переменные x1 = x2 = 0. |
||||||||||||
Э т а п в ы ч и с л е н и й |
|
|
|
|
|
|
|
|
|
|||||
Заполним первую таблицу |
|
|
Коэффициенты |
|||||||||||
|
|
функции |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
2 |
3 |
|
0 |
|
0 |
|
C j |
|
|
C i |
|
Б п |
Б р |
x 1 |
x 2 |
|
x 3 |
|
x 4 |
|
ri |
|
|
|
|
0 |
|
x 3 |
12 |
2 |
3 |
|
1 |
|
0 |
|
|
|
|
|
0 |
|
x 4 |
6 |
-2 |
6 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
∆ |
|
|
|
0 |
|
0 |
|
|
|
Коэффициенты |
Правые части |
Столбцы |
|
коэффициентов |
|||
функции при |
ограничений – |
при переменных |
|
базисных |
начальное базисное |
в ограничениях |
|
переменных |
решение |
||
|
|||
|
195 |
|
Базисное решение соответствующее табл. №1:
x1 = 0 x2 = 0 x3 = 12 x4 = 6
Оно соответствует в исходных переменных точке 0(0,0).
Вычислим симплекс-разности для небазисных переменных:
D1 = 2 - |
æ0 |
ö |
æ2 ö |
|
||
ç |
0 |
÷ g |
ç |
÷ |
= 2 - (0 + 0) = 2 |
|
|
è |
ø |
è |
-2 ø |
|
|
|
|
Коэффициенты |
|
|
Столбец |
|
|
Столбец |
||||||
|
|
|
|
|
|
коэффициентов |
||||||||
|
|
функции при |
|
|
коэффициентов |
|
при переменной |
|||||||
|
|
переменной x 1 |
|
|
С i Б |
|
|
|
x 1 |
|||||
D2 |
æ0 ö |
æ3 ö |
|
- (0 |
+ 0) = 3 |
|
|
|
|
|
|
|||
= 3 -ç ÷ |
×ç ÷ = 3 |
|
|
|
|
|
|
|||||||
|
è0 ø |
è6 ø |
|
|
|
|
|
|
|
|
|
|
||
Для базисных переменных симплекс разности равны 0. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
|
|
2 |
|
3 |
0 |
0 |
C j |
|
|
|
C i |
|
Б п |
|
Б р |
|
x 1 |
|
x 2 |
x 3 |
x 4 |
r i |
|
|
|
0 |
|
x 3 |
|
12 |
|
2 |
|
3 |
1 |
0 |
|
|
|
|
0 |
|
x 4 |
|
6 |
|
-2 |
|
6 |
0 |
1 |
|
|
|
|
|
|
|
|
∆ |
|
2 |
|
3 |
0 |
0 |
|
|
Z-столбец
Т.к. ∆2 является максимальной положительной величиной в строке симплекс разностей, то в базис вводится переменная х2. Соответствующий этой переменной столбец - Z-столбец. Вычислим величины r i , как отношения элементов столбца Бр
к элементам Z-столбца:
r = |
12 |
= 4 r = |
6 |
= 1. |
|
|
|||
1 |
3 |
2 |
6 |
|
|
|
|
196
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
2 |
3 |
0 |
0 |
C j |
|
||
C i |
Б п |
Б р |
x 1 |
|
|
x 2 |
x 3 |
x 4 |
r i |
|
0 |
x 3 |
12 |
2 |
|
|
3 |
1 |
0 |
4 |
|
0 |
x 4 |
6 |
-2 |
6 |
0 |
1 |
1 |
Z-строка |
||
|
|
∆ |
2 |
|
|
3 |
0 |
0 |
|
|
Z-столбец
Коэффициент |
Разрешающий |
пересчета |
элемент |
Из базиса выводится |
переменнаях 4 , т.к. ей по строке |
соответствует минимальная неотрицательная величинаr2, соответствующая ей строка - Z-строка.
На пересечении Z-столбца и Z-строки находится разрешающий элемент R = 6.
Осуществим пересчет таблицы:
•запишем коэффициенты функции в верхнюю строку новой таблицы 2;
•запишем в новую таблицу 2 новые базисные переменные
х2 и х3;
• запишем коэффициенты функции при новых базисных
переменных в первый столбец таблицы 2 |
|
Таблица 2 |
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
3 |
0 |
0 |
C j |
|
|
C i |
Б п |
Б р |
x 1 |
x 2 |
x 3 |
x 4 |
ri |
|
|
0 |
x 3 |
|
|
|
|
|
|
|
|
3 |
x 2 |
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
• пересчитаем Z-строку: |
разделим Z-строку на |
|||||||
разрешающий элемент, |
результат запишем в таблицу №2 |
|||||||
на своё место - получится разрешающая строка; |
||||||||
Z-строка |
( |
|
6 |
- 2 |
6 |
0 |
1 ) / 6 |
|
Результат |
|
1 |
-1/ 3 |
1 |
0 |
1/ 6 |
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
|
|
2 |
3 |
|
0 |
0 |
C j |
|
C i |
Б п |
Б р |
x 1 |
x 2 |
|
x 3 |
x 4 |
r i |
|
0 |
x 3 |
|
|
|
|
|
|
|
|
3 |
x 2 |
1 |
-1/3 |
1 |
|
0 |
1/6 |
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
Разрешающая строка |
||||
• пересчитаем оставшуюся строку: умножим разрешающую строку на коэффициент пересчета - 1-й элемент Z-столбца из табл. 1 - это число 3, и вычтем из 1-й строки табл. 1, результат запишем в таблицу №2 на свое место:
Строка 1 табл.1 |
12 |
2 |
3 |
1 |
0 |
|
|
__ |
|
|
|
|
|
Разрешающая строка×(3) |
|
3 |
-1 |
3 |
0 |
1/ 2 |
Результат |
9 |
3 |
0 |
1 |
-1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
|
|
|
|
2 |
3 |
0 |
0 |
C j |
|
|
|
C i |
Б п |
|
Б р |
x 1 |
|
x 2 |
x 3 |
x 4 |
r i |
|
|
0 |
x 3 |
|
9 |
3 |
|
0 |
1 |
-1/2 |
|
|
|
3 |
x 2 |
|
1 |
-1/3 |
1 |
0 |
1/6 |
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
Базисное решение, соответствующее табл. 2: |
|
|
|
||||||||
x1 = 0 |
x2 = 1 |
|
x3 = 9 |
|
|
x4 = 0 |
|
|
|
||
Оно соответствует в исходных переменных точке А = (0,1).
Далее проводим расчет по аналогии.
Вычислим симплекс-разности для небазисных переменных:
198
197
D = |
æ0 |
ö |
æ |
3 |
ö |
= 2 - (0 -1) = 3 |
|
ç |
×ç |
|
÷ |
||||
1 |
|
÷ |
ç -1 |
÷ |
|
||
|
|
è3 |
ø |
è |
3 |
ø |
|
D2 |
|
æ 0 ö |
æ -1 |
ö |
= 2 - (0 +1/ 2) = -1/ 2 |
||
= ç ÷ |
×ç 2 ÷ |
||||||
|
|
è3 |
ø |
ç 1 |
÷ |
|
|
|
|
|
|
è |
6 |
ø |
|
Т.к. ∆1 является максимальной положительной величиной в строке симплекс разностей, то в базис вводится переменная x 1 , соответствующий этой переменной столбец - Z-столбец.
Вычислим величины r i как отношения элементов столбца Б р к элементам Z-столбца:
r = |
9 |
= 3 |
r = |
1 |
= -3 . |
|
|
|
|
||||
1 |
3 |
|
2 |
-1 / 3 |
|
|
|
|
|
|
|
||
Из базиса выводится |
переменнаях 4 , т.к. |
ей по строке |
||||
соответствует минимальная неотрицательная величинаr2 , соответствующая ей строка - Z-строка.
На |
пересечении Z-столбца |
|
|
|
и Z-строки, |
находится |
|||||
разрешающий элемент R = 3. |
|
|
|
|
Таблица 2 |
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
3 |
|
0 |
0 |
C j |
|
||
C i |
Б п |
Б р |
x 1 |
x 2 |
|
x 3 |
|
|
x 4 |
r i |
Z-строка |
0 |
x 3 |
9 |
3 |
0 |
|
1 |
|
|
-1/2 |
3 |
|
3 |
x 2 |
1 |
-1/3 |
1 |
|
0 |
|
|
1/6 |
-3 |
|
|
|
∆ |
3 |
0 |
|
0 |
-1/2 |
|
|
||
Z-столбец
Осуществим пересчет таблицы:
•запишем коэффициенты функции в верхнюю строку новой табл. 3;
•запишем в новую табл. 3 новые базисные переменные x2 и x1;
•запишем коэффициенты функции при новых базисных переменных в первый столбец табл. 3;
|
|
|
|
|
|
|
Таблица 3 |
|
|
|
|
2 |
3 |
0 |
0 |
C j |
|
C i |
Б п |
Б р |
x 1 |
x 2 |
x 3 |
x 4 |
r i |
|
0 |
x 1 |
|
|
|
|
|
|
|
3 |
x 2 |
|
|
|
|
|
|
|
∆
• пересчитаем Z-строку: разделим Z-строку на разрешающий элемент, результат запишем в табл. 3 на своё место – получится разрешающая строка;
Z-строка ( |
9 |
3 |
0 |
1 |
-1/ 2 |
) / 3 |
|
||||||
Результат |
3 |
1 |
0 |
1/ 3 |
-1/ 6 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
|
|
|
|
|
2 |
3 |
|
0 |
|
0 |
|
C j |
|
|
C i |
Б п |
|
Б р |
x 1 |
|
x 2 |
|
x 3 |
|
x 4 |
|
r i |
|
0 |
x 1 |
|
3 |
1 |
|
0 |
|
1/3 |
|
-1/6 |
|
|
|
3 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разрешающая строка |
||||||
• пересчитаем оставшуюся строку: умножим разрешающую строку на коэффициент пересчета – 2-й элемент Z-столбца из табл. 2 – это число (-1/3) и вычтем из 2-й строки табл. 2 результат запишем в табл. 3 на своё место:
Строка 2 табл.2 |
1 |
-1/ 3 |
1 |
0 |
|
1/ 6 |
__ |
|
|
|
|
|
|
Разрешающая строка×(-1/3) |
3 |
1 |
0 |
1/ 3 |
-1/ 6 |
|
Результат |
2 |
0 |
1 |
1/ |
9 |
1/ 9 |
200
199
