
2780
.pdf
Решение. Составим рабочую таблицу Гаусса (табл. 4.4). При поиске начального базисного допустимого решения в качестве разрешающего имеет смысл брать столбец с отрицательным коэффициентом индексной строки, так как при решении задачи на минимум (min обозначен в индексной строке первого блока, но в целях экономии места в дальнейших блоках это будем опускать) положительные коэффициенты нужно сохранять (см. теорему оптимальности). При выборе разрешающей строки следует соблюдать рекомендации п.4.3 (минимальное значение θ подчеркнуто).
Каждая итерация выполнена по правилу прямоугольника, вычисления — по формулам Жордана-Гаусса. Первое допустимое базисное решение оказалось оптимальным.
Ответ: Х1 = (15/8,9/4,0,0,0,9), Lmin = L(Х1) = 135/8.
Пример 4.3.
L(X ) = 2x1 − x2 +3x3 −2x4 −10x5 → max,
x1 − x2 +2x3 −2x4 −6x5 ≤ 20,x1 +2x2 − x3 +7x4 +3x5 ≤ 50,−x1 + x2 + x3 + x4 ≤ 40,
xj ≥ 0, j =1,5.
41
|
|
|
|
|
|
|
|
Таблица 4.4 |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
св.чл. |
θ |
|
|
6 |
11 |
8 |
-1 |
-1 |
0 |
36 |
|
|
|
4 |
2 |
7 |
0 |
-1 |
1 |
21 |
21:1 |
|
|
8 |
8 |
12 |
-1 |
-1 |
1 |
42,min |
42:1 |
|
|
-7 |
-8 |
-11 |
1 |
2 |
-1 |
-57 |
36:11 |
|
|
6 |
11 |
8 |
-1 |
-1 |
0 |
36 |
|
|
|
4 |
2 |
7 |
0 |
-1 |
1 |
21 |
21:2 |
|
|
4 |
6 |
5 |
-1 |
0 |
0 |
21 |
21:6 |
|
|
-3 |
-6 |
-4 |
1 |
1 |
0 |
-36 |
36/11:6/11 |
|
|
6/11 |
1 |
8/11 |
-1/11 |
-1/11 |
0 |
36/11 |
|
|
|
32/11 |
0 |
61/11 |
2/11 |
-9/11 |
1 |
159/11 |
159/11:32/11 |
|
|
8/11 |
0 |
7/11 |
-5/11 |
6/11 |
0 |
15/11 |
15/11:8/11 |
|
|
3/11 |
0 |
4/11 |
5/11 |
5/11 |
0 |
-180/11 |
|
|
|
0 |
1 |
1/4 |
3 |
-1/2 |
0 |
9/4 |
|
|
|
0 |
0 |
3 |
2 |
3 |
1 |
9 |
|
|
|
1 |
0 |
7/8 |
-5/8 |
3/4 |
0 |
15/8 |
|
|
|
0 |
0 |
1/8 |
5/8 |
1/4 |
0 |
-135/8 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Применить непосредственно симплексный метод к этой задаче нельзя, ее форма не каноническая. Введем три дополнительных переменных x6, x7, x8 и запишем задачу в канонической форме:
L(X ) = 2x1 − x2 +3x3 −2x4 −10x5 +0x6 +0x7 +0x8 → max,
x1 − x2 +2x3 −2x4 −6x5 + x6 = 20,x1 +2x2 − x3 +7x4 +3x5 + x7 = 50,−x1 + x2 + x3 + x4 + x8 = 40,
xj ≥ 0, j =1,8.
Заметим, что система ограничений приведена к
42

единичному базису, а значит, решение Х1 = (0, 0, 0, 0, 0, 20, 50, 40) –
базисное допустимое. Оно неоптимальное, потому что среди коэффициентов L(Х) при свободных переменных есть положительные (см. теорему оптимальности). Составим таблицу Гаусса (табл. 4.5) и найдем базисные решения, для которых коэффициенты L(Х) будут неположительными (в тривиальных ситуациях столбец θ не обозначен):
В каждом блоке таблицы имеем базисные допустимые решения. Одно из них, Х1, отмечено выше. Далее, Х2 = (20,0,0,0,0,0,30,60).
Таблица 4.5
x1 x2 x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
св.чл. |
||
1 |
-1 2 |
-2 |
-6 |
1 |
0 |
0 |
20 |
|
1 |
2 |
-1 |
7 |
3 |
0 |
1 |
0 |
50 |
-1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
40 |
2 |
-1 |
3 |
2 |
-10 |
0 |
0 |
0 |
Max |
1 |
-1 2 |
-2 |
-6 |
1 |
0 |
0 |
20 |
|
0 |
3 |
-3 |
9 |
9 |
-1 |
1 |
0 |
30 |
0 |
0 |
3 |
-1 |
-6 |
1 |
0 |
1 |
60 |
0 |
1 |
-1 |
2 |
2 |
-2 |
0 |
0 |
-40 |
1 |
0 |
1 |
1 |
3 |
2/3 |
1/3 |
0 |
30 |
0 |
1 |
-1 |
3 |
3 |
-1/3 |
1/3 |
0 |
10 |
0 |
0 |
3 |
-1 |
-6 |
1 |
0 |
1 |
60 |
0 |
0 |
0 |
-1 |
-1 |
-3 |
-1 |
0 |
-50 |
1 |
0 |
0 |
4/3 |
5 |
1/3 |
1/3 |
0 |
10 |
0 |
1 |
0 |
8/3 |
1 |
0 |
1/3 |
1/3 |
30 |
0 |
0 |
1 |
-1/3 |
-2 |
1/3 |
0 |
1/3 |
20 |
0 |
0 |
0 |
-1 |
-1 |
-3 |
-1 |
0 |
-50 |
неоптимальное. В третьем блоке имеем первое оптимальное решение X3 = (30,10,0,0,0,0,0,60) с L(X3) = 50. Заметим, что
один из коэффициентов при свободной переменной x3 можно
43
ввести в базис, не изменяя при этом значение L(X). Это приводит к другому оптимальному решению:
X4 = (10,30,20,0,0,0,0,0) с L(X3) = 50.
Таким образом, задача имеет бесконечное множество решений. Прежде чем записать их, отбросим дополнительные переменные x6, x7, x8. Получаем вырожденное оптимальное решение X3 = (30,10,0,0,0,) и невырожденное решение X4 = (10,30,20,0,0), а из них - общее решение
X = t • Х3 + (1 - t) • Х4, 0 < t < 1, Lmax = 50.
Ответ: X = t • Х3 + (1 - t) • Х4, 0 < t < 1, Lmax = 50,
X3 = (30,10,0,0,0), |
X4 = (10,30,20,0,0). |
Примечание. Заметим, |
что каждый раз разрешающий |
коэффициент мы брали, исходя из простоты последующих вычислений. Однако нежелательно, чтобы простота вычислений приводила к дополнительным положительным коэффициентам индексной строки. Именно этого мы старались избегать.
Пример 4.4.
L(X ) = x1 − x2 − x3 +3x4 −2x5 → extr,
x1 + x2 −3x4 +4x5 =11,x2 + x3 +3x4 +6x5 = 33,
−2x1 −2x2 + x3 +10x4 −5x5 = 2, xj ≥ 0, j =1,5.
Решение. Эта задача задана в канонической форме. Она может быть решена симплексным методом. Имеем n – m = 2, ранг системы уравнений равен r = m = 3, поэтому ее также можно решить графически. В единой таблице Гаусса (табл. 4.6) выполним все нужные нам операции по разрешению системы условий относительно трех базисных неизвестных,
44

скажем, х1, х2, х3, и выражение линейной формы через свободные неизвестные x4, х5. В четвертом блоке получим решение задачи на минимум, в пятом — на максимум. Систему условий, полученную в четвертом блоке, используем для графического решения.
Из четвертого блока таблицы выписываем допустимое базисное оптимальное решение на минимум:
Xmin = (2,9,24,0,0), Lmin(X) = -31.
Из пятого блока выписываем допустимое базисное оптимальное решение на максимум:
Xmax = (14,15,0,6,0),
Lmax(X) = 17.
Из четвертого блока получаем решение системы условий относительно х1, х2, х3, а линейную функцию L(Х) выражаем через свободные переменные x4 и х5:
x |
= 2 +2x |
− x |
, |
|
|
1 |
4 |
|
5 |
|
|
x2 |
= 9 + x4 −3x5 |
, |
(*) |
||
x |
= 24 −4x |
|
−3x , |
||
4 |
|
||||
3 |
|
|
5 |
|
|
Используя неотрицательность базисных переменных, задачу можно сформулировать геометрически:
найти экстремум линейной целевой функции
L(X) = -31 + 8x4 + 3x5 → extr,
при ограничениях:
2x4 − x5 ≥ −2,x4 −3x5 ≥ −9,
4x4 +3x5 ≤ 24.
45
Таблица 4.6
|
x1 x2 |
x3 |
x4 |
x5 |
св.чл. |
|
|
1 |
1 |
0 |
-3 |
4 |
11 |
|
|
0 |
1 |
1 |
3 |
6 |
33 |
|
|
-2 |
-2 |
1 |
10 |
-5 |
2 |
|
|
|
1 |
-1 |
-1 |
3 |
-2 |
1 |
|
|
1 |
1 |
0 |
-3 |
4 |
11 |
|
0 |
1 |
1 |
3 |
6 |
33 |
|
|
0 |
0 |
1 |
4 |
3 |
24 |
|
|
|
0 |
-2 |
-1 |
6 |
-6 |
-11 |
|
|
1 |
0 |
-1 |
-6 |
-2 |
-22 |
|
0 |
1 |
1 |
3 |
6 |
33 |
|
|
0 |
0 |
1 |
4 |
3 |
24 |
|
|
|
0 |
0 |
1 |
12 |
6 |
55 |
|
|
1 |
0 |
0 |
-2 |
1 |
2 |
|
0 |
1 |
0 |
-1 |
3 |
9 |
|
|
0 |
0 |
1 |
4 |
3 |
24 |
|
|
|
0 |
0 |
0 |
8 |
3 |
31 |
|
|
1 |
0 |
0 |
0 |
5/2 |
14 |
|
0 |
1 |
0 |
0 |
15/4 |
15 |
|
|
0 |
0 |
1/4 |
1 |
3/4 |
6 |
|
|
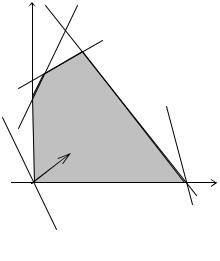
Из рис. 4.1 |
0 |
0 |
-1 |
0 |
-3 |
-17 |
|
видно, что целевая функция двух переменных |
|||||||
x4 и х5 |
|
L(X) = -31 + 8x4 + 3х5 |
|||||
|
|
|
|||||
достигает максимального |
значения |
в точке A(6,0) и |
|||||
минимального значения в начале координат 0(0,0). Значения остальных неизвестных находим из системы (*). При х4 = 6, х5 = 0 находим
х1 |
= 14, |
х2 = 15, |
х3 =0, |
а при х4 = 0, х5 = 0 находим |
|||
х1 |
=2, |
х2 = 9, |
х3 = 24. |
46
x5
|
|
|
B |
|
3 |
C |
|
|
|
|
|
|
|
|
2 D |
|
|
q |
|
|
|
|
|
G |
|
|
|
|
|
|
|
n |
|
6 |
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
A x4 |
p
Рис. 4.1
Таким образом, базисному допустимому решению, полученному симплексным методом, соответствует вершина многоугольника G представляющего геометрическое изображение ОДР.
Пример 4.5.
L(X ) = 2x1 +3x2 − x3 → max,
x1 − x2 + x3 = 5,2x2 + x3 ≤12,2x1 −3x2 − x3 ≥ 4,
x1 ≥ 0, x2 ≥ 0.
Решение. Условия задачи имеют смешанный характер, они состоят из равенства и неравенств разных направлений. Кроме того, заметим, что на переменную х3 не накладывается условие неотрицательности. Решение задачи возможно несколькими
способами. |
|
|
Способ 1. Приведем |
задачу к |
каноническому виду |
и решим ее симплексным |
методом. |
Для этого положим |
х3 = х4 – х5, где х4 > 0, х5 > 0. Тем самым, все переменные
47
задачи стали неотрицательными. Остается перейти к условиям-равенствам:
L(X ) = 2x1 +3x2 − x4 + x5 → max,
x1 − x2 + x4 − x5 = 5,2x2 + x4 − x5 + x6 =12,
2x1 −3x2 − x4 + x5 − x7 = 4, x1 ≥ 0, x2 ≥ 0, x4 ≥ 0,
x5 ≥ 0, x6 ≥ 0, x7 ≥ 0.
Построим таблицу Гаусса (табл. 4.7).
Рассматривая второй блок таблицы, видим, что в базис можно ввести только х1 . Разрешающий коэффициент а11 = 3 приводит к недопустимому решению Х1 = (3,0,0,-2,10,0). Из четвертого блока получаем базисное допустимое вырожденное неоптимальное решение Х2 = (11,6,0,0,0,0).
Сначала отметим эффект второй итерации. Разрешающий коэффициент а1 1 = 3 должен привести к недопустимому решению, так как не соблюдено правило выбора разрешающей строки. В самом деле свободный коэффициент третьего уравнения отрицателен, но при этом переменные х2, х3, x7 — допустимые.
Решение Х2 = (11,6,0,0,0,0) — вырожденное, базисное, допустимое решение; оно неоптимальное, так как в индексной строке имеем один положительный коэффициент при х7. В базис нужно ввести только эту переменную х7. Но коэффициенты этого столбца отрицательны, а это приведет к недопустимому решению. Поэтому дальнейшие итерации прекращаются с выводом: задача не имеет решения по причине неограниченности целевой функции, т. е. max L(Х) = + ∞. Значит, к первоначальным переменным х1, х2, х3 можем не
возвращаться.
48
|
|
|
|
|
|
|
|
Таблица 4.7 |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x4 x5 |
x6 |
x7 |
св.чл. |
θ |
||
|
1 |
-1 |
1 |
-1 |
0 |
0 |
5 |
|
|
|
0 |
2 |
1 |
-1 |
1 |
0 |
12 |
|
|
|
2 |
-3 |
-1 |
1 |
0 |
-1 |
4 |
|
|
|
2 |
3 |
-1 |
1 |
0 |
0 |
max |
9:3 |
|
|
3 |
-4 |
0 |
0 |
0 |
-1 |
9 |
|
|
|
2 |
-1 |
0 |
0 |
1 |
-1 |
16 |
16:2 |
|
|
2 |
-3 |
-1 |
1 |
0 |
-1 |
4 |
4:2 |
|
|
0 |
6 |
0 |
0 |
0 |
1 |
-4 |
|
|
|
1 |
-4/3 |
0 |
0 |
0 |
-1/3 |
3 |
|
|
|
0 |
0 |
0 |
0 |
1 |
-1/3 |
10 |
|
|
|
|
5/3 |
|
|
|
|
|
|
|
|
0 |
-1/3 |
-1 |
1 |
0 |
-1/3 |
-2 |
|
|
|
0 |
6 |
0 |
0 |
0 |
1 |
-4 |
|
|
|
1 |
0 |
0 |
0 |
0 |
-3/5 |
11 |
|
|
|
0 |
1 |
0 |
0 |
3/5 |
-1/5 |
6 |
|
|
|
0 |
0 |
-1 |
1 |
0 |
-2/5 |
0 |
|
|
|
0 |
0 |
0 |
0 |
-18/5 |
11/5 |
-40 |
|
|
|
|
|
|
|
|
|
|
|
|
Способ 2, геометрический, предлагаем реализовать самостоятельно, используя следующие рекомендации. Рассмотрим систему ограничений
x1 − x2 + x3 = 5,2x2 + x3 + x6 =12,
2x1 −3x2 − x3 − x7 = 4, x1 ≥ 0, x2 ≥ 0, x6 ≥ 0, x7 ≥ 0,
Здесь замена х3 = х4 - х5 не произведена, т.е. х3 - произвольного знака. Из первого уравнения исключаем х3:
х3 = 5 - x1 + х2, 49
и это выражение подставляем в линейную функцию:
L(Х) = Зх1 + 2х2 - 5.
Оставшаяся система из двух уравнений может быть представлена (с учетом равенства х3 = 5 – х1 + х2) в виде
x |
= 7 |
+ x |
−3x |
, |
x |
−3x |
|
≥ −7, |
6 |
|
1 |
2 |
|
1 |
|
2 |
|
x7 |
= −9 +3x1 −4x2 |
3x1 −4x2 |
||||||
x1 ≥ 0, x2 ≥ 0
(система неравенств получена из условий х6 > 0 и х7 > 0), и задача может быть решена графически.
Обратим внимание на то, что по ходу решения задачи на максимум
max L(X) = + ∞
в таблице Гаусса легко обнаружить решение задачи на минимум
Lmin = L(3,0) = 4, x1 = 3, x2 = 0, x3 = 2
Это решение было найдено в третьем блоке табл. 4.7.
Ответ: max L(Х) = + ∞.
Пример 4.6. Для изготовления четырех видов продукции Р1, Р2, Р3 и Р4 используются три вида сырья S1, S2, S3. Запасы сырья, нормы расхода сырья на единицу продукции и получаемая прибыль от реализации единицы продукции заданы в таблице 4.8.
|
|
|
|
|
Таблица 4.8 |
|
Вид сырья |
Нормы расхода |
Запасы |
|
|||
|
P1 |
P2 |
P3 |
P4 |
сырья |
|
S1 |
4 |
2 |
1 |
8 |
1200 |
|
S2 |
2 |
10 |
6 |
0 |
600 |
|
S3 |
3 |
0 |
6 |
1 |
1500 |
|
Прибыль (ден. ед.) |
15 |
6 |
12 |
24 |
max |
|
|
|
50 |
|
|
|
|

Определить оптимальный план выпуска продукции, при котором прибыль от ее реализации будет максимальной.
Решение. Обозначим через X = (х1, х2, х3, х4) план выпуска продукции (хj > 0 - количество единиц продукции вида j,
которое предполагается производить). Требуется найти тот план X = (х10, х20, х30, х40) при котором прибыль будет
максимальной, т.е. тот набор неотрицательных чисел, который доставляет наибольшее значение целевой функции:
L(X) = 15х1 + 6х2 + 12х3 + 24х4 → max,
при следующих ограничениях, связанных с имеющимися запасами сырья:
4x1 +2x2 + x3 +8x4 ≤1200,2x1 +10x2 +6x3 ≤ 600,3x1 +6x3 + x4 ≤1500,
xj ≥ 0, j =1, 4.
Решение. Приводим задачу к каноническому виду:
L(X ) =15x1 +6x2 +12x3 + 24x4 +0x5 +0x6 +0x7 → max,
4x1 +2x2 + x3 +8x4 + x5 =1200,2x1 +10x2 +6x3 + x6 = 600,3x1 +6x3 + x4 + x7 =1500,
xj ≥ 0, j =1,7.
Заносим данные задачи в таблицу Гаусса (табл. 4.9), выполним необходимые симплексные преобразования, приводящие к оптимальному решению.
51
|
|
|
|
|
|
|
Таблица 4.9 |
||
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 св.чл. |
|||
4 |
2 |
1 |
8 |
1 |
0 |
0 |
1200 |
|
|
2 |
10 |
6 |
0 |
0 |
1 |
0 |
600 |
|
|
3 |
0 |
6 |
0 |
0 |
0 |
1 |
1500 |
|
|
15 |
6 |
12 |
24 |
0 |
0 |
0 |
max |
|
|
1/2 |
1/4 |
1/8 |
0 |
1/8 |
0 |
0 |
150 |
|
|
2 |
10 |
6 |
0 |
0 |
1 |
0 |
600 |
|
|
3 |
0 |
6 |
0 |
0 |
0 |
1 |
1500 |
|
|
3 |
0 |
9 |
2 |
-3 |
0 |
0 |
-3600 |
|
|
11/24 |
1/24 |
0 |
1 |
1/8 |
-1/48 |
0 |
275/2 |
|
|
1/3 |
5/3 |
1 |
0 |
0 |
1/6 |
0 |
100 |
|
|
1 |
-10 |
0 |
0 |
0 |
-1 |
-1 |
1400 |
|
|
0 |
-15 |
0 |
0 |
-3 |
-3/2 |
0 |
-4500 |
|
|
Полученное решение X = (0,0,100,275/2,0,0,1400) —
оптимальное (индексная строка не содержит положительных коэффициентов). Оставляем первые четыре компонента (в задаче имеем только четыре вида продукции). Получаем X = (0,0,100,275/2). При этом прибыль равна
L(0,0,100,275/2) = 4500 (ден. ед.).
Посмотрим, как этот план сказывается на использовании сырья. План предусматривает производство 100 единиц продукции Р3 и 275/2 единиц продукции Р4; продукции Р1 и Р2 производить не нужно. При этом сырье S1 использовано полностью (100 + 8 · 275/2 = 1200 ед.), сырье S2 использовано полностью (6 · 100 + 1 · 275/2 = 737,5 ед.; 762,5 ед. сырья S3
остается неиспользованным).
Ответ: X = (0,0,100,275/2), L(0,0,100,275/2) = 4500 ден. ед.
52
Вопросы для самопроверки
4.1.Какую роль играет в симплексном методе разрешающий (ведущий) коэффициент?
4.2.Чем отличается вырожденное решение от невырожденного?
4.3.При каких условиях допустимое базисное решение является оптимальным?
4.4.Может ли оптимальное решение быть вырожденным?
4.5В чем состоит симплексный метод решения задач ЛП?
4.6Каким образом следует выбирать разрешающий
столбец при переходе от одного к другому базису?
4.7.Каким образом следует выбирать разрешающую
строку?
4.8.Какие последствия влечет отрицательность коэффициентов системы ограничивающего столбца?
4.9.Может ли симплексный метод приводить к бесконечному множеству решений?
4.10.Какой вывод можно сделать из того, что задача не имеет допустимого базисного решения?
4.11.Можно ли симплексным методом решить заданную симметрически задачу линейного программирования?
4.12.Можно ли симплексным методом решить задачу линейного программирования, если на некоторые ее переменные не наложены условия неотрицательности?
5. Двойственность в линейном программировании
5.1. Предположим, что задача линейного программирования задана в следующем виде:
53
L(X ) = c1 x1 +c2 x2 +... |
|
+cn xn → max(или min), |
|||||||||||
|
a x +a x |
+ |
+a |
|
x |
n |
≤ b ,(или≥ b ) |
|
y |
||||
|
|
||||||||||||
|
11 1 |
11 1 |
|
|
1n |
|
1 |
1 |
|
|
1 |
||
a21 x1 +a21 x1 +... |
+a2n xn |
≤ b2 ,(или ≥ b2 ) |
|
y2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
... (5.10) |
|
|
.......................................................... |
|
|
|
|
|
|
|
|
|
|
||
a |
x +a |
x |
+... |
+ a |
|
|
x |
≤ b ,(или≥ b ) |
|
y |
m |
||
|
m1 1 |
m1 1 |
|
|
mn n |
m |
m |
|
|
||||
x1 ≥ 0, x2 ≥ 0,..., xn ≥ 0.
Составим другую задачу линейного программирования, число переменных которой равно числу ограничений данной задачи, т.е. m. Обозначим их буквами у1, у2, ..., уm (они записаны справа от системы ограничений приведенной задачи). Эта задача имеет вид:
F (Y ) = b1 y1 +b2 y2 +... |
+bm ym → min(или max) |
|||||||||||||||
a |
y |
+a |
|
y |
2 |
+... |
+a |
m1 |
y |
m |
≥ c ,(или ≤ c ) |
|
||||
11 |
1 |
21 |
|
|
|
|
|
|
1 |
1 |
|
|||||
a12 y1 +a22 y2 +... |
+am2 ym ≥ c2 ,(или ≤ c2 ) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.11) |
.......................................................... |
||||||||||||||||
a y +a |
y |
2 |
+... |
+a |
|
y |
m |
≥ c |
,(или ≤ c |
) |
||||||
1n 1 |
2n |
|
|
|
mn |
|
|
m |
m |
|
||||||
|
|
y1 ≥ 0, y2 |
≥ 0,..., ym ≥ 0. |
|
||||||||||||
Вторая задача называется двойственной, или сопряженной для первой, а первая — прямой, или основной.
Если для второй задачи составить двойственную задачу, то получим первую. Таким образом, сформулированные задачи составляют пару взаимно двойственных, или взаимно сопряженных задач линейного программирования.
Отметим особенности пары взаимно двойственных задач. 1) Если основная задача — задача на максимум (минимум), то система ограничений должна состоять из
54
неравенств вида < (>), и в таком случае двойственная задача должна быть задачей на минимум (максимум), а ее система ограничений должна состоять из неравенств вида > (<).
2)В основной задаче все переменные должны быть неотрицательными.
3)Коэффициентами целевой функции F(У) двойственной задачи являются свободные члены системы ограничений основной задачи, и их число равно m.
4)Основная матрица системы ограничений двойственной задачи получается транспонированием матрицы системы ограничений основной задачи.
5)Свободными членами системы ограничений двойственной задачи являются коэффициенты целевой функции основной задачи.
6)Все переменные двойственной задачи неотрицательные.
5.2. Предположим теперь, что основная задача задана в ослабленной форме, т.е. среди ее переменных имеются переменные произвольного знака (на них не наложено требование неотрицательности), а система ограничений содержит неравенства противоположных направлений и, возможно, равенства. Построение двойственной задачи в таком случае основано на следующих правилах.
1)Все неравенства системы ограничений основной задачи следует привести к одному направлению: > в задаче на минимум или < в задаче на максимум.
2)Если в системе ограничений основной задачи имеется
равенство (уравнение), то та переменная уi , которая соответствует этому i-му ограничению-равенству, может быть произвольного знака. Запишем это соответствие так:
ai 1 x1 + ai 2 x2 + … + ai n xn = bi → yi R
3) Если на некоторую переменную xi основной задачи не
55
наложено условие неотрицательности, то соответствующее ей ограничение двойственной задачи является равенством:
xi R → a1 j y1 + a2 j y2 + … + amj ym = ci .
5.3. Для основной задачи линейного программирования и двойственной к ней задачи справедливы следующие теоремы.
Теорема 5.1. Если одна из пары двойственных задач линейного программирования имеет решение, то и другая задача имеет решение, и при этом значения целевых функций
этих задач равны: L(Xопт) = F(Yопт).
Теорема 5.2. Произвольное допустимое базисное решение одной задачи из пары двойственных оптимально тогда и только тогда, когда система ограничений двойственной задачи совместна.
Теорема 5.3. Если целевая функция одной из пары двойственных задач неограничена снизу (сверху), то система ограничений другой задачи этой пары несовместна.
5.4. Если основная задача линейного программирования допускает экономическую интерпретацию, то аналогичную интерпретацию можно придать и двойственной задаче. Обратимся к одной из множества таких возможностей. Предположим, что основная задача представляет собой задачу наилучшего использования сырья (см. пример 2.2). Математическая модель этой задачи описывается условиями (5.10) (задача на максимум с системой неравенств направления <).
Двойственная задача
Предположим, что имеется второй производитель, который хочет перекупить сырье, а следовательно, ему нужно минимизировать суммарные затраты на приобретение всех видов сырья. Введем величины оценок (цен) всех видов сырья S1, S2, ..., Sm, которые обозначим через у1, у2,…, уm (уi — стоимость единицы сырья Si, bi yi — стоимость запаса bi этого
56
сырья). Стоимость всего сырья равна
F (Y ) = b1 y1 +b2 y2 +... +bm ym → min ,
и она подлежит минимизации.
Первому производителю невыгодно продавать сырье, если суммарная стоимость всех видов сырья, расходуемых на каждый вид продукции, меньше прибыли c i , получаемой при реализации этого вида продукции. Таким образом, приходим к системе ограничений, совпадающей с системой (5.11):
a11 y1 +a21 y2 +... +am1 ym ≥ c1 ,
...........................................
a1n y1 +a2n y2 +... +amn ym ≥ cn ,
Условия yi > 0, i = 1,2,…,m, вполне естественны.
Этим установлена связь между двумя взаимно двойственными задачами линейного программирования.
Для следующих задач линейного программирования построим соответствующие им двойственные задачи.
Пример 5.1.
L(X ) = 2x1 +3x2 − x3 |
→ min, |
||||||
|
x |
+ |
2x |
− x ≥ 3, |
|
|
y |
|
|||||||
|
1 |
|
2 |
3 |
|
|
1 |
2x1 − x2 +2x3 ≥ −1, |
|
y2 |
|||||
|
|
x |
+3x ≥ 2, |
|
|
y |
|
|
|
1 |
|
3 |
|
|
3 |
|
|
|
|
||||
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0.
Решение. Прямая задача удовлетворяет условиям п. 5.1. а) В прямой задаче имеем три ограничения. В
двойственной задаче имеем три переменные у1 , у2 , у3 (они уже записаны в условиях прямой задачи).
57
б) Целевая функция строится по свободным членам системы ограничений прямой задачи, а сопряженная задача — задача на максимум:
F(Y) = 3y1 – y2 +2y3 → max.
в) Поскольку переменные прямой задачи неотрицательны, система ограничений двойственной задачи состоит только из неравенств, противоположных неравенствам прямой задачи, а коэффициенты систем ограничений двойственной и прямой задач составляют транспонированные матрицы:
y1 +2y2 + y3 ≤ 2,2 y1 − y2 ≤ 3,
−y1 +2y2 +3y3 ≤ −1.
г) Так как система ограничений прямой задачи состоит только из неравенств, то переменные двойственной задачи неотрицательны:
y1 > 0, y2 > 0, y3 > 0,
Ответ:
F (Y ) = 3y1 − y2 +2y3 → max,
y1 +2y2 + y3 ≤ 2,2 y1 − y2 ≤ 3,
−y1 +2y2 +3y3 ≤ −1. y1 ≥ 0, y2 ≥ 0, y3 ≥ 0,
58
Пример 5.2.
L(X ) =1+ x1 −2x2 +3x3 −5x4 → min,
x1 +2x2 − x3 +2x4 = 5,−2x1 − x2 +5x3 − x4 ≤ −2,3x1 + x2 −2x3 ≤ −5,
x1 ≥ 0, x3 ≥ 0.
Решение. Задача не отвечает требованиям п. 5.1. Будем действовать согласно рекомендациям п. 5.2. Сначала преобразуем систему ограничений: равенство сохраним, а неравенства приводим к виду >. Имеем
x |
+2x |
− x +2x |
4 |
= 5, |
|
y |
||
|
||||||||
|
1 |
2 |
|
3 |
|
|
1 |
|
2x1 + x2 −5x3 + x4 ≥ 2, |
|
y2 |
||||||
|
−3x − x |
+2x |
≥ 5. |
|
y |
|||
|
|
1 |
2 |
3 |
|
|
|
3 |
Сопряженная задача содержит три переменные у1 , у2 , у3 , причем у1 может быть произвольного знака (первое условие в системе ограничений есть равенство). Второе и четвертое условия в системе ограничений двойственной задачи будут равенствами (на х2 и x4 не распространяется условие неотрицательности). Получаем (свободный член L(X) становится свободным членом F(Y)):
F (Y ) =1+5y1 +2y2 +5y3 → max,
y1 +2y2 −3y3 ≤1,2 y1 + y2 − y3 = −2,−y1 −5y2 +2 y3 ≤ 3,
2 y1 + y2 = −5, y2 ≥ 0, y3 ≥ 0.
Пример 5.3. |
Дана |
основная |
задача |
линейного |
|
программирования |
L(X ) = 2x1 +3x2 |
→ max, |
|
||
|
|
||||
|
x −3x |
|
≤ 6, |
|
|
|
1 |
2 |
|
|
|
|
−2x1 + x2 ≤ 4, |
|
|
||
xj ≥ 0, j =1, 2.
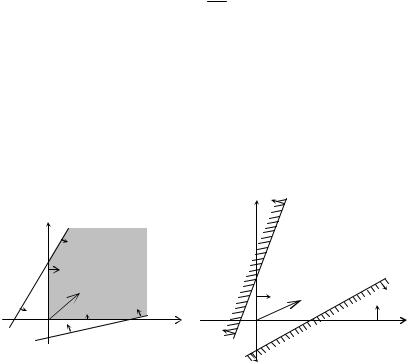
Составить двойственную задачу и решить обе эти задачи. Решение. Основную задачу можно решить графически.
Исходя из построенного чертежа (рис. 5.1), заключаем, что задача не имеет решения по причине неограниченности целевой функции в направлении n в области допустимых решений задачи. Таким образом,
|
|
max L(X ) = +∞ |
|
|
|
x G |
|
|
|
y2 |
2) |
|
|
|
|
x2 |
|
|
|
4 |
G |
|
G= |
2) |
|
3 |
1) |
|
n |
|
nx1 |
-2 O |
6 |
-1 |
2 |
-2 |
1) |
x1 |
y1 |
|
|
|
|
|
|
-2 |
|
|
Рис. 5.1 |
|
Рис. 5.2 |
Составим теперь двойственную задачу. Она имеет вид
60
59
