
2450
.pdf
Решение уравнения (1.54) должно также удовлетворять постулату Жуковского - Чаплыгина о конечности поля скоростей во всей области течения, включая заднюю кромку крыла.
Для колеблющегося крыла решение уравнения (1.54) может быть получено по методу Теодорсена [4, 20], в соответствии с которым крыло заменяется системой источников и стоков и совокупностью вихрей, а спутная струя заменяется совокупностью вихрей той же интенсивности, что и крыло, но противоположного направления. Каждый из потоков находится путем применения конформного преобразования Н.Е. Жуковского для отображения окружности на контур профиля.
В результате получается, что скорость q , создаваемая в
произвольной точке окружности всем слоем источников и стоков, удовлетворяющих граничному условию (1.55), может быть определена из следующего соотношения [4]:
|
2 |
|
Vy |
п |
, t sin 2 |
|
q , t |
|
|
|
|
d . (1.56) |
|
|
|
|
|
|
||
|
0 |
cos |
cos |
|||
Этой скорости соответствует следующий потенциал возмущения скорости на верхней половине окружности [4]:
|
|
B VУ |
п |
sin |
|
|||
|
, t |
|
|
|
|
d d . |
(1.57) |
|
B |
|
|
|
|
|
|||
|
|
0 cos |
|
cos |
|
|||
|
|
|
|
|
||||
Подстановка (1.57) в уравнение (1.50) с учетом антисимметричности течения, создаваемого источниками и стоками, приводит к следующему выражению для разности давлений на верхней и нижней поверхности профиля:
21
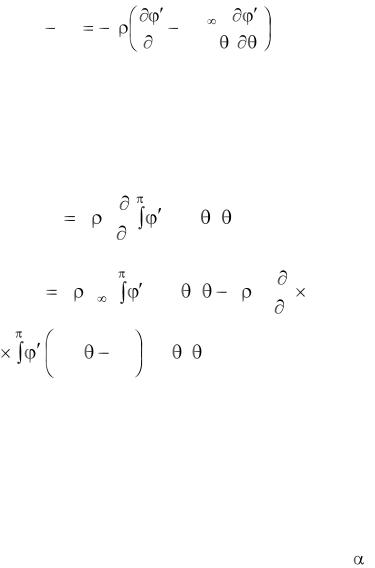
Pв Pн |
2 |
|
|
V |
|
в |
. (1.58) |
|
|
|
|
||||
t вsin |
|
|
|
||||
|
|
|
|
|
|||
Интегрирование (1.58) по поверхности крыла единичного размаха приводит к следующим выражениям для подъемной силы и продольного момента профиля относительно точки x r , обусловленным бесциркуляционным
потоком, создаваемым источниками и стоками:
Y |
|
2 |
в |
|
|
|
вsin |
d . |
|
(1.59) |
||
|
|
|
||||||||||
б.ц |
|
|
|
t 0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Mб.ц |
|
2 V в |
вsin |
d |
2 в2 |
|
|
|||||
|
t |
. (1.60) |
||||||||||
|
|
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
cos |
|
x1 |
|
sin |
d |
|
|
|
|||
в |
|
|
в |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|||
Равенства (1.59) и (1.60) справедливы для любого неустановившегося течения.
Из (1.59) следует, что в случае установившегося движения подъемная сила, обусловленная бесциркуляционным характером течения, равна нулю.
Для динамики летательных аппаратов практический интерес представляет случай, когда крыло совершает вертикальные перемещения h(t) и поворачивается относительно оси, проходящей через точку Х т , на угол (t) .
В этом случае функция yn (x, t) , характеризующая
мгновенное значение малого смещения линии хорды, имеет вид:
22

Уn |
x, t |
|
|
h |
|
x |
xT . |
|
|
(1.61) |
|||||
С учетом (1.61) граничное условие (1.55) можно |
|||||||||||||||
представить в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Vуn x, t |
|
h |
x xT |
|
|
V |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(1.62) |
Используя (1.57) и (1.58), равенства (1.б9) и (1.60) |
|||||||||||||||
можно записать как |
|
|
|
|
|
|
|
|
|
|
|
||||
Yб.ц |
|
|
в2 |
h |
V |
xT . |
|
|
|
|
|
(1.63) |
|||
|
|
2 |
|
|
|
|
|
|
1 |
xT |
|
. (1.64) |
|||
Mб.ц |
в |
|
V h xTh V |
|
в |
|
|
|
|
|
|||||
|
|
8 |
в |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так |
как |
h |
и |
|
x |
r |
являются |
нормальными |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ускорениями, то уравнения (1.63) и (1.64) можно также представить в виде
Yб.ц |
|
12 |
в |
2 |
V . |
(1.65) |
11h |
|
|
|
вV |
2 |
|
Mб.ц 12h |
22 |
h V , (1.66) |
||
где 1j - коэффициенты присоединенной массы;
2 j - коэффициенты присоединенного момента инерции.
Из (1.65) и (1.66) видно, что слагаемые, входящие в эти равенства, могут быть объединены с соответствующими слагаемыми в уравнениях возмущенного движения самолета.
23
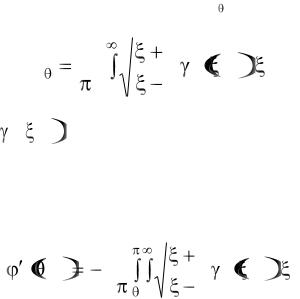
В большинстве случаев эти слагаемые ввиду их малости могут не учитываться [4].
Можно показать [4], что решение уравнения (1.54), полученное за счет распределения по поверхности крыла источников и стоков, хотя и удовлетворяет граничным условиям (1.55), но для точек окружности, соответствующей задней кромке профиля, дает бесконечно большое значение скорости, что противоречит постулату Жуковского - Чаплыгина.
Чтобы обратить в нуль скорость в точке окружности, соответствующей задней кромке, на бесциркуляционный поток необходимо наложить поток от присоединенных вихрей и поток от спутной струи из стекающих вихрей (направление противоположно присоединенным). При этом вихри спутной струи непрерывно удаляются от крыла со скоростью невозмущенного потока. Положение вихрей в спутной струе необходимо выбирать таким образом, чтобы граничные условия (1.55) не нарушались.
Выбранный вихревой слой в произвольной точке окружности индуцирует скорость q , равную
q |
1 |
|
|
в |
|
, t d , |
(1.67) |
|
|
|
|
|
n |
||||
в в |
в |
|||||||
|
|
|
||||||
где n  , t - величина циркуляции, приходящаяся на единицу длины спутной струи.
, t - величина циркуляции, приходящаяся на единицу длины спутной струи.
Этой скорости соответствует следующий потенциал возмущения скорости:
|
, t |
1 |
|
|
в |
|
, t d |
(1.68) |
|
в |
|
|
|
|
n |
||||
2 в |
в |
||||||||
|
|
|
|||||||
24

Подставляя (1.68) в уравнение (1.50) и учитывая антисимметричный характер вихревого течения, получим следующее выражение для разности давлений на верхней и нижней поверхностях крыла:
Pв |
Pн |
|
|
|
|
V |
|
|
|
|
1 cos |
. |
(1.69) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
вsin в |
2 |
в2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
в |
|
cos |
|
|
, t d |
|
|
|
|
|||
|
|
|
n |
|
|
|
|
|||||||
|
|
в |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Интегрирование |
|
(1.69) по |
поверхности крыла |
|||||||||||
единичного размаха приводит к следующим выражениям для подъемной силы и продольного момента крыла относительно
точки x r |
обусловленных циркуляционным течением: |
|
|||||||||||||||||
|
Y |
|
V |
|
|
|
|
|
|
|
|
, t d / 1.70) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ц |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
в |
2 |
в |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Mц |
V |
1 |
|
|
в |
|
xT |
1 |
|
|
|
|
|
. |
(1.71) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
в |
|
в |
2 |
|
|
2 |
в2 |
|||||||||
|
в |
|
|
|
|
|
|
|
|
||||||||||
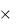 n
n  , t d
, t d
Применение постулата Жуковского - Чаплыгина к объединенному полю скоростей от источников и от вихрей позволяет получить следующее интегральное уравнение, определяющее интенсивность циркуляции спутной струи:
25

1 |
|
|
|
Vyn sin 2 |
|
d |
|
1 |
|
|
|
|
n |
, t d |
0 |
(1.72) |
||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 cos |
2 |
в в |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Подставляя (1.62) в (1.72), можно получить |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
в |
|
, t d |
|
h V |
в |
1 |
|
xT |
|
|
. (1.73) |
||||||
|
|
2 в в |
в n |
|
2 |
|
в |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
, t d |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
в |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. (1.74) |
|
|||||||||||
|
|
|
|
|
вV L в |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Y |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
ц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
, t d |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
в |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
, t d |
(1.75) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
xT 1 |
|
в |
2 |
в |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
M |
ц |
2 |
в |
V L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
в 2 |
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, t d |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
в |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
При гармонических колебаниях |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n x ei t . |
|
|
|
(1.76) |
|
||||||||||||||||||||
|
|
|
Уn |
|
x, t |
|
|
У |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i t . |
|
|
|
(1.77) |
|
|||||||
|
|
|
Vyn |
x, t |
|
|
|
Vyn x e |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
n |
|
, t |
|
|
|
|
|
|
|
|
|
nei |
|
t |
|
|
|
|
|
|
V |
, |
(1.78) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ибо для каждой точки, движущейся вниз по потоку, значение в каждый момент времени постоянно.
26

Равенство (1.78) можно также представить в виде
|
|
|
|
|
|
|
|
|
n , t |
|
|
nei |
t k |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(1.79) |
||||||||
где k |
|
B |
|
является приведенной частотой колебаний, a |
||||||||||||||||||||||
|
V |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
безразмерной координатой. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
С учетом (1.79) отношение интегралов, входящих в |
|||||||||||||||||||||
(1.74) и (1.75), можно представить как: |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
, t d |
|
|
|
|
|
|
|
|
|
|
|
eik |
|
d |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 в2 |
|
1 |
|
|
|
1 |
|
, (1.80) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
в |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
, t d |
|
|
|
|
|
|
|
1 ik |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
в |
n |
|
|
|
|
|
|
|
|
|
e |
d |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
в |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|||||||
т.е. в виде комплексной функции одной лишь приведенной частоты k.
Комплексная функция С(k) носит название функции Теодорсена.
Функция Теодорсена С(k) следующим образом связана с
функциями Ганкеля второго рода [20]: |
|
|
|
||||
C k F k iG k |
|
H12 |
k |
|
|
(1.81) |
|
H 2 |
k |
iH |
2 |
k |
|||
|
|||||||
1 |
|
|
0 |
|
|
||
В свою очередь, функция Ганкеля связана с функциями Бесселя первого и второго рода следующими соотношениями
[22]:
27

Hn2 |
j n iYn . (1.82) |
С учетом (2.80) равенства (2.74) и (2.75) можно представить в виде:
|
|
|
|
|
|
V2 |
|
|
|
|
C k . |
(1.83) |
|||
У |
k |
|
2 |
|
|
|
S |
|
ист |
||||||
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M |
|
|
У |
в |
|
xT |
|
|
1 |
|
C k . |
(1.84) |
|||
|
|
k |
|
к |
|
|
в |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
или в более общем виде: |
|
|
|
|
|
|
|||||||||
|
|
У |
к |
C |
y |
ист |
qSC k . |
(1.85) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Mk |
|
mz |
|
истqSвkC k , |
(1.86) |
||||||||||
где Ук и M к |
- нестационарная подъемная сила и момент |
||||||||||||||
крыла, колеблющегося в несжимаемом потоке газа. |
|||||||||||||||
Из сравнения (1.17), (1.18) с (1.85), (1.86) следует, что |
|||||||||||||||
|
|
|
|
Ук |
|
|
УстC k |
|
|
(1.87) |
|||||
|
|
|
|
Mk |
|
MстC k |
(1.88) |
||||||||
где Уст и Мст - значения подъемной силы и продольного
момента колеблющегося крыла, определенные на основе гипотезы стационарности.
28

Из (1.87) и (1.88) следует, что
C k |
Ук |
|
М к |
. |
Уст |
|
Мст |
||
|
|
|
Таким образом, функция Теодорсена может рассматриваться как амплитудно-фазовая характеристика нестационарных аэродинамических сил и моментов крыла, колеблющегося в несжимаемом потоке газа.
Аналогично может быть получено решение уравнений неустановившегося течения несжимаемого газа для случая, когда имеют место гармонические колебания самого потока, что характерно для движения самолета в турбулентной атмосфере.
Решение этой задачи приведено в [4, 20], где показано, что нестационарные аэродинамические силы и моменты крыла, обтекаемого колеблющимся потоком, можно представить в виде
|
|
|
Ут |
Уст |
k . |
(1.89) |
||
|
|
|
M |
т |
М |
ст |
k , |
(1.90) |
|
|
|
|
|
|
|
||
где У т |
и |
М т |
- |
значения подъемной силы и продольного |
||||
момента крыла, обтекаемого колеблющимся потоком; |
||||||||
Мст |
и |
Уст |
|
- |
значения подъемной силы и продольного |
|||
момента, определенные на основе гипотезы стационарности; k - функция Сирса;
k - приведенная частота колебаний.
Как показано в [3], функция Сирса может быть следующим образом выражена через функцию Теодорсена и функцию Бесселя первого рода:
29
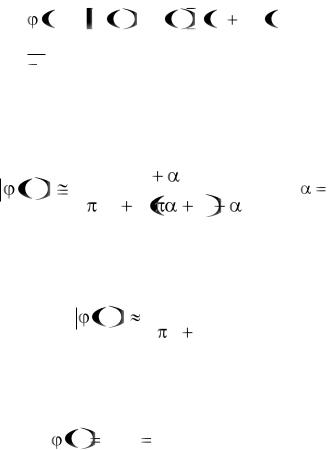
k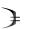 j 0 k - ij 1 k C k
j 0 k - ij 1 k C k ij 1 k
ij 1 k (1.91)
(1.91)
где i 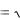
 1.
1.
В работе [3] также показано, что равенство (1.91) может быть аппроксимировано следующим приближенным выражением:
k |
|
2 |
|
k |
|
при |
0,1811 |
|
|
||||||
|
|
2 k2 |
k |
1 |
|||
|
|
|
|
|
|||
|
|
|
|
|
(1.92) |
|
|
или менее точно
k |
|
2 |
|
1 |
|
(1.93) |
|
|
|||||
|
|
|
|
|
||
|
|
2 |
k |
1 |
||
|
|
|||||
Из (1.89) и (1.90) следует, что
k |
Ут |
|
Мт |
(1.94) |
Уст |
|
Мст |
||
|
|
|
т.е. что функция Сирса может рассматриваться как амплитудно-фазовая характеристика аэродинамических сил и моментов крыла, обтекаемого колеблющимся потоком.
1.4. Передаточные функции нестационарных аэродинамических сил и моментов.
Характер обтекания самолета нестационарным потоком подобен характеру обтекания крыла.
30
