Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2294

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.37 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

( k 1)-кратного дифференцирования геометрической прогрессии. При разложении в ряд Лорана иррациональных и трансцендентных функций можно использовать разложения в ряд

Тейлора функций ez ,																					sin z ,				cos z ,							ln 1 z , биномиальный ряд
и другие известные разложения.
																																																1
		Пример 1. Разложить в ряд Лорана функцию																																												f z e							в
		Пример 1. Разложить в ряд Лорана функцию																																												f z e						z	в
окрестности точки z0																					0 .
		Воспользуемся известным разложением
																			eu 1 u										u2						u3	...
																			eu 1 u																	...
																													2!					3!
Положив u									1			, получим:
Положив u									z			, получим:
									z
										1										1				1					1									1
									ez					1						1				1					1					...				1			...
									ez					1														3!z3						...			n!zn				...
																				z 2!z2								3!z3									n!zn
		Пример											2.					Разложить													в				ряд				Лорана								функцию
f z							1								в окрестности точки z0 0 .

				z2		z		6
				z2		z		6
		Функция имеет две особые точки:																																				z1 2 и								z2 3 . Она
аналитична в областях:																							1)		0					z	2 ; 2)							2				z		3; 3)					z		3 .
аналитична в областях:																							1)		0					z	2 ; 2)							2				z		3; 3)					z		3 .
																						f z													f z				1				1				2
Представим функцию																									в виде:																									.
Представим функцию																									в виде:																									.
																																							5	z 3							z	2
		1) В круге													z	2 имеем:
		1) В круге													z	2 имеем:
1					1				1									1						z		z2														z									3),
1					1				1									1						z		z2														z
																					1									... (здесь													1 , т.е.					z
																					1					2				... (здесь													1 , т.е.					z
	z 3				3		1				z							3						3 3																3
							1			3
		1							1					1									1				z				z2														z
		1							1					1									1				z				z2														z
																								1											... (здесь											1, т.е.
									2								z						2	1									2		... (здесь										2	1, т.е.
			z 2						2					1			z						2			2 2																			2
														1			2

z 2 ).

Следовательно,

				1									1								1							1								k											1					1									7
				1									1								1																zk										1					1			z						7		z2 ...
	z	2											5									k 1						2			k 1						zk																		z						27	8	z2 ...
	z		z 6										5								3							2																			6 36														27	8
																k 0
Полученное разложение является рядом Тейлора.
				2) В кольце 2																		z	3 имеем:
				2) В кольце 2																		z	3 имеем:
						1											1				1								1											z				z2				...												3),
																																	1																					(			z
					z 3												3						z						3				1						3					3		2								(			z
					z 3												3		1				z						3										3					3
																			1				3
		1			1					1									1					2					22															1					2					22				... (						2 ).
																				1																	...																										z
																				1												2					...													2							3						z
	z 2 z							1					2						z						z z																			z z											z
								1						z
Следовательно,
													1											1												zk																			2k
													1											1												zk				1												k			2k
																																																													.
								z		2	z								6					5											k 1																			z		k 1					.
								z			z								6					5										3									k 0											z
																										k 0																	k 0
																			z	3 имеем:
				3) В области															z	3 имеем:
								1									1				1						1										3					32															3 ),
																														1															...							(		z
							z																3							1														2	...							(		z
							z				3							z	1				3				z											z					z
																			1				z
		1			1					1									1					2					22															1					2					22				... (						2 ).
																				1																	...																										z
																				1												2					...													2							3						z
	z 2 z							1					2						z						z z																			z z											z
								1				z
Следовательно,
															1								1											3k																				2k
															1								1											3k																	k			2k
																																									1																		.
									z		2												5										z			k 1					1												z		k 1				.
									z					z 6									5										z										k 0										z
																									k 0																		k 0
				Пример									3.						Разложить																		в					ряд							Лорана													функцию
f z sin								z						в окрестности точки																													z0			1 .

						z 1
						z 1

sin

sin 1

sin1 cos

cos1 sin

z 1

cos1

sin1

cos1

1 n

sin1

...

z 1

2! z 1 2

3! z 1 3

2n ! z 1 2n

1 n cos1

2n 1 ! z 1 2n 1 ...

4.4.Изолированные особые точки

Как мы уже знаем, особой точкой функции f z назы-

вается точка, в которой функция не является аналитической. Особая точка z z0 называется изолированной, если в некото-

рой окрестности этой точки функция	f z не имеет других
особых точек.
Если z0 – изолированная особая точка функции f z , то
существует такое число R 0 , что в	кольце 0	z z0	R

функция f z будет аналитической и, следовательно, разлагается в ряд Лорана:

			c k
f z ck z z0	k		c k			.
f z ck z z0			z z	0	k	.
k 0		k 1		0

При этом возможны следующие случаи:

1. Все коэффициенты главной части ряда Лорана равны нулю, т.е. в ряде нет членов с отрицательными показателями:

f z ck z z0 k .

Вэтом случае точка z0 называется устранимой особой точкой

функции f z . Если определить функцию f z в точке z0 ,

положив f z0 lim f z c0 , то функция f z

станет ана-

z z0

литической во всем круге

z z0

R и точка z0

становится

правильной точкой функции

f z .

Изолированная особая точка z z0 является устранимой,

если существует конечный предел lim f z A .

z z0

Пример. Для функции

f z

sin z

точка z0

0 является

особой точкой. Разложение функции

sin z

по степеням z имеет

вид:

sin z

...

Все коэффициенты главной части ряда Лорана равны нулю,

поэтому	точка	z0 0 является	устранимой			особой точкой
функции	f z . Если положить		f 0 lim	sin z		1, то особен-

			z 0	z	f z становится
ность в точке z0		0 устраняется и функция

аналитической во всей комплексной плоскости.

2. Все коэффициенты главной части ряда Лорана, кроме конечного числа, равны нулю, т.е. в ряде Лорана есть конечное число членов с отрицательными показателями:

c n

c n 1

c 1

f z

...

ck z z0

z z

n 1

z z0

k 0

В этом случае точка

z0 называется полюсом кратности n для

функции

f z .

Если

n 1 ,

то точка z0

называется простым

полюсом.

f z можно представить

Если аналитическую функцию

в виде f z z z

n g z ,

где g z 0 , то точка z

называ-

ется нулем кратности n функции f z .

Запишем разложение функции

f z

в ряд Лорана в виде

f z

z z

... c z z

n ... ,

z z0

n 1

или

h z

f z

(4.12)

z z0 n

где h z – аналитическая функция, причем

h z0 c n 0.

Отсюда следует, что

z z0 n

z z0

g z ,

f z

h z

где g z0 1 h z0 1 c n 0 .

Отсюда следует, что если точка z0

– полюс кратности n

для функции

f z ,

то она является нулем кратности n для

функции 1 f z . Справедливо и обратное утверждение: если

точка z0 – нуль кратности n для функции								f z . То она явля-
ется полюсом кратности n для функции 1 f z .
Изолированная особая точка				z z0				является полюсом,
если lim f z .
z z0
Пример 1. Для функции			f z			sin z		особой точкой яв-
							z4

ляется z0 0 . Найдем предел функции при z 0 :
lim	sin z	lim	sin z		1		.

z 0 z4		z 0	z		z3

Следовательно, точка z0 0 является полюсом. Чтобы определить кратность полюса, разложим функцию f z в ряд Ло-

рана в окрестности точки z 0 :
f z	1		z	3		z	5		z	7		1	1	z		z	3

		z									...							...
	4		3!									3	3!z	5!
	z				5!			7!				z			7!

Главная часть ряда Лорана содержит конечное число членов, причем n 3 . Следовательно, точка z 0 – полюс третьего порядка.

Пример	2. Для функции f z	z 3	точки

		z z 2 z 1 2

z1 0 , z2 2	и z3 1 – полюсы, т.к. предел функции во всех

этих точках равен бесконечности. Для определения кратности

полюсов представим функцию

f z

в виде (4.12). Например,

z 3

f z

. Здесь

z z 2

n 2 ,

h z

z 3

, причем

z z 2

z 1 2

h 1

0 . Следовательно,

z 1 –

полюс второго порядка.

Аналогично можно показать, что точки z 0

и z 2 – про-

стые полюсы.

3. Отличны от нуля бесконечное число коэффициентов главной части ряда Лорана, т.е. в ряде есть бесконечно много членов с отрицательными показателями. В этом случае точка

z0 называется существенно особой точкой функции f z .

Можно доказать, что если z0 – существенно особая точка

для функции	f z , то в достаточно малой окрестности точки
z0 функция	f z становится неопределенной. В такой точке

функция не имеет ни конечного, ни бесконечного предела. Это означает, что функция f z стремится к различным пределам,

когда точка z стремится к точке z0 по различным путям. Пример. Для функции f z e1 z точка z0 0 является

особой точкой. Разложение функции e1 z					по степеням z имеет
вид:
e1 z 1	1	1	...	1		...
e1 z 1		z2 2!	...			...
	z	z2 2!		zn n!

Главная часть ряда Лорана содержит бесконечное число членов, следовательно, точка z0 0 является существенно особой

точкой функции e1 z .

Если z 0 вдоль положительной части действительной оси, то 1 z и e1 z . Если z 0 вдоль отрицательной части действительной оси, то 1 z и e1 z 0 . Следовательно, предел функции f z e1 z в точке z 0 не существует.

Классификацию особых	точек можно распространить на
случай, когда особой точкой	функции f z является беско-

нечно удаленная точка. Точка		z является особой точкой
для функции	f z , если точка	z 0 является особой точкой
для функции	f 1 z . Тип особой точки		z для функции
f z совпадает с типом особой точки			z 0 для функции
f 1 z .

5.ТЕОРИЯ ВЫЧЕТОВ

5.1.Вычет функции. Основная теорема о вычетах

Вычетом аналитической функции

f z

в изолирован-

ной особой точке z0

называется комплексное число, равное

значению интеграла

f z dz , взятого в положительном

2 i

направлении по окружности L с центром в точке z0 ,

лежащей

в области аналитичности функции

f z .

Вычет функции

f z

в изолированной особой точке z0

обозначается символом Res f z

или

Res f

z ; z

Таким

образом,

Res f z

f z dz .

(5.1)

2 i

Если в формуле (4.8) положить n 1 , то получим

f z dz или Res f z c ,

(5.2)

2 i

т.е. вычет функции f z относительно особой точки z0

равен

коэффициенту c 1

в разложении этой функции в ряд Лорана в

окрестности точки z0 .

Теорема (основная теорема о вычетах). Если функция f z является аналитической в замкнутой области D, ограни-

ченной контуром L, за исключением конечного числа особых точек zk ( k 1, 2,..., n ), лежащих внутри области D, то

		n
	f z dz 2 i		Res f zk .	(5.3)
L		k 1

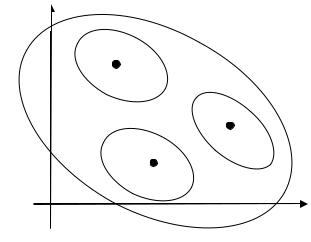
Доказательство. Окружим особые точки z1 , z2 ,..., zn контурами L1, L2 ,..., Ln так, чтобы эти контуры не пересекались между собой и не пересекали контур L (рис. 5.1).

		L
		L1
		z1
		z2
	Ln	zn
		zn
		L2
O		X
		Рис. 5.1
Т.к. функция	f z аналитична в замкнутой области, ле-

жащей между внешним контуром L и внутренними контурами L1, L2 ,..., Ln , то по теореме Коши для сложного контура имеем:

		n			n				n
					2 i
	f z dz			f z dz 2 i		1		f z dz 2 i		Res f zk .
L	f z dz	k 1	Lk	f z dz 2 i	k 1		Lk	f z dz 2 i	k 1	Res f zk .
		k 1			k 1				k 1

Теорема доказана.

5.2. Вычисление вычетов

1. Если z z0 – правильная или устранимая особая точка функции f z , то вычет в этой точке равен нулю, т.к. в разложении в ряд Лорана отсутствует главная часть, поэтому

Res f z0 c 1 0 .

2. Если точка z z0 является простым полюсом функции

f z , то ряд Лорана для функции

f z

в окрестности точки

z0 имеет вид:

c 1

f z

ck z z0

k 0

Отсюда

c 1 z z0 f z ck z z0 k 1 .

k 0

Переходя в этом равенстве к пределу при z z0 , получим:

Res f z

lim z z

f z .

(5.4)

z z0

Пример. Вычислить вычет функции

f z

в осо-

z 2

бой точке z 2 .

Точка z 2 является простым полюсом функции

z 2

Следовательно, в соответствии с (5.4) имеем:

Res f

2 lim z 2

4 .

z 2

Иногда для вычисления вычета в простом полюсе более

удобна другая формула. Пусть функция

f z представлена в

виде f z

, где z

и z

–

функции, аналитиче-

ские в точке z0 , z0 0 , а z имеет простой нуль в точке

z0 (т.е. z0 0 ,	z0 0 ). Тогда в соответствии с (5.4)
имеем:

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.35 Mб12277.pdf
#
15.11.20221.35 Mб12281.pdf
#
15.11.20221.36 Mб02286.pdf
#
15.11.20221.36 Mб12287.pdf
#
15.11.20221.36 Mб02292.pdf
#
15.11.20221.37 Mб12294.pdf
#
15.11.20221.37 Mб32297.pdf
#
15.11.20221.38 Mб42299.pdf
#
15.11.20221.38 Mб02305.pdf
#
15.11.20221.39 Mб02310.pdf
#
15.11.20221.4 Mб12313.pdf