
2292
.pdf
Рис. 11.2
В этом случае для определения постоянной времени проводится огибающая колебательного процесса (пунктир на рис. 11.2), по которой и определяется величина . И в этом случае справедлива формула (11.3).
Постоянная времени зависит от схемы цепи и параметров элементов. Она определяется в результате расчета свободной составляющей переходного процесса.
Например, для цепи первого порядка на рис. 2.1 получено выражение свободной составляющей (2.11) вида (11.1), из которого вытекает выражение для постоянной времени
C |
R1R2 |
. |
(11.5) |
|
|||
|
R1 R2 |
|
|
В последовательном колебательном контуре рис. 2.12 получено выражение для колебательного свободного процесса (2.78), амплитуда которого меняется по закону (11.4). Тогда для постоянной времени получим
|
2L |
. |
(11.6) |
|
|||
|
r |
|
|
Величина постоянной времени характеризует инерционность цепи. Чем она выше, тем медленнее изменяются в цепи свободные токи и напряжения.
171
11.2. Время установления переходного процесса
Теоретически свободные и переходные процессы устанавливаются (протекают) бесконечно долго и строго говоря, время установления переходного процесса бесконечно. Однако подобное определение технически неконструктивно и его необходимо уточнить, введя определенный уровень снижения свободной составляющей переходного процесса, при котором его можно считать практически установившимся.
Например, если принять допустимым снижение свободной составляющей до 1% от начального значения, то из (11.1) получим уравнение для времени установления tу
|
|
S0e tу |
|
S0 |
, |
(11.7) |
||
|
|
|||||||
откуда следует |
|
|
100 |
|
|
|||
1 |
|
4,605 |
|
|
||||
tу |
ln(100) |
4,605 . |
(11.8) |
|||||
|
|
|||||||
Чаще всего используют инженерную оценку времени установления в виде
tу |
(3 5) |
3 5 |
, |
(11.9) |
|
||||
|
|
|
|
|
что вполне согласуется с (11.8).
11.3. Декремент затухания
Для колебательного свободного процесса вида рис. 11.2 в качестве характеристики уменьшения ее амплитуды используется величина декремента затухания, равного отношению амплитуд колебаний A1 и A2 на соседних периодах (отстоящих на интервал периода свободных колебаний T друг от друга в любом месте временной диаграммы),
D |
A1 |
, |
(11.10) |
|
A2 |
||||
|
|
|
как показано на рис. 11.3.
172

Рис. 11.3
При незатухающих колебаниях (в идеальном контуре без потерь) D 1. В реальном контуре при наличии потерь r 0 свободные колебания всегда затухают и D 1. С учетом (11.4) нетрудно показать, что
D |
S |
0 |
e (t T) |
e T . |
(11.11) |
|
S0e t |
||||
|
|
|
|
||
На практике часто удобнее пользоваться логарифми- |
|||||
ческим декрементом затухания d , равным |
|
||||
d ln(D) T . |
(11.12) |
||||
Для простого последовательного колебательного контура вида рис. 2.12 были получены выражения для коэффици-
ента затухания (2.5 б) |
r |
|
|
|||||||
|
|
(11.13) |
||||||||
2L |
||||||||||
|
|
|||||||||
и частоты свободных колебаний (2.65) |
|
|||||||||
|
|
|
|
|
|
|
|
|||
СВ |
|
02 2 |
(11.14) |
|||||||
0 |
|
|
1 |
|
. |
(11.15) |
||||
|
|
|
||||||||
|
||||||||||
|
|
|
|
|
|
LC |
|
|||
Определим период свободных колебаний
173

T |
2 |
|
|
2 |
|
|
|
|
2 |
|
|
, |
(11.16) |
|||
СВ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
r2 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
4Q2 |
|
|||||||||
|
|
|
|
LC |
|
4L2 |
0 |
|
|
|||||||
тогда для логарифмического декремента затухания получим
d T |
|
1 |
|
|
, |
(11.17) |
||||
Q |
|
|
|
|
|
|
||||
|
|
1 |
|
1 |
|
|
|
|
||
|
|
4Q2 |
|
|||||||
|
|
|
|
|
|
|||||
где Q – добротность контура (повторите необходимый мате-
риал). При Q 1 приближенно |
|
||
d |
|
. |
(11.18) |
|
|||
|
Q |
|
|
Как видно, логарифмический декремент затухания полностью определяется добротностью колебательного контура.
Декремент затухания D просто определяется экспериментально по осциллограмме свободного процесса (рис. 11.3) согласно (11.10). Тогда появляется возможность экспериментально определить добротность колебательного контура
спомощью соотношения (11.18).
Ввысокодобротном колебательном контуре свободные колебания затухают медленно, как показано на рис. 11.4 при Q 100. Как видно, измерение декремента затухания затрудни-
тельно ввиду близости значений соседних амплитуд A1 и A2 , что приведет к большой погрешности определения величины
D. Удобнее проводить измерения амплитуд |
A1 и An , разде- |
|||||
ленных n периодами, |
|
|
A1 |
|
|
|
D |
n |
|
, |
(11.19) |
||
A |
||||||
|
|
|
|
|||
|
|
|
n |
|
|
|
(пример для n 10 показан на рис. 11.4).
174

Рис. 11.4
Так как амплитуда свободного процесса затухает экспоненциально (11.4), то нетрудно показать, что
D n D . |
(11.20) |
n |
|
Предлагаемая методика позволяет измерять декремент затухания свободных колебаний в высокодобротном контуре.
11.4. Задания для самостоятельного решения
Задание 11.1. Определите постоянные времени цепей, показанных на рис. 11.5 при выключении идеального источника постоянного входного напряжения uВХ U .
Задание 11.2. Определите время установления переходных процессов для цепей из задания 11.1.
Рис. 11.5
175

Задание 11.3. Определите условия возникновения колебательного режима и частоту свободных колебаний в цепи на рис. 11.6. Получите выражение для декремента и логарифмического декремента затухания.
Рис. 11.6
12.ТРЕХФАЗНЫЕ ЦЕПИ
12.1.Силовая трехфазная сеть переменно тока
Трехфазная силовая сеть представляет собой четырехпроводную систему электропитания, соответствующая «ро-
зетка» показана на рис. |
12.1 а, временные |
диаграммы |
гар- |
монических напряжений |
с частотой f 50 |
Гц между |
фа- |
зами A (uA (t)), B (uB (t)) и C (uC (t)) и нейтралью N приведены на рис. 12.1 б. Напряжения фаз с действующими значениями 220 В (амплитудами U=311 В) сдвинуты друг от друга по фазе на 1200 (на 2 /3 радиан) согласно выражениям
u1(t) U cos( t),
u2 (t) U cos( t 2 /3),u3(t) U cos( t 4 /3).
176
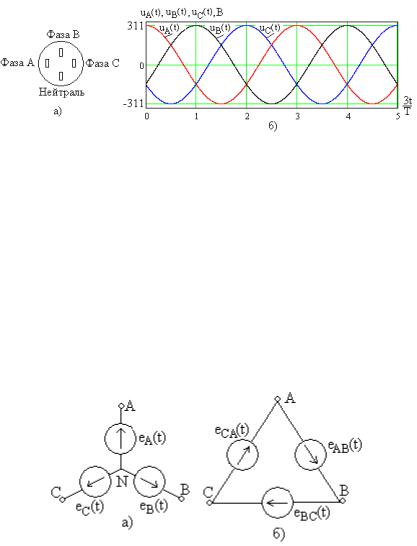
Рис. 12.1
Напряжения между фазами AB (uAB (t)), BС (uBC (t)) и CA (uCA (t)) также имеют гармоническую форму (как и на рис.
12.9б) но с действующим значением 380 В (амплитудой 537 В).
12.2.Модель трехфазной цепи
Модель трехфазной сети (трехфазного источника напряжения) строится из трех идеальных источников напряжения, соединенных «звездой» или «треугольником», как показано на рис. 12.2 а и рис. 12.2 б соответственно.
Рис. 12.2
Нагрузка трехфазной сети (например, обмотки электродвигателя) также включается «звездой» или «треугольником», как показано на рис. 12.3 а и рис. 12.3 б соответственно.
Трехфазный источник (рис. 12.2) и нагрузка (рис. 12.3)
177
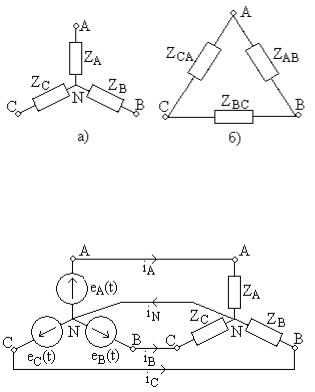
могут соединяться пятью способами:
звезда – звезда;
звезда – треугольник;
треугольник – звезда;
треугольник – треугольник;
звезда – звезда без нейтрали.
Рис. 12.3
Пример соединения «звезда – звезда» показан на рис. 12.4 (остальные варианты схем изобразите самостоятельно).
Рис. 12.4
В модели «звезда» комплексные амплитуды ЭДС источников равны
EA Eej A ,EB Eej B ,EC Eej C ,
при условиях
178

B A 1200, C A 2400
иE 
 2 220 311В , например,
2 220 311В , например,
EA E,EB Eej1200 ,EC Eej2400 .
Очевидно, что
EA EB EC 0.
В модели соединения треугольником (рис. 12.2 б) имеет место аналогичное равенство вида
EAB EBC ECA 0,
то есть кольцевой ток в «треугольнике» отсутствует. Векторная диаграмма ЭДС при соединении звездой по-
казана на рис. 12.5 а.
Трехфазную сеть называют симметричной, если каждая фаза нагружена на одинаковое сопротивление,
ZA ZB ZC .
Рис. 12.5
12.3. Токи и напряжения в трехфазной цепи
Комплексные амплитуды токов фаз в цепи на рис. 12.4
равны
IA EA ,IB EB ,IC EC ,
ZA ZB ZC
В симметричной цепи токи с одинаковыми амплитудами сдвинуты по фазе друг от друга на 1200, их векторная диаграмма при активных сопротивлениях показана на рис. 12.5 б.
179

Если нагрузка комплексна,
ZA ZB ZC Zej ,
Z – модуль, а – аргумент сопротивления нагрузки (сдвиг фаз между напряжением и током фазы), то диаграмма токов будет отличаться от показанной на рис. 12.5 б поворотом на угол по часовой стрелке. Аналогичная векторная диаграмма для соединения треугольником резистивно-индуктивных нагрузок показана на рис. 12.5 в.
По первому закону Кирхгофа (рис. 12.4 б) сумма токов фаз равна току нейтрали
IA IB IC IN ,
а при симметричной нагрузке ток нейтрали равен нулю,
IA IB IC 0.
При асимметрии нагрузки в трехфазной сети появляется ток нейтрали. На практике его значение в несколько раз меньше токов фаз.
В трехфазном источнике фазные напряжения формируются на нагрузках, например, обмотках электродвигателя (катушках индуктивности). Источник соединен с нагрузкой проводными линиями, например, как показано на рис. 12.4. Напряжения между линиями фаз называют линейными.
При включении обмоток звездой (рис. 12.14 а) напряжения между соответствующей фазой и нейтралью равны фазным напряжениям генератора UA,UB ,UC с действующими
значениями UФ =220 В. Линейными напряжениями в этом случае являются UAB ,UBC ,UCA , их действующие значения
одинаковы и определяется из векторной диаграммы на рис. 12.5 а,
|
2 cos(300 ) UФ |
|
|
|
|
|
UAB UBC UCA |
3 UФ , |
|||||
UФ 220В получим UAB |
UBC UCA |
|
3 |
220 380В. По |
||
этой причине однофазную силовую сеть (одна из фаз и нейтраль) называют сетью 220В, а трехфазную – сетью 380 В.
180
