2024

индекс (или индексы) элемента матрицы. Например, таким образом можно присваивать новые значения элементам, переопределяя тем самым исходную матрицу (рис. 24). При этом надо помнить, что по умолчанию индексация начинается с 0, т. е. первый элемент матрицы имеет номер 0, второй 1 и т. д. Чтобы перейти в режим ввода нижних индексов, надо

нажать пиктограмму 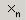на панели Matrix.

Для того чтобы выделить отдельный столбец матрицы, можно использовать пиктограмму 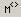. Чтобы выделить строку, можно применить этот же оператор к транспонированной матрице.

Рис. 23. Диалоговое окно Вставка матрицы

Рис. 24. Обращение к элементам матрицы

81

Простейшие операции с матрицами (сложение, умножение) выполняются с помощью соответствующих операторов (А + B, A * B). Для выполнения других операций (транспонирование, вычисление определителя, обратной матрицы и т. д.) можно использовать пиктограммы на панели

Matrix.

Кроме этого, в Mathcad есть следующие группы основных встроенных функций для работы с матрицами:

1) функции для разбиения и слияния матриц: submatrix(A, ir, jr, ic, jc) – выделяет из матрицы А

подматрицу, заключенную между строками ir и jr и стобцами ic и jc включительно;

augment(A, B, C,…) – выполняет слияние указанных матриц слева направо;

stack(A, B, C,…) – выполняет слияние указанных матриц сверху вниз;

2) функции вычисления различных числовых характеристик матриц:

rows(A) – возвращает количество строк в матрице А; cols(A) – возвращает количество столбцов в матрице А; length(V) – возвращает число элементов вектора V; max(A) – возвращает максимальный элемент в матрице

А;

min(A) – возвращает минимальный элемент в матрице

А;

mean(A) – вычисляет среднее значение элементов матрицы А.

Примеры использования функций приведены на рис. 25.

82

Таблица 12

Значения коэффициентов для функции взять из табл. 14.

84

85

Задание 4. Задать матрицы А и В. Найти сумму, произведение матриц, их определители, транспонированные и обратные матрицы, применить к ним основные встроенные функции для работы с матрицами.

4.УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ОТЧЕТА

Отчет должен содержать:

- наименование и цель работы; - краткие теоретические сведения;

- задание на лабораторную работу; - результаты выполнения лабораторной работы.

5.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Какие математические панели инструментов есть в Mathcad, для чего они предназначены?

2.Как в Mathcad определить какую-либо переменную, как потом узнать ее значение?

3.Что такое дискретная переменная, как она задается в

Mathcad?

4.Как можно построить в Mathcad график кусочнонепрерывной функции и график поверхности?

5.Какие функции есть в Mathcad для работы с матрицами?

86

Лабораторная работа № 2 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

СПОМОЩЬЮ MATHCAD

1.ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ

1.1.Цель работы

Изучение основных методов решения систем линейных уравнений; получение практических навыков написания функций на встроенном в Mathcad языке программирования.

1.2.Используемое оборудование и программное обеспечение

Для выполнения лабораторной работы требуется ПЭВМ типа IBM PC с установленной ОС Windows XP и выше, математический пакет Mathcad 14 и выше.

2.МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ

2.1. Встроенные инструменты Mathcad для решения систем линейных уравнений

Для решения систем линейных уравнений в среде Mathcad есть специальная функция lsolve(A, B), которая по матрице коэффициентов и вектору правых частей уравнений позволяет определить вектор неизвестных (рис. 26).

Еще одним способом решения уравнений и их систем является использование вычислительного блока Given/Find, который задается следующим образом:

Given – ключевое слово,

система уравнений, записанная с помощью логических операторов;

Find(var1, var2,…) – встроенная функция, производящая поиск значение неизвестных var1, var2,…, удовлетворяющих условиям, записанным в вычислительном блоке.

87

Логические операторы внутри блока Given/Find вводятся с помощью панели инструментов Булева алгебра.

Рис. 26. Решение системы уравнений с помощью функции lsolve()

Пример решения системы линейных уравнений с помощью вычислительного блока Given/Find приведен на рис. 27.

Рис. 27. Пример решения системы линейных уравнений с помощью блока Given/Find

88

Особенностью блока Given/Find является необходимость задания начального приближения.

2.2. Примеры реализации численных методов решения систем линейных уравнений в Mathcad

При решении систем линейных уравнений часто возникают задачи преобразования матриц. Большая часть численных алгоритмов, выполняющих такие преобразования, реализована в Mathcad в виде встроенных функций. К наиболее популярным функциям, используемым для решения задач линейной алгебры, относятся:

rref(A) – выполняет приведение матрицы А к верхнему треугольному виду;

eigenvals(A) – вычисляет собственные значения квадратной матрицы А;

eigenvecs(A) – вычисляет собственные вектора квадратной матрицы А;

lu(A) – выполняет разложение матрицы A C L U , где L и U – соответственно, верхняя и нижняя треугольные матрицы;

cholesky(A) - выполняет разложение матрицы по схеме

Холецкого A L LT , где L – верхняя треугольная матрица; norm1(A) – выполняет вычисление первой

(неопределенной) нормы матрицы А;

normi(A) – вычисляет бесконечную норму матрицы А; norme(A) – определяет евклидову норму матрицы А. Рассмотрим пример реализации в Mathcad метода Гаусса для решения системы линейных уравнений. Для этого составим расширенную матрицу, присоединив к матрице A вектор правых частей В, и приведем ее к треугольному виду,

выполнив таким образом прямой ход метода Гаусса:

89

Далее преобразуем расширенную матрицу так, чтобы в первых n столбцах получилась единичная матрица (обратный ход метода Гаусса):

Последний (n 1)-й столбец этой матрицы содержит решение системы. Пример кода Mathcad приведен на рис. 28.

Рис. 28. Решение системы уравнений методом Гаусса

Рассмотрим пример реализации в Mathcad метода простой итерации (рис. 29).

90