
2024
.pdfДля того чтобы выделить из семейства решений дифференциального уравнения одно конкретное решение, задают дополнительные условия, количество которых равно порядку уравнения. В качестве дополнительных условий могут задаваться значения искомой функции и ее производных при некоторых значениях независимой переменной, т.е. в некоторых точках.
Если эти условия задаются в одной точке, то такая задача называется задачей Коши, сами дополнительные
условия называются начальными, |
а точка x x0 , в которой |
|||
они задаются, - начальной точкой. |
|
|
||
Например, задача Коши для дифференциального |
||||
уравнения |
первого |
порядка |
y f(x,y) |
формулируется |
следующим |
образом: |
для заданных x0,y0 |
найти такое |
|
решение y y(x), при котором y(x0) y0.
Если же для уравнения порядка n 1 дополнительные условия задаются в более чем одной точке, т.е. при разных значениях независимой переменной, то такая задача называется краевой, а сами условия называются граничными (или краевыми) условиями. На практике обычно граничные условиях задаются в двух точках x a и x b, являющихся границами отрезка, на котором рассматривается дифференциальное уравнение.
5.2. Численные методы решения задачи Коши
5.2.1. Метод Эйлера
Сформулируем задачу Коши следующим образом: найти функцию Y Y(x), удовлетворяющую уравнению
Y f(x, Y)
и принимающую при x x0 заданное значение Y0: Y(x0) Y0.
61

Для решения задачи Коши чаше всего используются
разностные методы.
Введем последовательность точек x0,...,xn и шагов
между ними hi xi 1 xi (i 0,...,n 1). В каждой точке xi , называемой узлом, вместо значений непрерывной функции Y(xi ) вводятся числа yi , аппроксимирующие точное решение Y на данном множестве точек. Дискретную функцию y, заданную в виде таблицы {xi,yi}, называют сеточной функцией.
Простейшим численным методом решения задачи Коши для обыкновенного дифференциального уравнения является
метод Эйлера.
Рассмотрим уравнение Y f(x,Y) в окрестностях узлов x xi и заменим в левой части производную Y правой разностью. При этом значения функции Y в узлах xi заменим значениями сеточной функции yi :
yi 1 yi f(xi,yi). hi
Будем считать для простоты узлы равноотстоящими. т.е. hi xi 1 xi h const . Тогда получаем
yi 1 yi hf(xi,yi), |
i 0,1,... |
Полагая i 0, находим значение сеточной функции y1
при x x1:
y1 y0 hf(x0,y0).
Требуемое здесь значение y0 задано начальным условием, т.е.
y0 Y0.
Аналогично могут быть найдены значения сеточной функции в других узлах:
62
y2 y1 hf(x1,y1),
...
yn yn 1 hf(xn 1,yn 1).
Поскольку для вычисления значения сеточной функции yi 1 используется только ее значение yi в предыдущем узле xi , то метод Эйлера является одношаговым.
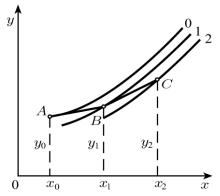
Геометрическая интерпретация метода Эйлера приведена на рис. 10, где показаны первые два шага, т.е. вычисление сеточной функции y в точках x1 и x2 . Интегральные кривые 0, 1, 2 описывают точное решение исходного уравнения Y f(x, Y), при этом кривая 0 соответствует точному решению задачи Коши, поскольку она проходит через точку A с координатами (x0,y0). Точки В и С
получены в результате первого и второго шагов метода Эйлера. Как видно, в процессе вычислений происходит переход с одной интегральной кривой на другую, и полученное решение все дальше отклоняется от истинного.
Рис. 10. Геометрическая интерпретация метода Эйлера
Таким образом, метод Эйлера является простым одношаговым методом решения задачи Коши, но его практическое применение ограничивается большой
63
погрешностью вычислений. Как правило, он используется только в тех случаях, когда высокая точность решения не требуется.
Пример. Решить задачу Коши
Y 2(x2 Y), |
Y(0) 1, |
0 x 1, |
h 0.1. |
Произведем вычисления по схеме Эйлера:
y1 y0 hf(x0,y0) 1 0.1 2 (02 1) 1.2, y2 y1 hf(x1,y1) 1.2 0.1 2 (0.12 1.2) 1.442,
...
Занесем все вычисления в табл. 10 и для сравнения добавим в нее столбцы с решением, полученным с помощью метода Рунге-Кутта, который будет рассмотрен далее, и точное решение, вычисленное с использованием методов высшей математики.
|
|
|
Таблица 10 |
|
|
|
|
|
|
xi |
Метод |
Метод Рунге- |
Точное |
|
Эйлера |
Кутта |
решение |
|
|
0.1 |
1.2000 |
1.2221 |
1.2221 |
|
0.2 |
1.4420 |
1.4977 |
1.4977 |
|
0.3 |
1.7384 |
1.8432 |
1.8432 |
|
0.4 |
2.1041 |
2.2783 |
2.2783 |
|
0.5 |
2.5569 |
2.8274 |
2.8274 |
|
0.6 |
3.1183 |
3.5201 |
3.5202 |
|
0.7 |
3.8139 |
4.3927 |
4.3928 |
|
0.8 |
4.6747 |
5.4894 |
5.4895 |
|
0.9 |
5.7377 |
6.8643 |
6.8645 |
|
1.0 |
7.0472 |
8.5834 |
8.5836 |
|
Как видно, погрешность метода Эйлера возрастает при каждом вычислении значения сеточной функции в узле xi .
64
5.2.2. Метод Рунге-Кутта
Одношаговый метод Эйлера является частным случаем методов Рунге-Кутта, использующих для вычисления значения yi 1 не только yi , но и значения функции f(x,y) при некоторых специальным образом выбираемых x [xi,xi 1] и y.
Рассмотрим метод Рунге-Кутта четвертого порядка.
Запишем алгоритм этого метода в виде |
|
|
|
|
|
||||||||
|
yi 1 yi |
h |
(k0 2k1 2k |
2 k3), |
i 0,1,..., |
||||||||
|
|
||||||||||||
|
6 |
|
|
|
|
h |
|
h |
|
||||
|
k0 f(xi,yi), |
k1 f(xi |
|
,yi |
k0), |
||||||||
|
|
2 |
|||||||||||
|
|
h |
|
|
|
h |
|
2 |
|
|
|||
k2 |
f(xi |
,yi |
k1), k3 |
f(xi h,yi hk2). |
|||||||||
|
2 |
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||
Таким образом, данный метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части f(x,Y) исходного дифференциального уравнения.
Метод Рунге-Кутта требует большего объема вычисления по сравнению с методом Эйлера, однако это окупается повышенной точностью, что дает возможность проводить счет с большим шагом. Другими словами, для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе Рунге-Кутта.
Пример. Решить задачу Коши
|
|
Y 2(x2 Y), |
Y(0) 1, |
0 x |
1, h 0.1. |
|||||||||||
|
|
Для вычисления значения y1 |
|
вначале |
|
определим |
||||||||||
коэффициенты k0 k3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0.1 |
|
2 |
|
|
0.1 |
|
|
|
|
k |
0 |
2(02 1) 2, k |
1 |
2 |
|
0 |
|
|
|
1 |
|
|
2 |
|
2.205, |
|
2 |
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65

|
|
|
|
|
0.1 2 |
|
0.1 |
|
|
|
|
||
k |
2 |
2 |
|
0 |
|
|
1 |
|
|
2.205 |
|
|
2.2255, |
|
2 |
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k3 2 0 0.1 2 1 0.1 2.2255 2.4651,
y1 1 0.1 2 2 2.205 2 2.2255 2.4654 1.2221. 6
Результаты остальных итераций приведены в табл. 10. Как видно, решение, полученное с помощью метода РунгеКутта, гораздо более близко к точному, чем вычисления по схеме Эйлера.
Контрольные вопросы
1.Как формулируется задача Коши? Какова ее геометрическая интерпретация?
2.Что такое сеточная функция? Зачем она используется?
3.В чем заключается метод Эйлера решения задачи Коши? Какие преимущества и недостатки имеет данный метод?
4.Чем метод Рунге-Кутта отличается от метода Эйлера? Какие преимущества и недостатки есть у метода Рунге-Кутта?
Задания для самостоятельной работы
Решить задачу Коши с помощью метода: а) Эйлера; б) Рунге-Кутта:
5.1. y xy2, |
y(0) 1, |
0 x 1, |
h 0.1. |
|
5.2. y x y, |
y(0) 0, |
0 x 1, |
h 0.1. |
|
5.3. y sin(x) cos(y), |
y(0) 1, |
0 x 1, |
h 0.1. |
|
66
Лабораторная работа № 1 ЗНАКОМСТВО СО СРЕДОЙ MATHCAD
1.ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
1.1.Цель работы
Изучение основных принципов работы с переменными
ифункциями в среде Mathcad; получение практических навыков построения декартовых и трехмерных графиков.
1.2.Используемое оборудование и программное обеспечение
Для выполнения лабораторной работы требуется ПЭВМ типа IBM PC с установленной ОС Windows XP и выше, математический пакет Mathcad 14 и выше.
2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
2.1. Назначение среды Mathcad
Mathcad – программное средство, среда для выполнения разнообразных математических и технических расчетов, предоставляющая пользователю инструменты для работы с формулами, числами, графиками и текстами, снабженная простым в освоении графическим интерфейсом.
В среде Mathcad доступны более сотни операторов и логических функций, предназначенных для численного и символьного решения технических задач различной сложности. В состав Mathcad входят несколько интегрированных между собой компонентов:
-мощный текстовый редактор, позволяющий вводить, редактировать и форматировать как текст, так и математические выражения;
-обширная библиотека встроенных математических функций;
-инструменты построения графиков различных типов;
67
-встроенный язык программирования, позволяющий создавать функции для решения задач, которые невозможно или очень сложно решить стандартными инструментами пакета;
-удобная справочная система.
2.2. Графический интерфейс пользователя
После запуска Mathcad появляется главное окно приложения, показанное на рис. 11. Оно имеет ту же структуру, что и большинство приложений Windows. Сверху вниз располагаются заголовок окна, строка меню, панели инструментов и рабочая область. В самой нижней части окна находится строка состояния.
Рис. 11. Рабочее окно приложения Mathcad
Помимо элементов управления, характерных для типичного текстового редактора, Mathcad снабжен дополнительными средствами для ввода и редактирования математических символов (рис. 12).
68
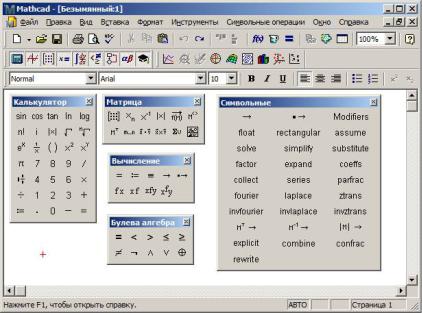
Рис. 12. Основные и математические панели инструментов
Mathcad
Перечислим назначение математических панелей инструментов:
-Математика - предназначена для вызова на экран остальных панелей, с помощью который и происходит вставка математических операций в документы; чтобы вызвать какуюлибо их них, нужно нажать соответствующую кнопку на панели Математика;
-Калькулятор – служит для вставки основных математических операций;
-График – для вставки графиков;
-Вектор и матрица – для вставки матриц и матричных операторов;
-Вычисления – для вставки операторов управления вычислениями;
-Математический анализ – для вставки операторов интегрирования, дифференцирования, суммирования;
69
-Булева алгебра – для вставки логических (булевых) операторов;
-Программирование – для программирования средствами Mathcad;
-Греческие символы – для вставки греческих символов;
-Символьные преобразования – для вставки символьных операторов.
2.3. Основы работы с документами в Mathcad
2.3.1. Работа с числами и функциями
После запуска приложения открывается пустое рабочее окно. Все команды пользователя выполняются именно в нем. Команды вводятся в месте размещения указателя в рабочей области. Изменить его положение на рабочем листе можно либо щелчком мыши, либо с помощью клавиш управления курсором.
Команды пользователя могут вводиться с клавиатуры, выбором команд (или их пиктограмм) на панелях меню или с помощью нажатия комбинаций клавиш. Последний способ является очень удобным, т. к. позволяет быстро задавать необходимые команды без их поиска. Наиболее часто используемые команды, панели инструментов, на которых они расположены, и соответствующие им пиктограммы и сочетания клавиш приведены в табл. 11.
Для выполнения арифметических операций в Mathcad используются стандартные математические операторы (+, -, *, /). Эти операторы обычно вводятся непосредственно с помощью клавиатуры, однако их же можно ввести при помощи пиктограмм панели инструментов Калькулятор.
При вводе операторов в рабочем документе в области ввода автоматически появляются структурные заполнители, вместо которых и вводятся числа или символы.
70
