2024

Задания для самостоятельной работы

Найти решение нелинейного уравнения на заданном интервале с точностью 0.01 с помощью метода половинного деления, метода хорд и метода Ньютона. Сравнить методы по числу итераций, за которые получено решение:

41

3. МЕТОДЫ АППРОКСИМАЦИИ ФУНКЦИЙ

3.1. Постановка задачи аппроксимации функций

Вычисление значения функции y f(x) - одна из самых распространенных задач, с которой постоянно приходится сталкиваться при проведении как научных, так и прикладных исследований. Если функция f(x) задана аналитически и является относительно простой, то ее вычисление не вызывает никаких проблем. Однако непосредственное вычисление функции затруднено в следующих ситуациях:

1) функция f(x) задана таблицей из n своих значений

проведением сложных расчетов и приводит к значительным затратам времени или вычислительных ресурсов, которые могут оказаться неприемлемыми, если функция f(x) нужно считать многократно или значение f(x) надо получить быстро;

3) значения функции f(x) находятся из эксперимента и, скорее всего, содержат ошибки эксперимента.

В таких случаях функцию f(x) приближенно заменяют более простой функцией (x), которая может быть быстро и надежно вычислена. В зависимости от критерия выбора функции (x) выделяют несколько типов задач поиска приближенных значений функции.

Если необходимо функцию f(x) приближенно заменить функцией (x) так, чтобы отклонение (x) от f(x) в заданной области было минимальным, то решается задача

42

Если необходимо, чтобы приближенная функция (x)

совпадала с функцией f(x) на заданном множестве точек xi ,

осуществляется интерполяция функции. Если необходимо найти значение функции f(x) в точке x, не принадлежащей

отрезку [x1, xn], то решается задача экстраполяции функции. Этот метод приближения часто используется для прогнозирования характера протекания тех или иных процессов при значениях параметров x, выходящих за пределы отрезка наблюдения. Надежность такого прогноза при значениях x, отдаленных на значительное расстояние от отрезка [x1, xn], как правило, невелика.

Для построения приближенной функции (x) применяются такие методы, как разложение функции f(x) в ряды, замена функции многочленом и т.п.

3.2. Линейная и квадратичная интерполяция

Простейшим видом интерполяции является линейная интерполяция. Она состоит в том, что заданные точки (xi,yi)

(xi,yi).

Для построения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. Запишем уравнение прямой, проходящей через точки (xi 1,yi 1) и (xi,yi), в следующем виде:

y yi 1 x xi 1 .

43

Отсюда

ai yi yi 1 , bi yi 1 aixi 1.

Если задано n узлов интерполяции, то надо построить (n 1) таких уравнений.

При квадратичной (или параболической) интерполяции

в качестве интерполяционной функции на отрезке (xi 1,xi 1)

Для определения неизвестных коэффициентов ai,bi,ci запишем три уравнения, означающие условия прохождения параболы через точки (xi 1,yi 1), (xi,yi) и (xi 1,yi 1):

aixi2 1 bixi 1 ci yi 1,

aixi2 bixi ci yi,

aixi2 1 bixi 1 ci yi 1.

Пример. Функция y f(x) задана таблицей значений

bi yi 1 aixi 1 3.63 14.4 0.30 0.69, y 14.4x 0.69 14.4 0.32 0.69 3.92.

44

Теперь воспольуемся формулой квадратичной интерполяции. Составим систему уравнений с учетом ближайших к точке x 0.32 узлов xi 1 0.15, xi 0.30,

xi 1 0.40:

0.152ai 0.15bi ci 2.17,

0.302ai 0.30bi ci 3.63, 0.402ai 0.40bi ci 5.07.

Решая эту систему, находим ai 18.67, bi 1.33, ci 1.55. Тогда искомое значение функции

y18.67 0.322 1.33 0.32 1.55 3.89.

3.3.Многочлен Лагранжа

Наиболее простым и исследованным случаем интерполяции является замена исходной функции, заданной

многочленом Pn(x) aixi , таким, что Pn(xi) yi .

i 1

Такому требованию удовлетворяет интерполяционный многочлен Лагранжа. Запишем его в виде

n

Ln(x) yili(x) y0l0(x) y1l1(x) ... ynln (x),

i 1

где

Наиболее часто используется многочлен Лагранжа первой, второй и третьей степени. Запишем формулы многочлена первой и второй степени:

45

46

y0 y1 y0,y1 y2 y1,

...

yn 1 yn yn 1.

Эти значения называют конечными разностями первого порядка. Разности второго порядка определяются следующим образом:

2y0 y1 y0,2y1 y2 y1,

...

2yn 2 yn 1 yn 2.

Аналогично разности k-го порядка вычисляются по формуле

Запишем формулу для многочлена Ньютона в следующем виде

... ny0 t t 1 ... t n 1, n!

где t (x x0)/ h.

Данное выражение называется первым многочленом Ньютона для интерполирования вперед. Оно может аппроксимировать функцию y f(x) на всем отрезке [x0,xn ],

однако, с точки зрения повышения точности расчетов более целесообразно использовать первый многочлен Ньютона для вычисления значений функции в точках левой половины рассматриваемого отрезка.

47

Для правой половины отрезка [x0,xn ] разности лучше

... ny0 q q 1 ... q n 1, n!

где q (x xn )/h.

Пример. Вычислить в точке x 0.1 значение функции,

Конечные разности вычислены следующим образом:

y0 y1 y0 4.465 1.272 3.193,y1 y2 y1 5.644 4.465 1.179,

...

2y0 y1 y0 1.179 3.193 2.014,

...

5y0 4y1 4y0 3.000 ( 1.999) 4.999.

48

Подставим в формулу для первого многочлена Ньютона полученные конечные разности и значение x 0.1:

t (x x0)/ h (0.1 0)/0.2 0.5,

N(0.1) 1.272 3.193 0.5 2.0140.5 0.5 1 1! 2!

1 0.5 0.5 1 0.5 2 1.9990.5 0.5 1 0.5 2 0.5 3 3! 4!

.4.9990.5 0.5 1 0.5 2 0.5 3 0.5 4 3.398. 5!

Теперь используем для нахождения значения функции второй многочлен Ньютона:

q (x xn )/h (0.1 1)/0.2 4.5,

N(0.1) 2.101 ( 1.860) ( 4.5) 0.012( 4.5) 4.5 1 1! 2!

2.001( 4.5) 4.5 1 4.5 2 3!

3.000( 4.5) 4.5 1 4.5 2 4.5 3 4!

.4.999( 4.5 4.5 1 4.5 2 4.5 3 4.5 4 3.402. 5!

Контрольные вопросы

1. В каких ситуациях возникает необходимость замены функции на приближенную? Какие существуют виды аппроксимации функции?

3.В чем заключается линейная и квадратичная интерполяция?

4.Какому требованию должен отвечать интерполяционный многочлен?

5.В каких случаях лучше использовать интерполяционный многочлен Лагранжа, первый и второй интерполяционные многочлены Ньютона?

49

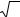
Задания для самостоятельной работы

С помощью многочлена Лагранжа определить значение функции в точке x 10.

3.2. С помощью многочлена Лагранжа определить

50