
2024
.pdf4. МЕТОДЫ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
4.1. Постановка задачи интегрирования функции
В прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла
b
I a f(x)dx.
Если функция f(x) задана аналитически и непрерывна на отрезке [a,b], то для вычисления интеграла можно использовать формулу Ньютона-Лейбница:
b
a f(x)dx F(b) F(a).
где F(a) и F(b) - значения первообразной функции f(x) в точках a и b, соответственно.
Однако на практике получить значение интеграла с помощью данной формулы затруднительно по двум причинам:
- вид функции f(x) не допускает непосредственного интегрирования, т.е. первообразную F(x) нельзя выразить через элементарные функции;
- функция f(x) задана таблично.
В этих случаях используют приближенные методы интегрирования, основанные на аппроксимации подынтегральной функции некоторыми более простыми выражениями, например, степенным рядом или интерполяционным многочленом.
Геометрически определенный интеграл можно интерпретировать как площадь криволинейной трапеции,
ограниченной графиком функции f(x), осью x |
и прямыми |
||
x a , x b (рис. 3). |
|
|
|
Разобьем отрезок [a,b] |
на элементарные отрезки |
||
[xi 1,xi] точками |
a x0 x1 |
... xn b. |
Интеграл I |
разобьется при этом |
на сумму элементарных интегралов |
||
51
|
n |
|
I Ii, |
|
i 1 |
xi |
|
где Ii xi 1 |
f(x)dx , что соответствует разбиению площади |
исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций (рис. 4).
y
y=f(x)
a |
b |
x |
Рис. 3. Геометрическая интерпретация определенного интеграла
y
y=f(x)
a=x0 x1 x2 x3 |
… |
xn=b |
x |
Рис. 4. Замена криволинейной трапеции суммой элементарных трапеций
52

4.2. Метод прямоугольников
Метод прямоугольников является простейшим методом численного интегрирования. Он основан на замене площади элементарной криволинейной трапеции прямоугольником, основанием которого является отрезок [xi 1,xi], а в качестве высоты выбирается значение функции в одной из границ отрезка или в его середине.
В зависимости от выбора точки измерения высоты прямоугольника различают несколько вариантов метода:
1) метод левых прямоугольников (рис. 5) предполагает вычисление интеграла по следующей формуле:
b |
n 1 |
|
f(x)dx h f(xi), |
||
a |
||
|
i 0 |
где h xi xi 1, для простоты примем h const ;
y
y=f(x)
a=x0 x1 x2 x3 |
… |
xn=b |
x |
Рис. 5. Графическая иллюстрация метода левых прямоугольников
2) метод правых прямоугольников (рис. 6) для вычисления определенного интеграла использует формулу
b |
n |
|
f(x)dx h f(xi), |
||
a |
||
|
i 1 |
53
y
y=f(x)
a=x0 x1 x2 x3 |
… |
xn=b |
x |
Рис. 6. Графическая иллюстрация метода правых прямоугольников
3) метод центральных (или средних) прямоугольников
(рис. 7) предполагает измерение высоты в середине отрезка
[xi 1,xi]:
|
b |
n |
|
a f(x)dx h f(xi 1/ 2), |
|
|
|
i 1 |
где xi 1/ 2 |
(xi xi 1)/2, i 1,...,n. |
|
y |
y=f(x) |
|
a=x0 x1 x2 x3 |
… |
xn=b |
x |
Рис. 7. Графическая иллюстрация метода центральных прямоугольников
54
|
|
|
|
1 |
dx |
|
|
Пример. Вычислить определенный интеграл I |
|
|
|
||||
1 x |
2 |
|
|||||
с помощью метода прямоугольников. |
|
0 |
|
|
|||
|
|
|
|
|
|||
Разобьем |
отрезок |
интегрирования [0, 1] |
на десять |
||||
равных частей: |
n 10, |
h 0.1. |
Вычислим |
значения |
|||
подынтегральной функции |
yi 1 1 xi2 |
в точках разбиения |
|||||
xi , а также в полуцелых точках xi 1/ 2, i 1,...,n (табл. 9).
|
|
|
|
Таблица 9 |
|
|
|
|
|
|
|
i |
xi |
yi |
xi 1/ 2 |
yi 1/ 2 |
|
0 |
0.0 |
1.000000 |
- |
- |
|
1 |
0.1 |
0.990099 |
0.05 |
0.997506 |
|
2 |
0.2 |
0.961538 |
0.15 |
0.977995 |
|
3 |
0.3 |
0.917431 |
0.25 |
0.941176 |
|
4 |
0.4 |
0.862069 |
0.35 |
0.890868 |
|
5 |
0.5 |
0.800000 |
0.45 |
0.831601 |
|
6 |
0.6 |
0.735294 |
0.55 |
0.767754 |
|
7 |
0.7 |
0.671141 |
0.65 |
0.702988 |
|
8 |
0.8 |
0.609756 |
0.75 |
0.640000 |
|
9 |
0.9 |
0.552486 |
0.85 |
0.580552 |
|
10 |
1.0 |
0.500000 |
0.95 |
0.525624 |
|
Используем для вычисления все три модификации метода прямоугольников:
1) формула левых прямоугольников
I1 0.1 1 0.99099 0.961538 ... 0.552486 0.810071; 2) формула правых прямоугольников
I2 0.1 0.99099 0.961538 ... 0.552486 0.5 0.760071; 3) формула центральных прямоугольников
I3 0.1 0.997506 0.977995 ... 0.525624 0.785606.
55
Истинное значение интеграла легко определяется по формуле
I arctg|01 0.785398. 4
Как видно, ближе всего к правильному решению оказалось значение I3 , вычисленное по формуле центральных прямоугольников.
4.3. Метод трапеций
Метод трапеций использует линейную интерполяцию, т.е. график функции y f(x) представляется в виде ломаной,
соединяющей точки (xi,yi). В этом случае площадь криволинейной трапеции приближенной заменяется суммой площадей элементарных прямолинейных трапеций (рис. 8).
y
y=f(x)
a=x0 x1 x2 x3 … xn=b x
Рис. 8. Графическая иллюстрация метода трапеций
Площадь элементарной трапеции равна произведению полусуммы оснований на высоту:
si |
|
yi 1 yi |
h, |
i 1,...,n. |
|
||||
|
2 |
|
|
|
С учетом этого соотношения формула трапеций для численного интегрирования имеет вид:
56
b |
h |
n |
|
|
yn |
n 1 |
|
|
|
|
|
yi 1 |
|
y0 |
|
|
|
|
|||
f(x)dx |
|
yi h |
|
yi . |
|
|
||||
a |
2 i 1 |
|
|
2 |
i 1 |
|
|
|
||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
dx |
|
Пример. Вычислить определенный интеграл I |
|
|
||||||||
1 x |
2 |
|||||||||
|
|
|
|
|
|
|
|
0 |
|
|
с помощью метода трапеций.
Подставим в формулу трапеций значения функции из табл. 9.
|
1 0.5 |
|
|
|
||
I4 |
0.1 |
|
0.990099 ... 0.552489 |
|
0.784981. |
|
2 |
||||||
|
|
|
|
|
||
4.4. Метод Симпсона
Разобьем отрезок интегрирования [a, b] на четное
число n равных частей с шагом h. На каждом отрезке [x0, x2],
[x2, x4], |
…, [xi 1, xi 1], |
…, [xn 2, xn ] подынтегральную |
|
функцию |
f(x) заменим |
интерполяционным |
многочленом |
второй степени: |
|
|
|
|
f(x) i (x) aix2 |
bix ci , xi 1 x xi 1. |
|
Таким образом, площадь элементарной |
трапеции с |
||
основанием 2h заменяется площадью фигуры, расположенной
под параболой, |
проходящей через точки Mi 1, Mi |
и Mi 1 |
||||
(рис. 9). Здесь |
сама функция |
f(x) |
изображена пунктирной |
|||
линией, а параболы, проходящие через точки M0 , M1, M2 и |
||||||
M2 , M3, M4 , выделены жирно. |
|
|
|
|||
Формула |
Симпсона |
(или |
формула |
парабол) |
||
записывается следующим образом: |
|
|
||||
b |
|
h |
y0 4 y1 y3 |
... yn 1 |
|
|
f(x)dx |
|
|||||
|
|
|||||
a |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 y2 y4 ... yn 2 yn .
57
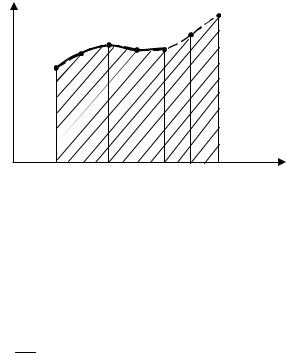
y=f(x) Mn
y
M1 M2 M3 M4
M0
a=x0 |
x2 |
x4 … xn=b |
x |
|
|
Рис. 9. Графическая иллюстрация метода Симпсона |
|
||||
|
|
|
1 |
dx |
|
Пример. Вычислить определенный интеграл I |
|
|
|||
1 x |
2 |
||||
|
|
|
0 |
|
|
с помощью метода Симпсона.
Подставим в формулу Симпсона значения функции, найденные в табл. 9:
I5 0.1 1 4 0.990099 ... 0.552486 3
2 0.961538 ... 0.609756 0.5 0.785398.
Контрольные вопросы
1.В чем заключается геометрическая интерпретация определенного интеграла? На чем основаны численные методы вычисления интегралов?
2.Как найти значение определенного интеграла с помощью метода прямоугольников? Какие модификации имеет данный метод?
3.Как вычислить интеграл с помощью метода
трапеций?
4.На чем основан метод Симпсона определения интегралов?
58
Задания для самостоятельной работы
Вычислить определенный интеграл с помощью метода: а) центральных прямоугольников; б) трапеций; в) Симпсона:
4.1. 1x2dx, |
h 0.1. |
0 |
|
4.2. 1 3x2 4x dx, h 0.1. |
|
0 |
|
4.3. 2x3dx, |
h 0.2. |
0 |
|
59
5. МЕТОДЫ |
РЕШЕНИЯ |
ОБЫКНОВЕННЫХ |
|
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ |
|
||
5.1. Общие |
сведения |
об |
обыкновенных |
дифференциальных уравнениях |
|
|
|
Обыкновенным дифференциальным уравнением
называется уравнение, содержащее одну или несколько производных от искомой функции y(x). Такое уравнение может быть записано в виде
F(x,y,y ,...,y(n)) 0,
где x – независимая переменная.
Вряде случаев удается выразить старшую производную
вявном виде, т.е.
y(n) f(x,y,...,y(n 1)).
Наивысший порядок n входящей в уравнение производной называется порядком дифференциального уравнения.
Решением дифференциального уравнения называется всякая n раз дифференцируемая функция y (x), которая после ее подстановки в уравнение превращает его в тождество.
Общее решение обыкновенного дифференциального уравнения n-го порядка содержит n произвольных постоянных
C1, C2 , …, Cn :
y(x,C1,C2,...,Cn)
иявляется решением уравнения при любых значениях C1, C2 ,
…, Cn .
Частное решение дифференциального уравнения получается из общего, если произвольным постоянным придать определенные значения.
В геометрической интерпретации общее решение описывает бесконечное семейство интегральных кривых с параметром С, а частному решению соответствует одна кривая и этого семейства.
60
