
2024
.pdfОтдельным классом задач оптимизации выступают задачи линейного программирования, математические модели которых включают линейную целевую функцию и линейные ограничения.
В общем виде задача линейного программирования записывается следующим образом:
n
F cjxj max(min),
j 1
n
aijxj ( )bi, |
i 1,...,m, |
j 1 |
|
xj 0, |
j 1,...,n, |
где aij, bi, cj - заданные |
постоянные величины; xj - |
неизвестные параметры задачи, n – количество неизвестных x1,...,xn , m – количество ограничений задачи.
Совокупность чисел x1,...,xn , удовлетворяющих ограничениям задачи оптимизации, называется допустимым решением (или планом).
План x1*,...,x*n , при котором целевая функция принимает свое максимальное (минимальное) значение,
называется оптимальным.
2.2. Основные |
модели |
задач |
линейного |
программирования |
|
|
|
Одной из возможных областей применения задач линейного программирования является оптимизация различных структурных и динамических характеристик технических и экономических систем. К наиболее используемым классам задач линейной оптимизации относятся:
1. Задача об оптимальном распределении ресурсов при выпуске продукции.
121
Пусть предприятие выпускает n видов изделий. Для их производства требуется m различных видов ресурсов. На производство каждого j-го вида изделия необходимо потратить aij единиц i-го ресурса, i 1,...,m, j 1,...,n . Ограничения по
каждому виду ресурсов составляют bi . Прибыль от продажи единицы изделия j-го вида составляет cj . Требуется составить
такой план производства продукции, при реализации которого будет получена максимальная прибыль.
Математическая модель задачи выглядит следующим образом:
n
F cjxj max,
j 1
n
aijxj bi, |
i 1,...,m, |
j 1 |
|
xj 0, j 1,...,n,
где xj - количество выпускаемых единиц j-го изделия, которое
необходимо определить.
2. Задача об оптимальном рационе.
Из n исходных материалов, закупаемых по цене cj , j 1,...,n , составляется m смесей для оптимального рациона. Каждый i-й вид смеси должен содержать в своем составе m компонентов в количествах, не меньших bi , i 1,...,m.
Известно, что в единице j-го материала содержится aij единиц
i-го компонента. Необходимо составить рацион, обеспечивающий заданный рацион питания и обладающий наименьшей стоимостью. Математическая модель задачи записывается в следующем виде:
122
n
F cjxj min,
j 1
n
aijxj bi, |
i 1,...,m, |
j 1 |
|
xj 0, j 1,...,n,
где xj - искомое количество единиц материала j-го вида,
которое необходимо приобрести для приготовления рациона. 3. Транспортная задача.
В m пунктах отправления хранятся запасы груза в количестве ai , i 1,...,m. Его необходимо доставить в n
пунктов назначения с потребностями bj , j 1,...,n . Стоимость перевозки груза из i-го пункта отправления в j-й пункт назначения составляет cij . Необходимо составить план
перевозок груза таким образом, чтобы стоимость перевозок была минимальной. Математическая модель задачи записывается следующим образом:
m n
Fcijxij min,
i1 j 1
m |
|
|
|
|
xij |
ai, |
j 1,...,n, |
||
i 1 |
|
|
|
|
n |
|
|
|
|
xij |
bj, |
i 1,...,m, |
||
j 1 |
|
|
|
|
xij 0, |
i 1,...,m, |
j 1,...,n, |
||
где xij - количество груза, которое необходимо перевезти из i-
го пункта отправления в j-й пункт назначения.
4. Задача об оптимальном раскрое материалов.
На производство поступают заготовки материала стандартного размера. Каждая заготовка может быть раскроена n способами для получения изделий m видов.
123
Известно, что при j-м варианте раскроя материала, j 1,...,n ,
изготавливается aij изделий i-го вида, i 1,...,m, а величина отходов составляет cj . План производства изделий i-го вида составляет bi . Необходимо раскроить заготовки материала таким образом, чтобы было получено необходимое количество изделий и величина отходов была минимальной. Математическая модель задачи выглядит следующим образом:
n
F cjxj min,
j 1
n
aijxj bi, i 1,...,m,
j 1
xj 0, j 1,...,n,
где xj - количество заготовок, раскраиваемых j-м способом.
5. Задача об оптимальной загрузке оборудования.
Пусть предприятию за время T необходимо выпустить n видов изделий в количестве bj , j 1,...,n . Продукция изготавливается на m станках, для каждого из которых известна производительность aij , т.е. число единиц продукции j-го вида, которое можно изготовить на i-м станке за единицу времени, и затраты cij на изготовление j-й продукции на i-м
станке. Необходимо составить оптимальный план работы оборудования, обеспечивающий наименьшие затраты. Математическая модель задачи записывается следующим образом:
124
m n
Fcijxij min,
i1 j 1
n
xij T, |
i 1,...,m, |
j 1 |
|
m |
|
|
|
aijxij bj, |
j 1,...,n, |
||
i 1 |
|
|
|
xij 0, |
i 1,...,m, |
j 1,...,n, |
|
где xij - время, затрачиваемое i-м станком на производство j-й
продукции
2.3.Общие принципы решения задач оптимизации
вMathcad
Для поиска локальных экстремумов в Mathcad есть две встроенные функции:
1) Minimize(f, x1, …, xn ) – возвращает значения неизвестных x1, …, xn , при которых целевая функция f достигает минимума;
2) Maximize(f, x1, …, xn ) – возвращает значения неизвестных x1, …, xn , при которых целевая функция f достигает максимума.
Перед вызовом функций Minimize() и Maximize() для неизвестных x1, …, xn необходимо задать начальное приближение.
Пример решения безусловной задачи оптимизации приведен на рис. 44.
125
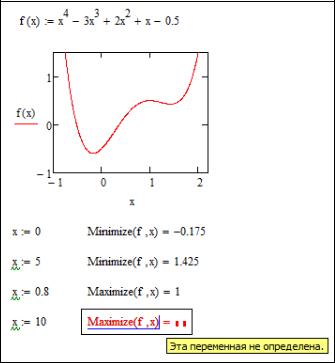
Рис. 44. Примеры решения безусловных задач оптимизации
Как видно из примера, на получаемый результат существенное влияние оказывает выбор начального приближения. Если оно выбрано удачно, то решение сходится к ближайшему максимуму (минимуму) функции, а вот если выбрать приближение вдали от экстремума, где f(x) неограниченно возрастает, то функция Maximize() выдает сообщение об ошибке, т.к. начальное приближение x 10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f(x), т.е. расходится при x .
В задачах на условный экстремум встроенные функции минимизации и максимизации должны быть включены в
126

вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства или уравнения), задающие ограничения на значения аргументов функции.
Примеры поиска условного экстремума на различных интервалах приведены на рис. 45.
Рис. 45. Примеры поиска условного экстремума
Если ограничить значения x интервалом, расположенным в окрестности правого локального минимума. то он будет без труда найден. В случае поиска максимума надо помнить об одной особенности – если на границе интервала целевая функция f(x) достигает большего значения, чем на локальном максимуме внутри интервала, то в качестве
127
решения, скорее всего, будет выдана граница интервала, хотя никакого экстремума там нет.
2.4. Решение задач линейного программирования в
Mathcad
Рассмотрим пример решения следующей задачи линейного программирования.
Пусть для производства двух видов изделий A и B предприятие использует три вида сырья. Нормы расхода сырья каждого вида приведены в табл. 23. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.
Учитывая, что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий будет максимальной.
|
|
|
Таблица 23 |
|
|
|
|
|
|
|
Нормы расхода |
Общее |
|
|
|
сырья на одно |
|
||
Вид сырья |
количество |
|
||
изделие, кг |
|
|||
|
сырья, кг |
|
||
|
A |
B |
|
|
|
|
|
||
1 |
12 |
4 |
300 |
|
2 |
4 |
4 |
120 |
|
3 |
3 |
12 |
252 |
|
Прибыль от реализации |
30 |
40 |
|
|
одного изделия, тыс. руб. |
|
|
||
Составим математическую модель задачи. Предположим, что предприятие изготовит x изделий вида А и y изделий вида B. Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида,
128

переменные x и y должны удовлетворять следующей системе неравенств:
12x 4y 300,
4x 4y 120,
3x 12y 252.
Общая стоимость произведенной предприятием продукции составляет f 30x 40y .
По своему экономическому содержанию переменные x и y могут принимать только неотрицательные значения, т.е. x,y 0.
Решение данной задачи в Mathcad приведено на рис. 46.
Рис. 46. Решение задачи линейного программирования в Mathcad
Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида B, то оно получит максимальную прибыль, равную fmax 30 12 40 18 1080 тыс. руб.
129
3. ЛАБОРАТОРНОЕ ЗАДАНИЕ
Задание 1. Найти экстремумы для заданной в табл. 24 функции.
Таблица 24
Вариант |
Функция |
|
|||
1 |
f(x) (x 1)2(x 2) |
||||
2 |
f(x) 5sin(x) 3cos(x) |
||||
3 |
f(x) x2ex |
|
|||
4 |
f(x) x3arctg(x) |
||||
5 |
f(x) (2x3 |
5)4 |
|||
6 |
f(x) 2x2 x |
|
|||
7 |
f(x) sin |
3 |
x |
|
|
|
|
|
|
||
|
|
||||
|
|
|
3 |
||
8 |
f(x) ln(x2 5) |
||||
Задание 2. Для задач, номера которых указаны в табл. 25, составить математические модели и найти оптимальное решение с помощью Mathcad.
|
|
|
|
|
|
|
|
Таблица 25 |
||
|
|
|
|
|
|
|
|
|
|
|
Номера |
|
|
|
Варианты |
|
|
|
|
|
|
задач |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
|
1 |
+ |
|
+ |
|
+ |
|
+ |
|
|
|
2 |
|
+ |
|
+ |
|
+ |
|
|
+ |
|
3 |
+ |
+ |
|
+ |
|
|
+ |
|
+ |
|
4 |
+ |
|
+ |
+ |
+ |
+ |
|
|
+ |
|
5 |
|
+ |
+ |
|
+ |
+ |
+ |
|
|
|
130
