
2024
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 20 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Вариант |
Неопределенный интеграл |
Определенный |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интеграл |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
e |
ln(x)2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
|
|
x |
3 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
2x |
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2 3 |
|
|
|
5 dx |
|
x x 1dx |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
3cos(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
|
|
|
sin(x) dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
e |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
cos(ln(x)) dx |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
2 |
|
|
|
|
|
|||||||||||||||
4 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
sin(x) |
dx |
|
||||||||||||||
|
|
|
2 x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos(x) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
2 |
sin(2x) |
|
||||||||||||
5 |
|
|
(tg(x) ctg(x)) |
dx |
|
|
|
|
|
x |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 1 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ln(2) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
dx |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6 |
|
|
|
|
2 1 x |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
ex 1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
ln(2) |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos(5x)cos(x) dx |
|
|||||||||||||||||
|
(2tg(x) 3ctg(x)) |
dx |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|||||||||
8 |
|
|
sin(x) cos(x) dx |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
111
Таблица 21
|
|
Методы интегрирования |
|
||
Варианты |
|
|
|
|
|
Метод левых прямоугольников |
Метод правых прямоугольников |
Метод средних прямоугольников |
Метод трапеций |
Метод Симпсона |
|
|
|
|
|
|
|
1 |
+ |
+ |
|
+ |
|
2 |
|
+ |
+ |
+ |
|
3 |
+ |
|
+ |
+ |
|
4 |
+ |
+ |
|
|
+ |
|
|
|
|
|
|
5 |
|
+ |
+ |
|
+ |
|
|
|
|
|
|
6 |
+ |
|
+ |
|
+ |
|
|
|
|
|
|
7 |
+ |
+ |
|
|
+ |
|
|
|
|
|
|
8 |
+ |
|
+ |
+ |
|
4.УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ОТЧЕТА
Отчет должен содержать:
- наименование и цель работы; - краткие теоретические сведения;
- задание на лабораторную работу; - результаты выполнения лабораторной работы.
5.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Как с помощью Mathcad найти аналитическое решение неопределенного интеграла?
2.Как с помощью Mathcad вычислить определенный интеграл?
112
Лабораторная работа № 6 ДИФФЕРЕНЦИРОВАНИЕ В MATHCAD
1.ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
1.1.Цель работы
Изучение основных методов дифференцирования функций в среде Mathcad; получение практических навыков реализации численных алгоритмов решения задачи Коши.
1.2.Используемое оборудование и программное обеспечение
Для выполнения лабораторной работы требуется ПЭВМ типа IBM PC с установленной ОС Windows XP и выше, математический пакет Mathcad 14 и выше.
2.МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
2.1. Дифференцирование в Mathcad
Операция дифференцирования реализована в Mathcad как в численной, так и в аналитической форме и обозначается при помощи специального оператора.
Для того чтобы аналитически найти производную
функции, надо нажать пиктограмму 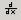 на панели инструментов Математический анализ, задать функцию и переменную дифференцирования, а затем ввести оператор символьного вычисления
на панели инструментов Математический анализ, задать функцию и переменную дифференцирования, а затем ввести оператор символьного вычисления 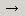 с панели Вычисления.
с панели Вычисления.
Для получения численного значения необходимо предварительно указать точку, в которой надо найти значение производной функции.
Примеры вычисления производной в среде Mathcad приведены на рис. 40.
113
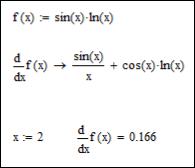
Рис. 40. Пример вычисления производной функции
2.2. Решение задачи Коши средствами Mathcad
Для решения обыкновенных дифференциальных уравнений в Mathcad есть следующие встроенные средства:
1) вычислительный блок Given/Odesolve - записывается следующим образом:
-ключевое слово Given;
-дифференциальное уравнение и начальные (или граничные) условия к нему;
-функция Odesolve(x, xk, n), где x - имя переменной, относительно которой решается уравнение, xk – конец интервала интегрирования (начало интервала интегрирования указывается в начальных условиях), n – необязательный параметр, определяющий число шагов интегрирования, на которых вычисляется решение дифференциального уравнения;
вкачестве ответа возвращается функция, являющаяся решением дифференциального уравнения.
Пример решения задачи Коши с помощью блока
Given/Odesolve приведен на рис. 41.
114
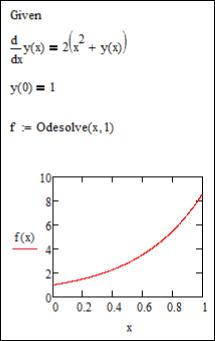
Рис. 41. Пример решение задачи Коши с помощью вычислительного блока Given/Odesolve
2) функция rkfixed(x0, x1, xk, k, D) решает дифференциальное уравнение или систему из n уравнений методом Рунге-Кутта четвертого порядка с фиксированным шагом; x0 – вектор начальных условий в точке x1, [x1,xk] - интервал интегрирования, k – количество промежутков, на которые разбивается интервал [x1,xk], D – векторная функция двух аргументов – скалярного x и векторного y, при этом y – искомая векторная функция аргумента x; функция возвращает матрицу размером (k 1) (n 1) . Функция, указываемая в параметре D, должна быть приведена к виду y F(x,y).
115
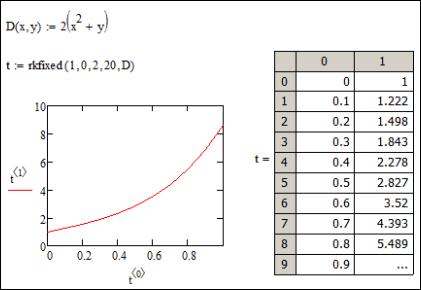
Пример решения уравнения с помощью функции rkfixed() приведен на рис. 42.
Рис. 42. Пример решения задачи Коши с помощью функции rkfixed()
3) функция Rkadapt(x0, x1, x2, k, D) решает дифференциальное уравнение или их систему методом РунгеКутта четвертого порядка с автоматическим выбором шага; параметры имеют тот же смысл, что у функции rkfixed(); функция возвращает матрицу размером (k 1) (n 1) . Пример решения уравнения с помощью функции rkfixed() приведен на рис. 43.
В большинстве случаев для решения дифференциального уравнения достаточно использовать функцию rkfixed(), однако если по различным причинам точность полученного решения неудовлетворительна или становится критичным время решения, можно использовать функцию Rkadapt(), поскольку она разбивает интервал не на равномерные шаги, а более оптимальным способом. Там где
116
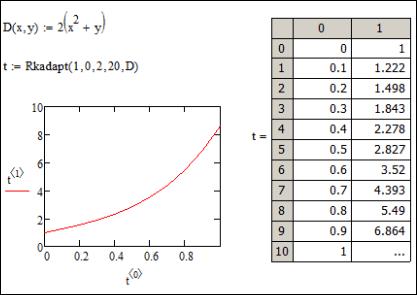
решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений – частыми. В результате для достижения одинаковой точности требуется меньшее число шагов, чем для rkfixed().
Рис. 43. Пример решения задачи Коши с помощью функции
Rkadapt()
3. ЛАБОРАТОРНОЕ ЗАДАНИЕ
Задание 1. Для заданной в табл. 22 функции найти производную в аналитическом и численном виде (в точке x 1).
Задание 2. С помощью встроенных средств Mathcad найти решение задачи Коши (табл. 22).
Задание 3. На встроенном языке программирования написать функции, реализующие численные алгоритмы решения задачи Коши (метод Эйлера и метод Рунге-Кутта).
Задание 4. Сравнить методы решения задачи Коши по времени решения.
117

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 22 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вариант |
Функция |
|
|
|
|
|
|
|
Задача Коши |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
f(x) ctg(x) x |
y cos(x 2y) cos(x 2y), |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
y(0) /4 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
yln3(y) y |
|
|
|
|
0 , |
|
||||||||||||||
|
f(x) 5sin(x) 3cos(x) |
|
|
|
x 1 |
|||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
e |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cox(2x) |
|
y 0, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
f(x) x2ex |
|
|
|
|
|
|
1 sin(y) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
f(x) x3arctg(x) |
y |
|
|
1 x |
2 |
|
y arcsin(x), |
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(0) 0 |
|
|
|
|
||||||||||
5 |
f(x) (2x3 |
5)4 |
y 3ytg(3x) sin(6x), |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
y(0) 1/3 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6 |
f(x) 2x2 x |
|
y |
|
|
3x2y |
|
y |
2 |
(x |
3 |
1), |
|
|||||||||||||||
|
|
x3 |
1 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(0) 1 |
|
|
|
|
||||||||||
7 |
f(x) sin |
3 |
x |
|
y 2ytg(x) y2 sin2(x) 0, |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y(0) 1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
y |
|
|
|
|
xln(x), |
|
|||||||||||
8 |
f(x) ln(x2 5) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
xln(x) |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y(e) e2 /2 |
|
|
|
|
|||||||||||
118
4.УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ОТЧЕТА
Отчет должен содержать:
- наименование и цель работы; - краткие теоретические сведения;
- задание на лабораторную работу; - результаты выполнения лабораторной работы.
5.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Как с помощью Mathcad выполнить аналитическое и символьное дифференцирование функции?
2.Как найти решение задачи Коши с помощью вычислительного блока Given/Odesolve?
3.Какие функции Mathcad предназначены для решения обыкновенных дифференциальных уравнений?
119
Лабораторная работа № 7 РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В MATHCAD
1.ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
1.1.Цель работы
Изучение основных принципов поиска экстремальных значений функции одной или нескольких переменных в среде Mathcad; получение практических навыков решения задач линейной оптимизации.
1.2.Используемое оборудование и программное обеспечение
Для выполнения лабораторной работы требуется ПЭВМ типа IBM PC с установленной ОС Windows XP и выше, математический пакет Mathcad 14 и выше.
2.МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
2.1. Основные понятия теории оптимизации
Оптимизация – это процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т.п.
Критерий, по которому оцениваются различные альтернативные варианты в задачах оптимизации, называется целевой функцией. В зависимости от контекста решаемой задачи для целевой функции необходимо найти либо максимальное, либо минимальное значение.
Если задача оптимизации имеет только целевую функцию, то она называется безусловной, если же на переменные задачи накладываются какие-либо ограничения, то задача называется условной.
120
