
1785
.pdf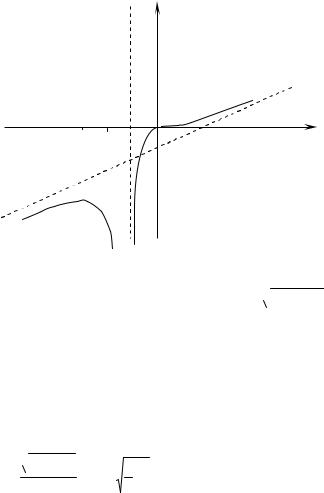
|
|
|
|
|
|
|
Таблица 1 |
||
x |
(- ,-3) |
-3 |
(-3,-1) |
-1 |
(-1,0) |
0 |
(0,∞) |
|
|
|
|
+ |
0 |
|
Не сущ. |
+ |
0 |
+ |
|
|
f (x) |
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
Не сущ. |
|
0 |
+ |
|
|
|
|
|||||||
f(x) |
Возр., |
Max |
убыв., |
Не сущ. |
возр., |
Точка |
Возр., |
|
|
|
|
вып. |
y= |
вып. |
|
вып. |
перег. |
вогн. |
|
|
|
|
-27/4 |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
-3 |
-1 0 |
x
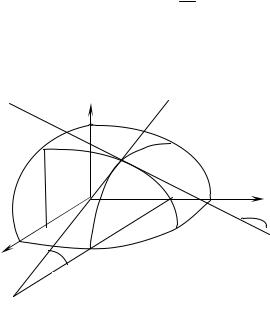
Рис. 19
Пример 4.6.3. Исследовать функцию y 3
 2x2 x3 и построить график.
2x2 x3 и построить график.
Решение:
1.Функция всюду определена: x R.
2.Не обладает свойством четности и нечетности.
3.Точки пересечения с осями
x2(2 x) 0; |
x 0, |
x 2; (0,0), (2,0). |
4. Вертикальных асимптот нет. Ищем наклонные: k lim 3
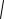 2x2 x3 lim 3 2 1 1,
2x2 x3 lim 3 2 1 1,
x |
x |
x x |
80

|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2x2 x3 x3 |
|||||||
|
|
|
|
2 |
3 |
|
|
|
|
|
||||||||||||
b lim |
|
2x |
|
x |
x |
lim |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
x |
|
|
|
|
|
x 3 2x2 x3 2 |
x3 |
2x2 x3 |
x2 |
|||||||||||||
lim |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
|
1 |
4x4 4x5 x6 3 |
2 |
3 |
|
|
|
|
|||||||||||||
3 |
|
1 1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
|
|
|
|
||||||||||||||||
|
|
|
x6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Функция имеет наклонную асимптоту у= х+2/3. 5. Ищем критические точки первого рода.
|
|
|
y |
|
4x 3x2 |
|
|
|
|
|
4 3x |
|
x1 0,x2 2,x3 4/3. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 x4(2 x)2 |
3 3 x(2 x)2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
6. Ищем критические точки второго рода. |
||||||||||||||||||||||
|
|
|
33 |
|
(4 3x) |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
x(2 x)2 |
|
|
|
|
|
|
|
[(2 x)2 x2(2 x)] |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y |
1 |
|
|
|
|
|
|
3 |
3 |
x |
2 |
(2 x) |
4 |
|
= |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
33 x2(2 x)4
93
 x3(2 x)6 (4 3x)(2 x)[2 x 2x] 9x(2 x) (4 3x)(2 3x)
x3(2 x)6 (4 3x)(2 x)[2 x 2x] 9x(2 x) (4 3x)(2 3x)
93 x4(2 x)8 93 x4(2 x)5
|
18x 9x2 |
8 12x 6x 9x2 |
|
8 |
, x 0,x 2. |
|||
|
|
|
|
|||||
|
93 x4(2 x)5 |
93 x4(2 x)5 |
1 |
2 |
||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
х |
( ;0) |
0 |
(0;4/3) |
4/3 |
|
(4/3; |
2 |
|
(2; ) |
||||
|
|
|
|
|
|
|
|
2) |
|
|
|
||
y |
|
н.с. |
+ |
0 |
|
|
|
|
|
|
н.с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
н.с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
max |
|
|
|
|
|
т.п. |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
у=0 |
|
|
|
|
|
|
y |
2 |
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
|
|
|
|
|
|
|
|
|

7. На основании вышеизложенного строим график.
y
|
4/3 |
2 |
x |
|
0 |
||||
|
Рис. 20
Вопросы для самопроверки
1.Сформулируйте необходимое и достаточное условие возрастания (убывания) функции на промежутке.
2.Дайте определение точки максимума функции.
3.Какие точки являются критическими точками первого
рода?
4.В чем различие между минимумом и наименьшем значением функции?
5.Какой график функции называется выпуклым?
6.Как находятся интервалы выпуклости и вогнутости графика функции?
7.Что называется критическими точками второго рода?
8.Как определяется асимптота графика функции? Когда появляются вертикальные и наклонные асимптоты?
9.Изложите общую схему исследования функции и построения ее графика.
82

Задачи для самостоятельного решения
1. Найти промежутки возрастания и убывания функции y 
 x2 2x .
x2 2x .
|
Ответ: функция возрастает при x (0, ), функция убы- |
|||||||||||||
вает при x (- ,-2). |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Найти экстремумы функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
y = x3 -9x2 +15x. Ответ: ymax y 1 7, |
ymin |
y 5 25. |
|||||||||||
|
y cos x sin x при x (0,π). Ответ: ymax |
|
|
|
|
|
|
|||||||
|
|
|||||||||||||
3. |
y |
|
2. |
|||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|||||
|
1 |
|
1 |
|
|
|
|
|
|
|||||
4. |
y x 1 ln x 1 . Ответ: ymin y |
|
1 |
|
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
e |
|
|
|
e |
|
|
|
|
|
||||
5. |
Найти асимптоту графика функции y |
|
|
1 |
|
|
|
. |
||||||
x2 |
2x 2 |
|||||||||||||
Ответ: y 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
6. |
Найти асимптоты графика функции y e |
x 1 |
-1. |
|||||||||||
Ответ: y 0 , x 1 0 .
5. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
5.1. Понятие функции двух переменных
Говорят, что определена функция z = f (x,y) двух переменных х,у , если каждой паре значений независимых переменных (аргументов) х,у из области D по некоторому закону f ставится в соответствие определенное значение переменной z из множества Z. Область D называется областью определения функции z, а множество Z - множеством значений функции. Поскольку каждой паре чисел х,у на плоскости Оху можно поставить в соответствие точку М (х,у), то функцию двух перемен-
83

ных рассматривают как функцию точки М z f M из некоторой области D плоскости Оху .
Точка называется внутренней точкой множества D, ес-
ли у этой точки есть окрестность, состоящая из точек данного множества. Точка называется граничной точкой множества D, если любая окрестность этой точки содержит как точки принадлежащие множеству D, так и точки ему не принадлежащие. Совокупность всех граничных точек множества D называется его границей. Множество D называется замкнутым
D, если оно содержит все свои граничные точки. Множество D называется открытым, если все его точки являются внутренними.
Множество D точек плоскости Оху называется областью, если: во-первых, множество D является открытым, т.е. состоит только из внутренних точек, во-вторых, множество D является односвязным, т. е. любые две внутренние точки множества должны соединяться непрерывной линией, целиком принадлежащей области.
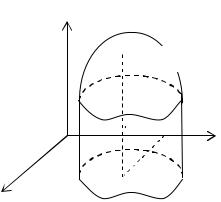
Функция двух переменных имеет простую геометрическую интерпретацию. Возьмем пространственную декартову систему координат. Для произвольной точки М (х,у) в области D вычислим соответствующее значение функции z = f (х,у). Множество точек P(x,y,z) образует некоторую поверхность с уравнением z = f(х,у). Таким образом, геометрической интерпретацией функции двух переменных является поверхность (рис. 21.), аппликата каждой точки которой вычисляется по
закону z =f(х,у). Например, для функции z |
1 x2 y2 гео- |
метрическим образом является верхняя полусфера. Область определения данной функции определяется неравенством
1 x2 y2 0 или x2 y2 1.
84
Z= f (x,y)
z
P (x1,y1,z1)
y
y
x
 M
M
x
Рис. 21
Существует еще один способ изображения функции двух переменных, основанный на построении сечений поверхности z = f (х,у) плоскостями z c, где с - любое число. Линией уровня называется множество точек плоскости Оху, в которых функция принимает одно и то же значение с. Множество линий уровня дает представление о поверхности подобно тому, как в картографии линии уровня описывают рельеф местности. Все сказанное об определении функции двух переменных легко распространяется на случай функции большего числа переменных. Геометрическая интерпретация функции в этом случае отсутствует.
5.2. Частные производные и частные дифференциалы первого порядка
Пусть функция z =f (х, у) определена и непрерывна в точке М0(х0, у0) и ее некоторой окрестности. Зафиксируем значение у = у0, а переменная х пусть испытает приращение х. При этом переместимся из точки M0 x0,y0 в точку M1 x0 x,y0 .
Получим функцию одной переменной z =f (х, у0). Разность
xz f x0 x,y0 f x0,y0
называется частным приращением функции z по переменной х.
85

Частной производной функции z по переменной х в точке
М0 (х0, у0) называется предел отношения xz при х 0
x
z |
= f |
(x |
0 |
, y |
0 |
) = lim |
xz |
= lim |
f (x0 x, y0) f (x0,y0) |
. |
x x |
|
|
x 0 x |
x 0 |
x |
|||||
В определении частной производной не все координаты равноправны: переменная у фиксирована, а х изменяется.
При перемещении из точки М0(х0,у0) в точку М2(х0,у0+ у) получим частное приращение функции z по переменной y
yz f x0,y0 y f x0, y0 .
|
|
Частной производной функции z по переменной y |
в |
|
|||||||||||||||
точке М0 (х0, у0) называется предел отношения |
yz |
при y 0 |
|||||||||||||||||
y |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
= |
z |
= f (x ,y )= lim |
y z |
= lim |
|
f (x ,y y) f (x ,y |
) |
|
. |
|||||||||
|
|
0 0 |
|
0 |
0 |
|
|
||||||||||||
y |
|
y |
y |
0 0 |
y 0 y |
|
y 0 |
|
|
y |
|
|
|
|
|
||||
|
|
Частные производные |
|
z |
и |
|
z |
характеризуют мгновен- |
|||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
||||
ную скорость изменения функции z в точке М0 (х0, у0) в направлении координатных осей Ох и Оу.
При вычислении частных производных остаются в силе правила дифференцирования функции одной переменной, а также таблица производных, если другие аргументы считаются
постоянными величинами. |
|
|
|
|
|
|
|||||
Пример 5.2.1. Найти частные производные |
функции |
||||||||||
z x3 9x2 y y4 .Решение: |
|
z |
=3x2 18xy, |
z |
= |
9x2 4y3 . |
|||||
|
|
|
|||||||||
|
|
|
|
|
|
x |
y |
|
|||
Здесь при нахождении |
z |
|
переменная y считается констан- |
||||||||
x |
|||||||||||
|
z |
|
|
|
|
|
|
|
|||
той, при нахождении |
|
переменная x считается константой. |
|||||||||
y |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
86 |
|
|
|
|||
Пример 5.2.2. Найти частные производные функции z ln(x2 y y3) .
Решение: |
z |
|
2xy |
, |
z |
|
x2 3y2 |
. |
|
x |
x2 y y3 |
y |
x2 y y3 |
||||||
|
|
|
|
|
Рассмотрим геометрический смысл частных производных функции двух переменных. Пусть уравнение z =f(х, у) есть уравнение поверхности, изображенной на рис. 22.
Проведем плоскость х= х0. В сечении этой плоскостью поверхности получается линия L2. При данном х0 рассмотрим на плоскости точку М0. На поверхности ей соответствует точка
Р. Частная производная |
|
z |
|
равна тангенсу угла, образованно- |
||
|
y |
|||||
|
|
|
|
|
||
го касательной к кривой L2 |
в точке М с положительным на- |
|||||
правлением оси Оу: |
z |
|
M0 |
tg . Для уточнения стоит отме- |
||
|
||||||
y |
|
|
||||
|
|
|
|
|||
тить, что касательная лежит в плоскости х= х0.
По аналогии частная производная z численно равна тан-
x
генсу угла наклона касательной к линии L1 , представляющей
сечение |
поверхности |
z f x, y |
|
|
плоскостью |
у=у0, |
|||||||||||||||||||
т.е. |
z |
|
M0 |
tg . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
M0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 22
87

5.3. Полное приращение функции и полный дифференциал
Пусть функция двух переменных f(x,у) определена и непрерывна в точке М0(х0 ,у0) и ее окрестности. Если переменные x и y изменились, приняв значения x x0 x и у=у0+ у, то
функция f(x,у) испытала полное приращение z=f(М) - f(М0) = =f(x0+ x, у0+ у) - f(x0, у0), соответствующее перемещению из точки М0(х0 ,у0) в точку М(х ,у).
Функция z=f(x,у) называется дифференцируемой в точке М0 (х0,у0), если полное приращение функции представимо в виде: z=А x+В y+ x y , где А и В не зависят от x иy , а выражение x y является бесконечно малой величиной более высокого порядка малости по сравнению с x и
y .
Линейная по x и y часть полного приращения функ-
ции f (x, у) называется полным дифференциалом функции f(x,у)
в точке М0 (х0,у0) и обозначается dz: dz=А x+В y.
Следует отметить, что полное приращение функции f(x,у) можно записать z=dz+ x y .
Необходимое условие дифференцируемости сформулировано в виде теоремы.
Теорема. Если функция z=f(x,у) дифференцируема в точке М0(х0,у0), то эта функция имеет в точке М0 частные производные, причем
fx(x0, y0 ) =А, fy(x0, y0)=В.
Следовательно, полный дифференциал можно записать в виде:
dz= z x+ z y.
x y
Поскольку x=dх и y=dу, то
88

dz= fx(x, y)dx+ fy (x, y)d.y
Слагаемые fx(x, y)dx=dxz и fy (x, y)dy=dyz называют-
ся частными дифференциалами соответственно по x и y .
Для функции нескольких переменных наличие частных производных не является достаточным условием дифференцируемости. Достаточные условия дифференцируемости функции нескольких переменных сформулированы в виде теоремы.
Теорема. Если функция z=f(x,у) имеет частные производные в точке М0 (х0,у0) и некоторой ее окрестности, и эти частные производные являются непрерывными функциями, то функция дифференцируема в точке М0 , причем
dz= fx (x0 , y0 ) х+ fy (x0 , y0 ) у.
Теорема. Если функция f(x,у) дифференцируема в точке М0, то она непрерывна в этой точке.
5.4. Производная по направлению. Градиент
Для описания скорости изменения функции u=f(x,у,z) в
точке M x, y,z |
по |
направлению, задаваемому вектором |
||
l cos ,cos ,cos , |
введем |
понятие производной по на- |
||
правлению. Проведем из точки |
M x, y,z |
прямую L, парал- |
||
лельную вектору |
l . |
Выберем |
на прямой |
L вторую точку |
M1 x x, y y,z z , отстоящую от точки M на расстоя-
нии l |
x 2 |
y 2 z 2 . При переходе от точки M к |
||||||
точке M1 |
функция u=f(x,у,z) испытывает приращение |
|||||||
|
|
u f x x, y y,z z f x, y,z . |
||||||
Производной функции u=f(x,у,z) в точке M по направле- |
||||||||
|
|
|
|
|
|
|
|
|
нию вектора l |
называется предел отношения |
u |
при стрем- |
|||||
|
||||||||
|
|
|
|
|
|
l |
||
лении точки M1 |
|
|||||||
к точке M |
||||||||
|
|
|
|
89 |
|
|
|
|
