1785

Пример 2.6.3.

3. Если дробь является иррациональной, т.е. в числителе или знаменателе есть корни, то для раскрытия неопределенно-

0

сти вида необходимо выделять в качестве множителей

0

бесконечно малые величины, не содержащие радикалов, посредством умножения числителя и знаменателя на иррационально сопряженное выражение.

Пример 2.6.4.

При раскрытии неопределенности вида для представления бесконечно малых величин в удобном виде, не содержащем иррациональности, необходимо умножить и разделить на иррационально сопряженное выражение.

Пример 2.6.6.

20

требует приведения к общему знаменателю. В результате преобразований получим уже рассмотренный случай не-

2.7. Сравнение бесконечно малых величин

Бесконечно малые величины x и x называются

бесконечно малыми величинами одного порядка малости при

x a, если lim x C , где C является не равной нулю кон-

x a x

стантой.

Бесконечно малые величины x и x называются эк-

вивалентными бесконечно малыми величинами при x a, ес-

ли lim x 1. В качестве эквивалентных бесконечно малых

x a x

величин можно назвать величины x и sin x при x 0 .

21

Пример 2.7.1. Показать, что бесконечно малые величины

Бесконечно малая величина x является бесконечно малой величиной более высокого порядка малости по сравнению с бесконечно малой величиной x , если

lim x 0.

x a x

При вычислении пределов бесконечно малые величины могут заменяться эквивалентными.

10. a0 xn a1xn 1 an x~ a0 xn a0 0 .

22

Пример 2.7.3.

2.8. Непрерывность функции в точке

Пусть функция y f x определена на некотором интервале a,b . Возьмем произвольную точку x0 a,b . Для любо-

ся приращением функции f(x) в точке x0 и обозначается y

или f .

y

y f x

f x0 x

y

f x0

Функция y f x , определенная в точке x0 и ее окрест-

ности, называется непрерывной в точке x0 , если бесконечно

малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.

lim y 0.

x 0

Можно дать второе определение непрерывности функции, следующее из первого. Для этого рассмотрим детальнее предыдущее определение

Функция y f x , определенная в точке x0 и в некото-

рой ее окрестности, называется непрерывной в точке x0 , если

существует предел функции в этой точке, который равен значению функции точке x0. Это означает, что при нахождении предела непрерывной функции достаточно в выражение функции f x подставить вместо аргумента x его значение x0 .

Третье определение непрерывности функции в точке связано с понятием одностороннего предела. Предел функции y f x называется левосторонним, если при x a аргумент x остается все время меньше a, что обозначается таким обра-

ется правосторонним, если при x a аргумент x остается все время больше a. Правосторонний предел записывается так:

lim f x или lim f x .

x a x a 0

Функция y f x , определенная в точке a и ее окрестности, называется непрерывной в точке a, если предел функ-

24

ции y f x справа при x a равен пределу функции слева и равен значению функции y f x в самой точке a:

Если функция y f x непрерывна в каждой точке неко-

торого интервала a;b , то говорят, что функция непрерывна на этом интервале.

2.9. Точки разрыва функции и их классификация

Если в точке a не выполняется хотя бы одно из условий третьего определения непрерывности функции y f x , то точка a является точкой разрыва. Существует три типа точек разрыва: точка устранимого разрыва, точка разрыва первого рода или скачок, точка разрыва второго рода.

Точка устранимого разрыва образуется, если функция y f x определена в окрестности точки a, но не в самой точке, а пределы функции слева и справа должны быть одинаковы, т.е.

Если в точке aсуществуют конечные неравные пределы функции слева и справа (односторонние пределы), т. е.

25

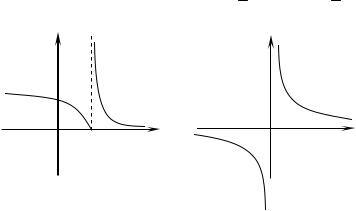
разрыва второго рода, поскольку lim 1 , lim 1 .

Рис. 6 Рис. 7

2.10. Основные теоремы о непрерывных функциях

Теоремы о непрерывности функций в точке a и ее окрестности следуют непосредственно из соответствующих теорем о пределах.

Теорема 1. Сумма двух функций, непрерывных в точке a и ее окрестности есть функция, непрерывная в точке a и ее окрестности.

Теорема 2. Произведение двух функций, непрерывных в точке a и ее окрестности, есть функция, непрерывная в точке a и ее окрестности.

Теорема 3. Частное от деления двух функций, непрерывных в точке a и ее окрестности есть функция, непрерывная в точке a и ее окрестности, если знаменатель в точке a не равен нулю.

Теорема 4. (Теорема о непрерывности сложной функции) Пусть y f x - сложная функция. Если функция

27

x непрерывна в точке a, а функция y f непрерывна

вточке a a , то сложная функция непрерывна в точке a.

2.11.Свойства функций, непрерывных на отрезке

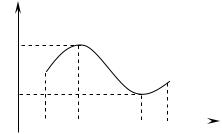
1.Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значения.

отрезке a;b , принимает наибольшее значение M в точке x1,

а наименьшее m- в точке x2 . Для любого x a;b имеет ме-

сто неравенство m f x M .

2.Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

3.Если функция y f x непрерывна на отрезке a;b , и

на его концах принимает значения разных знаков, то внутри отрезка a;b найдется хотя бы одна точка c, в которой данная функция y f x обращается в ноль: f c 0.

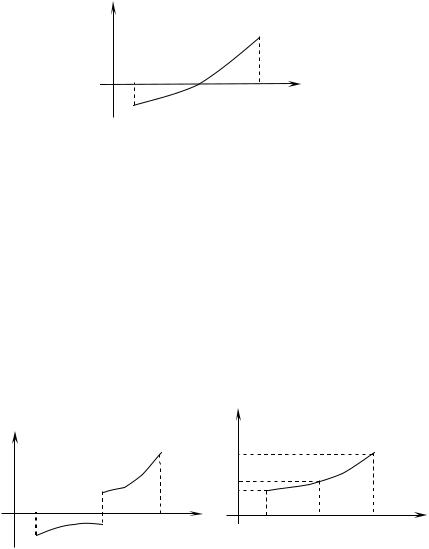
Геометрический смысл заключается в том, что если график непрерывной функции переходит с одной стороны оси Ox на другую, то он обязательно пересекает ось Ox (рис.9).

28

y

Рис. 9

В случае нарушения условия о непрерывности функции на отрезке вышеуказанная теорема может не выполняться

(рис. 10).

4. Если функция y f x непрерывна на отрезке a;b , и принимает на его концах неравные значения f a A и f b B , то на этом отрезке она принимает и все промежуточные значения между A и B .

Геометрическая интерпретация сводится к тому, что для любого числа C , заключенного между A и B , найдется такая внутренняя точка c, что f c C , т.е. прямая y C пересечет график функции y f x , по крайней мере, в одной точке

(рис. 11).

y

29