
1594
.pdfи представимые в виде произведения
u(x,t) X (x)T (t), |
(3.7) |
где X (x) функция только переменного x, T (t) функция только переменного t .
Подставив функцию u(x,t) вида (3.7) в уравнение (3.3), получим равенство
T t X x a2 T t X x .
Разделив его на a2TX , придём к соотношению
1 |
|
T t |
|
X x |
|
|
|
|
. |
||
a2 |
T t |
X x |
|||
Последнее равенство может выполняться для всех 0 x l , t 0 только то-
гда, когда оба отношения сохраняют постоянные и равные друг другу значения (являются равными константами). Обозначая такое общее постоянное значение через c , получаем равенства
1 |
|
T t |
c , |
X x |
c. |
(3.8) |
a2 |
T t |
X x |
В результате приходим к двум обыкновенным дифференциальным уравнениям для определения функций X (x) и T (t) :
X cX 0 , |
|
(3.9) |
|
T ca2T 0 . |
|
(3.10) |
|
Из граничных условий следует, что |
|
|
|
u(0,t) X 0 T t 0 , |
u(l,t) X l T t 0, |
t 0. |
(3.11) |
Из тождеств (3.11) получаем: |
|
|
|
X (0) X (l) 0, |
|
(3.12) |
|
81
так как иначе имели бы T (t) 0 u(x,t) 0.
Для уравнения (3.9) условия (3.12) не являются начальными, это так называемые краевые условия. Задача решения уравнения (3.9) при условиях (3.12)
называется краевой задачей.
Для уравнения (3.9) составим характеристическое уравнение:
k2 c 0.
Здесь возможны следующие случаи:
1)c 0 , т.е. c 2 , 0 ;
2)c 0;
3)c 0 , т.е. c 2 , 0.
Рассмотрим каждый из этих случаев.
1. c 2 , k , 0. Корни уравнения действительные и различные, и, следовательно, общее решение уравнения (3.9) имеет вид
X x C1e x C2e x .
Согласно краевым условиям будем иметь
C1 1 C2 1 0, |
|
|
|
|
|
|||
C e l C |
2 |
e l |
0. |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Поскольку определитель этой системы |
|
1 |
1 |
|
|
e l e l 2 sh l 0, |
||
|
|
|||||||
|
|
|
e l |
e l |
|
|
|
|
то она имеет единственное решение C1 0 , |
C2 |
0 . |
Полученный результат |
|||||
приводит к нулевому решению: |
|
|
|
|
|
|
|
|
Xx 0 u(x,t) 0.
2.c 0, k1 k2 0 . В этом случае общее решение уравнения (3.9) имеет
вид
X x C1 C2 x .
Для того чтобы функция X ( ходимо и достаточно, чтобы
x) удовлетворяла краевым условиям (3.12), необвыполнялась система условий
82

C1 C2 0 0,C1 C2 l 0.
Поскольку определитель этой системы l 0 , то она имеет единственное
решение C1 0, C2 |
0. Т.е. и в этом случае X (x) 0 u(x,t) 0. |
|
3. c 2 , |
k |
i . Корни характеристического уравнения чисто мни- |
|
1, 2 |
|
мые, поэтому общее решение уравнения (3.9) имеет вид
X x C1 cos x C2 sin x .
Согласно краевым условиям будем иметь
C1 C2 0 0,
C1 cos l C2 sin l 0.
Из этой системы получаем:
|
|
C1 0, C2 |
sin l 0 . |
|
|
|||||
Поскольку C2 0 |
(в противном случае опять X (x) 0 |
u(x,t) 0), при- |
||||||||
ходим к выводу, что необходимо потребовать, |
чтобы sin l обратился бы в |
|||||||||
нуль. Отсюда следует, что l m , m 1, 2, |
... ( m 0 , иначе опять полу- |
|||||||||
чаем нулевое решение). Таким образом, |
|
|
|
|||||||
|
|
|
|
m |
, |
m 1, 2, .... |
|
(3.13) |
||
|
|
|
|
|
||||||
|
|
m |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Этим значениям m будут соответствовать решения уравнения (3.9) вида |
||||||||||
X |
|
x A |
sin |
m x |
, A E1 , m 1, |
2, .... |
(3.14) |
|||
m |
|
|||||||||
|
m |
|
|
l |
m |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
Ясно, что в формуле (3.14) достаточно брать только положительные значения m , т.к. в полученных решениях множителями являются произвольные постоянные, а функция sin y нечётная. Поэтому везде далее будем рассмат-
ривать только натуральные m.
Постоянные m2 называются собственными числами, а функции sin ml x собственными функциями уравнения (3.9) с краевыми условиями
(3.12).
83
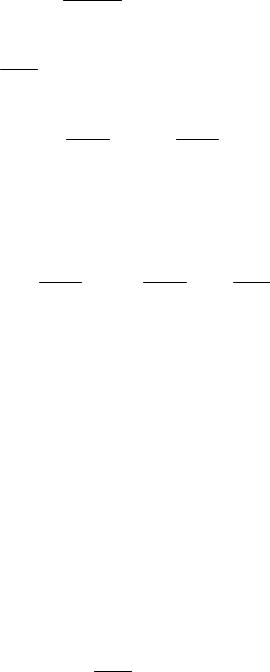
Переходим к решению уравнения (3.10), в котором |
c 2 |
, 2 |
|
m2 2 |
, |
||||
|
|||||||||
|
|
|
|
|
m |
m |
|
l2 |
|
т.е. |
|
|
|
|
|
|
|
|
|
|
|
m2 2a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
T |
t |
l2 T t 0 . |
|
|
|
|
|
||
|
|
|
|
|
|
||||
Запишем его характеристическое уравнение:
k2 m2 l22a2 0 .
Оно имеет корни k1, 2 i ml a , и потому общее решение рассматриваемого
уравнения имеет вид
Tm t Bm cos m l at Dm sin m l at ,
где Bm и Dm произвольные постоянные, m 1, 2,....
Окончательно решение um (x,t) Tm X m уравнения (3.3) для каждого m
можно записать в виде
um x,t am cos m l at bm sin m l at sin ml x ,
где am и bm новые произвольные постоянные, m 1, 2,.... Так как уравнение (3.3) линейное, то его решением будет и сумма всех решений um (x,t) , т.е.
функция |
|
m at |
|
m at |
m x |
|
|
||
|
|
|
|
||||||
u x,t am cos |
|
bm sin |
|
sin |
|
, |
(3.15) |
||
l |
l |
l |
|||||||
m 1 |
|
|
|
|
|
||||
в предположении, что ряд, определяющий функцию u(x,t) , можно дважды почленно дифференцировать по переменным x и t . Ясно, что функция u(x,t) удовлетворяет краевым условиям (3.5), так как им удовлетворяет каждая из функций um ( x, t) .
Для определения произвольных постоянных am , bm воспользуемся начальными условиями (3.4):
f x am sin ml x , 0 x l ,
m 1
84

F x bm ml a sin ml x , 0 x l .
m 1
Полученные формулы представляют собой разложения в ряд Фурье на от- |
||||||||
резке [0;l] по синусам функций f |
x и F x . Коэффициенты в этих разло- |
|||||||
жениях будут определяться по известным формулам |
||||||||
|
am |
2 l |
f x sin |
m x |
dx , |
|||
|
l 0 |
|
|
|||||
|
|
|
|
l |
||||
b |
m a |
2 l |
F x sin |
m x |
dx , |
|||
|
|
|||||||
m |
l |
l |
0 |
|
|
l |
||
|
|
|
||||||
m 1, 2,... .
Таким образом, решение уравнения (3.3) при начальных условиях (3.4) и граничных условиях (3.5) имеет следующий окончательный вид:
|
|
|
|
|
|
|
m at |
|
|
|
|
m at |
m x |
|
|
||||||
|
|
|
|
u x,t am cos |
|
|
|
bm sin |
|
|
sin |
|
, |
(3.16) |
|||||||
|
|
|
|
|
l |
|
|
l |
l |
||||||||||||
где |
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
2 l |
f x sin |
m x |
dx , b |
|
2 |
l |
F |
x sin |
m x |
dx , m 1, 2,.... |
|||||||||
m |
|
|
m a 0 |
|
|||||||||||||||||
|
l |
0 |
|
l |
m |
|
|
|
|
|
l |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Условия, которые надо наложить на функции f (x) и F(x) для того, чтобы
выполнялось предположение о возможности двукратного почленного дифференцирования ряда (3.15), можно найти в [3, с.100]. Обычно в физических задачах эти условия соблюдаются.
Метод, применённый для нахождения решения уравнения (3.3), удовлетворяющего начальным условиям (3.4) и краевым условиям (3.5), называется
методом Фурье или методом разделения переменных. Его подробное опи-
сание дано в [3, с.119].
3.5.Физический смысл решения уравнения колебаний ограниченной струны
Каждое из слагаемых полученного решения (3.16) представим в виде
85
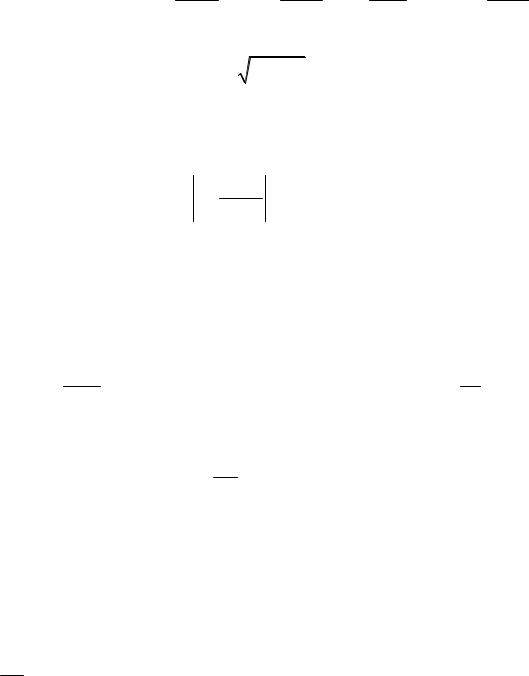
um x,t am cos m l at bm sin m l at sin ml x m cos m l at m
sin |
m x |
, где |
m |
|
a2 |
b2 |
, |
m |
arctg |
bm |
, m 1,2,.... |
|
|
||||||||||
|
l |
|
m |
m |
|
|
am |
|
|||
|
|
|
|
|
|
|
|
|
|||
Рассмотрим произвольную точку струны x x0 , отличную от граничных точек x 0 и x l . Выбранная точка будет совершать гармонические коле-
бания с амплитудой m sin m x0 . Такие колебания точек струны, описывае- l
мые функцией um ( x, t) , называют стоячей волной струны.
Выясним, какие точки остаются неподвижными в процессе колебаний. Все такие точки x являются решениями уравнения
sin m x 0 , l
так что ml x n , n 1,2,3, ... . Отсюда следует, что x nml , n 1,2,3,.., m 1.
Точки с найденными координатами в процессе колебаний остаются неподвижными для каждого значения n и называются узловыми.
Частота колебаний la , соответствующая слагаемому um ( x, t) с номе-
ром m 1, называется основной частотой колебаний. Остальные частоты кратны ей.
Основная частота определяет основной тон звуковых колебаний, все остальные частоты называются обертонами. В звучании участвует только конечное число частот. Тем самым каждая струна характеризуется своим тембром, т.е звучанием.
Энергия гармонических колебаний каждого слагаемого будет порядка m14 . Отсюда следует, что с ростом m влияние гармоник (членов ряда) стано-
вится всё меньше и меньше. Поэтому в акустике решение в виде бесконечного ряда заменяется конечной суммой стоячих волн. В общем случае решение уравнения колебаний ограниченной струны представляет собой бесконечную сумму стоячих волн с частотами, кратными основной частоте.
П р и м е р Найти решение уравнения колебаний струны
2u a2 2ut2 x2
86

с неподвижными концами
u(0,t) u( ,t) 0
при начальных условиях
u(x, 0) sin3 x,
u (x, 0) 0.
t
Решение данной задачи имеет вид
u(x,t) am cos mat bm sin mat sin mx ,
m 1
где
am 2 sin3 x sin mx dx , m 1, 2, ... ,
0
bm 2 0 sin mx dx 0, m 1, 2,... .
m a 0
Здесь am коэффициенты разложения функции sin3 x в ряд Фурье по синусам. Заметим, что sin3 x 34 sin x 14 sin 3x. Ясно, что правая часть этого равенства как раз и является рядом Фурье для sin3 x разложение в ряд Фу-
|
|
|
n |
|
|
рье по синусам любой функции вида ck sin k x совпадает с самой этой |
|||||
|
|
|
k 1 |
|
|
функцией. При этом a 3 , a |
1 , все же остальные коэффициенты a |
m |
|||
1 |
4 |
3 |
4 |
|
|
|
|
|
|
||
равны нулю. Поэтому искомое решение уравнения имеет вид |
|
||||
u(x,t) |
3 cos at sin x |
1 cos3at sin 3x. |
|
||
|
|
4 |
|
4 |
|
Ко н т р о л ь н ы е в о п р о с ы и з а д а н и я
1.Дайте определение дифференциального уравнения в частных производных. Какое число называется порядком такого уравнения? Дайте определение решения дифференциального уравнения в частных производных.
87
2.Приведите примеры простейших уравнений гиперболического, параболического и эллиптического типа.
3.Сформулируйте задачу о свободных колебаниях упругой ограниченной струны с закреплёнными концами. Приведите формулу, дающую решение такой задачи.
Заключение
В данном пособии не рассмотрены многие важные вопросы теории числовых и функциональных рядов. Так, в первом параграфе не были приведены некоторые тонкие и сложно доказываемые признаки сходимости положительных и знакопеременных числовых рядов, не рассматривались сочетательное и переместительное свойства рядов, которыми они существенно отличаются от конечных сумм, не вводилось понятие произведения рядов. В параграфе, посвящённом изучению функциональных рядов, не вводилось понятие равномерной сходимости таких рядов и в нем не рассматривались свойства равномерно сходящихся функциональных рядов. Последним отчасти объясняется то, что не были доказаны свойства 1 и 2 сумм степенных рядов. Не были рассмотрены многие важные свойства рядов Фурье и применение этих рядов к решению различных задач математической физики. Изложение упомянутых признаков, понятий и свойств привело бы к значительному увеличению объёма пособия и к введению сложного математического аппарата.
Студентам, желающим более глубоко изучить тему “Ряды”, авторы рекомендуют обратиться к изданиям [1], [2], [4], [5].
Библиографический список
1.Ильин, В.А. Высшая математика / В.А. Ильин, А.В. Куркина. М.: Про-
спект, 2008. 600 с.
2.Фихтенгольц, Г.М. Основы математического анализа: в 2 т. Т. 2 / Г.М. Фихтенгольц. М. : Наука, 2005. 464 с.
3.Тихонов, А.Н. Уравнения математической физики / А.Н. Тихонов, А.А. Самарский. М.: Изд-во МГУ, 1999. 799 с.
4.Толстов, Г.П. Ряды Фурье / Г.П. Толстов. М.: Наука, 1980. 384 с.
5.Пискунов, Н.С. Дифференциальное и интегральное исчисления: в 2 т. Т. 2 / Н.С. Пискунов. М.: Интеграл-Пресс, 2007. 544 с.
88

Приложение
Варианты расчётно-графических работ
Вариант № 1
1. Используя различные признаки, исследовать на сходимость положи-
тельные ряды: |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n 1 |
|
3 |
( 1)n 1 sin n |
|
|
ln n |
|
|||||||||||||
1) |
|
|
|
; |
2) |
|
|
|
|
|
|
; |
3) |
|
|
|
|
|
; |
||
|
|
|
|
2 n 1 |
|
|
|
2 |
1 |
||||||||||||
n 2 |
n 3 |
|
n 1 |
|
|
|
n 2 n |
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
3n |
|
n |
|
|
n2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4) n 3n 1 ; |
5) |
n 2 |
|
; |
6) ne n . |
||||||||||||||||
|
|||||||||||||||||||||
n 1 |
|
|
n8 1 |
n 1 |
n 5 |
n 3 |
|
|
n 1 |
|
|
|
|
|
|||||||
2. Исследовать на сходимость и абсолютную сходимость знакочередующийся ряд
|
n |
|
n 3 |
|
( 1) |
|
ln |
n 1 |
. |
n 2 |
|
|
|
3. Найти область сходимости ряда |
|
|
|
|
||
|
n2 5n |
2x 1 n |
||||
|
|
|
|
|
|
. |
9 |
n |
1 |
3 |
|||
n 1 |
|
|
|
|||
4.Разложить в ряд Маклорена функцию
xarctg 2x 5 . 10x 1
5.Вычислить с точностью до 0, 001 интеграл
|
|
|
|
|
1 ln (1 |
x |
) |
|
|
|
|
||
|
|
|
|
|
5 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
6. |
Найти решение задачи Коши |
|
|
|
|
|
|
|
|||||
|
y |
|
2x y |
|
4 y 0 |
, |
|
|
|
1, |
|
|
|
|
|
|
y(0) 0, y (0) |
|
|
||||||||
представив его в виде разложения в ряд Маклорена. |
|
|
x . |
||||||||||
7. |
Разложить в ряд Фурье на интервале |
( ; ) функцию |
f (x) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
89
Вариант № 2
1. Используя различные признаки, исследовать на сходимость положительные ряды:
|
n 1 |
2n |
|
|
|
arctg (2 ( 1)n ) |
|
ln (2n 1) |
|
|
|||||||||||
1) |
|
|
|
; |
|
|
2) |
|
3n |
1 |
|
; 3) |
|
n |
3 |
5 |
; |
|
|||
|
|
|
|
|
|
|
|
||||||||||||||
n 1 |
n 4 |
|
|
|
|
n 1 |
|
|
n 1 |
|
|
|
|
||||||||
|
|
31 ln (1 |
1 ) ; |
|
|
|
n |
|
|
n2 |
|
|
|
1 |
|
|
|||||
4) |
|
|
|
; 6) |
|
|
. |
||||||||||||||
|
5) |
2n 1 |
|
n 2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n 4 |
|
n 3 |
|
|
|
|||||||
n 1 |
|
|
n |
|
|
n |
|
n 1 n ln (3n 1) |
|
||||||||||||
2. Исследовать на сходимость и абсолютную сходимость знакочередующийся ряд
|
n |
|
|
( 1)n 1 |
. |
||
|
|||
n 1 |
n 30 |
||
3. Найти область сходимости ряда
|
2 n |
|
2x 1 |
|
n |
|
|||||
|
. |
||||
|
|
|
|
|
|
n 1 |
n 4 2x 1 |
|
|||
4. Разложить в ряд Маклорена функцию
8 26 x2 . x
5. Вычислить с точностью до 0, 001 интеграл
1 sin x dx .
0 x
6. Найти решение задачи Коши
y 3x2 y 1 , y(0) 0, y (0) 2 ,
представив его в виде разложения в ряд Маклорена.
7. Разложить в ряд Фурье на отрезке [ 1;1] функцию f (x) x2 .
90
