
1594
.pdf
|
|
|
|
Аналогично доказывается, |
что |
сумма ряда an bn равна |
A B (в |
|
|
n 1 |
|
|
|
|
|
предположении, что оба ряда |
an |
и bn сходятся). |
|
|
n 1 |
n 1 |
|
Таким образом, над сходящимися рядами можно выполнять обычные арифметические операции, такие же, как и над конечными суммами: умножать их почленно на число, складывать и вычитать.
З а м е ч а н и е. Отметим, что сумма сходящегося и расходящегося рядов всегда является расходящимся рядом. О сумме двух расходящихся рядов ничего определённого сказать нельзя.
3. Пусть дан ряд
an a1 a2 ... an ... .
n 1
Предположим, что он сходится. Тогда для любого фиксированного натурального k сходится и ряд
|
|
|
|
|
|
|
|
|
an ak 1 ak 2 ... |
an ... , |
(1.4) |
||||
|
n k 1 |
|
|
|
|
|
|
полученный из исходного ряда отбрасыванием первых k |
слагаемых и назы- |
||||||
|
|
|
|
|
|
|
|
ваемый остатком ряда an после k -го члена (понятие остатка ряда исполь- |
|||||||
|
n 1 |
|
|
|
|
|
|
зуется и для расходящихся рядов). |
|
|
|
n |
|
||
|
|
|
|
|
|
|
|
Д о к а з а т е л ь с т в о. По условию lim Sn lim |
ak S . Фиксируем |
||||||
|
|
n |
n |
k 1 |
|||
произвольное натуральное k, и пусть S a a |
|
|
|||||
2 |
... a |
. Тогда для любого |
|||||
|
|
1 |
|
|
k |
|
|
натурального n k |
справедливо равенство Sn S n k |
, |
где Sn частичная |
||||
сумма всего ряда, |
а n k ak 1 |
ak 2 ... an |
- |
частичная сумма ряда с от- |
|||
брошенными членами. Ясно, что |
|
|
|
|
|
||
и потому |
|
n k Sn S , |
|
|
|
|
|
lim n k lim Sn S S S , |
|
|
|||||
|
|
|
|||||
|
n |
n |
|
|
|
|
|
т.е. ряд с отброшенными членами также сходится.
4. Предположим теперь, что для некоторого натурального k сходится ряд вида (1.4), так что существует конечный предел
lim n k .
n
11
Тогда сходится и ряд an .
n 1
Д о к а з а т е л ь с т в о. Используя равенство n k Sn S , справедливое для любого натурального n k , получаем Sn S n k . Отсюда следует, что
существует конечный предел
lim Sn lim |
S n k S lim n k S , |
|
n |
n |
n |
и потому ряд an сходится.
n 1
Из установленных свойств рядов 3 и 4 следует, что добавление или отбрасывание конечного числа слагаемых не влияет на сходимость ряда.
1.4. Положительные ряды и признаки их сходимости
Рассмотрим достаточные признаки сходимости (расходимости) рядов с неотрицательными членами. В дальнейшем мы будем называть такие ряды положительными.
1. Первый признак сравнения. Пусть даны два положительных ряда
|
|
an , an 0, |
(1.5) |
n 1 |
|
|
|
bn , bn 0, |
(1.6) |
n 1
ипусть an bn , n 1, 2, 3, ... . Тогда из сходимости ряда (1.6) следует сходи-
мость ряда (1.5), а из расходимости ряда (1.5) следует расходимость ряда
(1.6).
Д о к а з а т е л ь с т в о. Поскольку для любого натурального k справедливо неравенство ak bk , то частичные суммы SnA и SnB рядов (1.5) и (1.6) связаны соотношением
SnA SnB , n N .
Пусть ряд (1.6) сходится, тогда существует конечный предел lim S B S B .
n n
Заметим, что частичные суммы рядов образуют возрастающие последовательности. Из свойств возрастающих последовательностей следует, что
12
SnB S B . Таким образом, для любого натурального n выполняется неравенство SnA SnB S B , т.е. возрастающая последовательность SnA ограничена
сверху. Из теории пределов монотонных последовательностей известно, что всякая возрастающая ограниченная сверху последовательность сходится, т.е.
существует конечный предел lim S A S A . А это и означает, что ряд (1.5) схо-
n n
дится.
Пусть теперь ряд (1.5) расходится. Тогда расходится и ряд (1.6), поскольку из его сходимости, в силу уже доказанного, следовала бы сходимость ряда (1.5), а он, по предположению, расходится.
2. Второй признак сравнения. Пусть даны два положительных ряда
|
|
an , an 0, |
(1.7) |
n 1 |
|
|
|
bn , bn 0 , |
(1.8) |
n 1 |
|
и пусть существует предел |
|
lim an K , где 0 |
K . |
n b |
|
n |
|
Тогда
1)если ряд (1.8) сходится и K , то ряд (1.7) также сходится;
2)если ряд (1.8) расходится и K 0, то расходится и ряд (1.7).
Таким образом, если K есть положительное число, то оба ряда сходятся или расходятся одновременно.
До к а з а т е л ь с т в о
1.Пусть ряд (1.8) сходится, и пусть K . Поскольку K число, то после-
довательность |
|
an |
является сходящейся и, как следствие, ограниченной. |
||||||
|
|||||||||
|
|
|
bn |
A 0 такое, |
|
|
|||
Поэтому существует число |
что все члены последовательности |
||||||||
|
an |
будут принадлежать отрезку [0 ; A], |
и потому для любого n N будет |
||||||
|
|||||||||
bn |
|
|
|
an |
|
|
|
||
выполняться |
неравенство |
A, которое равносильно |
неравенству |
||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
an A bn . Поскольку ряд |
bn |
сходится, то сходится и ряд |
A bn . Ис- |
||||||
|
|
|
|
|
|
n 1 |
|
|
n 1 |
пользуя первый признак сравнения, получаем, что ряд (1.7) также сходится.
13

2. Пусть теперь ряд (1.8) расходится, и пусть K 0. Так как K 0, то существует конечный предел
lim |
bn |
|
1 |
. |
|
|
|||
n an |
|
K |
||
Если бы ряд (1.7) сходился, то в силу уже доказанного сходился бы и ряд (1.8), а он, по предположению, расходится. Поэтому ряд (1.7) также расходится.
Пр и м е р ы
1.31n .n 1
Для сравнения воспользуемся гармоническим рядом 1 . Поскольку для
n 1 n
любого n N выполняется неравенство
31n n1
и гармонический ряд, как было замечено ранее, расходится, то, согласно пер-
вому признаку сравнения, ряд 1 также будет расходиться.
n 1 3 n
|
1 |
|
|
|
|
2. |
. |
|
|
||
2 |
|
|
|||
n 1 |
n |
|
|
||
|
|
|
1 |
|
|
Для сравнения рассмотрим сходящийся ряд |
1 (такой ряд был |
||||
n n 1 |
|||||
|
|
n 1 |
|
||
рассмотрен ранее). Воспользуемся вторым признаком сравнения:
lim an |
lim |
n n 1 |
1, K 1. |
|
n2 |
||||
n b |
n |
|
||
n |
|
|
|
Данный ряд сходится по второму признаку сравнения.
3. ln3n .
n 1 n
Для сравнения воспользуемся сходящимся рядом 12 . Заметим, что
n 1 n
14

lim an lim ln n 0, |
K 0. Получаем, |
что по второму признаку сравнения |
|||||||||||||||||||
n b |
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рассматриваемый ряд сходится. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
n ln n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n 1 |
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для |
|
сравнения |
|
рассмотрим гармонический ряд |
|
|
|
|
Поскольку |
||||||||||||
|
|
1 . |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n |
|
|
|
|
|
|
|
|
a |
|
|
|
|
n2 ln n |
|
|
|
n2 |
ln n |
|
|
|
ln n |
|
|
|||||
lim n lim |
|
|
|
|
|
(это следует |
из неравенства |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 1 |
|
||||||||||
n bn |
n n2 |
n 1 |
|
|
|
n2 n 1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
n2 |
|
|
|
ln3n ), то K и по второму признаку сравнения рассматриваемый ряд расходится.
5. |
1n 1 |
|
1 |
0 |
1 1 |
|
1 |
2 ... |
|
|
|
|
1n 1 ... . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n 2 |
|
1 2 |
|
|
2 2 |
|
3 2 |
|
|
|
|
|
|
|
|
n 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
Сравним заданный ряд с рядом |
|
. Заметим, что для любого |
n N |
|||||||||||||||||||||
2 |
n 1 |
|||||||||||||||||||||||
выполняется неравенство |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
n 2n 1 |
|
2n 1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ряд |
|
является сходящимся, поскольку он составлен из членов геомет- |
||||||||||||||||||||||
|
n 1 |
|||||||||||||||||||||||
n 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рической прогрессии со знаменателем q 12 (| q | 1). По первому признаку сравнения рассматриваемый ряд также сходится.
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
. |
|
|
|
|
|
|
|
|
|
|
|
5n 1 |
|
|
|
|
|
|
|
|
|
|
|||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
. Поскольку |
Для сравнения воспользуемся гармоническим рядом 1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n |
|
|
|
|
lim an |
lim |
n |
|
|
1 |
, K |
1 |
, |
|
|
|
|
|
5n 1 |
5 |
5 |
|
|
||||||
|
|
|
n b |
n |
|
|
|
|
|
||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
и гармонический ряд расходится, то заданный ряд также расходится по второму признаку сравнения.
15
Вывод: при использовании признаков сравнения необходимо иметь «запас» рядов, сходимость или расходимость которых заранее известна. Для сравнения, как правило, используются ряды, составленные из членов геометрической прогрессии, гармонический ряд, различные варианты обобщённогармонического ряда.
Рассмотрим достаточные признаки сходимости (расходимости) рядов, которые позволяют исследовать ряды, не прибегая к помощи вспомогательных рядов.
Признак Даламбера. Пусть дан ряд с положительными членами
|
и пусть lim an 1 |
. Тогда: |
an , an 0, |
||
n 1 |
n an |
|
1)при 1 ряд сходится;
2)при 1 ряд расходится;
3)при 1 ряд может как сходиться, так и расходиться (требуется дополнительное исследование).
До к а з а т е л ь с т в о
1.Пусть 1. Выберем число 0 таким, чтобы выполнялось неравен-
ство |
1, и положим |
q . По выбранному |
0 найдём номер |
|||
n0 = n0 ( ) |
такой, чтобы для всех номеров n n0 выполнялось неравенство |
|||||
|
|
|
an 1 |
|
, |
|
|
|
|
|
|
||
|
|
|
an |
|
|
|
равносильное двойному неравенству
an 1 . an
Тогда для любого n n0 будет выполняться неравенство
an 1 an qan .
Далее запишем:
an 1 qan , n n0 , n0 1, n0 2, ... ,
откуда получаем:
an0 1 qan0 ,
16
an0 2 qan0 1 q2an0 ,
an0 3 q3an0 , ... , an0 m qman0 , ... .
Таким образом, члены ряда
an 1 |
an |
2 |
an |
3 |
... an m ... |
(1.9) |
0 |
0 |
|
0 |
|
0 |
|
не превосходят соответствующих членов ряда |
|
|||||
an |
q an |
q2 an |
q3 .... an qm ... |
(1.10) |
0 |
0 |
0 |
0 |
|
Ряд (1.10) представляет собой сумму геометрической прогрессии с первым членом an0 q и знаменателем 0 q 1. Этот ряд сходится. Тогда по первому
признаку сравнения ряд (1.9) также будет сходиться. Но ряд (1.9) получен из
исходного ряда an путём отбрасывания его первых n0 членов. Следова-
n 1
тельно, ряд an сходится.
n 1
2.Пусть 1, и пусть сначала число. Выберем 0 таким, чтобы
выполнялось неравенство 1, и положим q . Повторяя рассуждение первого пункта доказательства, по выбранному 0 найдём номер
n1 n1 |
( ) такой, чтобы для |
всех номеров n n1 выполнялось неравенство |
an 1 |
an qan , q 1. |
Из последнего неравенства следует, что члены |
ряда неограниченно возрастают при увеличении номера n , а это противоре-
чит необходимому признаку сходимости числовых рядов. Поэтому в рассматриваемом случае ряд расходится. Пусть теперь . В этом случае
для любого фиксированного числа q1 1 для всех номеров n , начиная с некоторого, будет выполняться неравенство an 1 q1an . Таким образом, члены ряда неограниченно возрастают с увеличением n и в этом случае. Необходимое
условие сходимости ряда не выполняется, и потому ряд расходится и при
.
3. Пусть 1. В этом случае примеры показывают, что ряд может как
сходиться, так и расходиться, необходимо прибегать к дополнительному исследованию ряда при помощи других признаков.
17

П р и м е р ы
1. 1 .
n 1 n!
Воспользуемся признаком Даламбера:
lim |
an 1 |
lim |
n! |
|
lim |
1 |
|
0 , |
1. |
|
n 1 ! |
|
|
||||||
n an |
n |
n n 1 |
|
|
|||||
По признаку Даламбера ряд сходится.
2. nn .
n 1 n!
Воспользуемся опять признаком Даламбера:
|
a |
|
|
|
|
n 1 n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
n 1 |
|
|
n 1 |
n |
|
n 1 |
|
n! |
|
|
n 1 n |
|
|
|
n |
|||||
lim |
|
n 1 |
lim |
|
|
|
|
lim |
|
|
|
|
|
|
|
lim |
|
|
n |
lim 1 |
|
|
e, |
||
|
n 1 ! n |
n |
|
|
n! n 1 n |
n |
|
|
n |
n |
|||||||||||||||
n |
an |
n |
|
|
n |
|
|
|
|
n |
|
|
n |
|
|
||||||||||
1.
По признаку Даламбера ряд расходится.
|
1 |
|
|
|
|
|
|
|
|
|
|
3. |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n 1 |
n |
|
|
|
|
|
|
|
|
|
|
В рассматриваемом примере |
|
|
|
|
|
|
|
||||
|
|
lim an 1 |
lim |
|
n |
lim |
|
1 |
|
1, |
1. |
|
|
|
n 1 |
|
|
|
|||||
|
|
n an |
n |
n |
1 |
|
1 |
|
|
||
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Ранее было показано, что этот ряд расходится.
4. |
n |
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В данном примере, как и в предыдущем, |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
a |
|
|
|
|
|
|
|
3 |
|
|
1 n |
|
1 |
3 |
|
|
|||
|
|
|
|
|
|
|
n 1 |
n 1 |
|
|
|
|
|
|
|
|
1. |
||||
lim |
|
n 1 |
lim |
|
|
lim 1 |
|
|
|
|
|
|
1, |
||||||||
|
|
n n 2 |
3 |
|
n |
|
|
2 |
|
||||||||||||
n |
an |
|
n |
|
|
|
n |
n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18

|
n |
|
|
n |
|
1 |
|
|
Из очевидного неравенства an |
|
|
|
bn |
и сходимости ряда bn |
|||
(n 1) |
3 |
3 |
2 |
|||||
|
|
|
n |
n |
n 1 |
|||
по первому признаку сравнения получаем, что рассматриваемый ряд сходится.
Радикальный признак Коши. Пусть дан положительный ряд
|
|
an , an 0 |
, и пусть lim n an .Тогда: |
n 1 |
n |
|
1)при 1 ряд сходится;
2)при 1 ряд расходится;
3)при 1 ряд может как сходиться, так и расходиться (требуется дополнительное исследование).
Доказательство аналогично доказательству предыдущго признака. Отметим лишь, что в случае 1 члены ряда неограниченно возрастают при n .
З а м е ч а н и е. Приведённые признаки Даламбера и Коши сходимости положительных рядов называются признаками в предельной форме. Признаки Даламбера и Коши в иной форме, называемой непредельной, можно найти в [1, с.452].
П р и м е р
|
|
n |
|
n |
|
|
|
||||
Исследовать на сходимость ряд |
|
. |
|||
3n 2 |
|||||
n 1 |
|
|
|
||
Воспользуемся радикальным признаком Коши:
lim n an |
lim |
n |
|
1 |
, 1. |
|
3n 2 |
3 |
|||||
n |
n |
|
|
По радикальному признаку Коши ряд сходится.
Интегральный признак Коши. Пусть дан положительный ряд an ,
n 1
члены которого образуют убывающую последовательность. Пусть далее функция f x является непрерывной, положительной и убывающей на
полупрямой x 1, и пусть an f n , n 1,2,3, ... . Тогда данный ряд и
несобственный интеграл f x dx сходятся или расходятся одновременно.
1
19
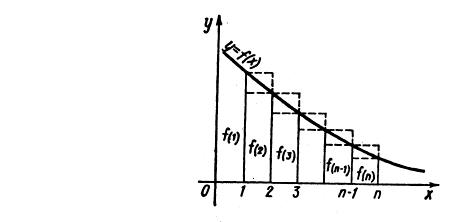
Рис. 1. К доказательству интегрального признака Коши
Д о к а з а т е л ь с т в о. Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции f x , снизу осью Ox , с боков отрез-
ками прямых x 1 и x n . Впишем в эту трапецию и опишем около неё две
ступенчатые фигуры, |
состоящие из прямоугольников с основаниями |
[1;2],[2;3], ... ,[n 1;n] |
и высотами f (1), f (2), f (3), ... , f (n 1), f (n) (рис.1). |
Учитывая геометрический смысл определенного интеграла (интеграл от неотрицательной функции равен площади соответствующей криволинейной трапеции), можно записать:
|
|
|
|
|
|
|
|
|
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn f x dx Sn , |
||||||||||
|
|
|
1 |
|
|
|
|
||||||
где |
|
- площадь вписанной в трапецию фигуры, |
|
||||||||||
|
|
|
|
||||||||||
Sn |
Sn - площадь описанной |
||||||||||||
около трапеции фигуры. Заметим, что |
|||||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
Sn f 2 f 3 ... f n Sn f 1 , |
||||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn f 1 f 2 ... f n 1 Sn f n , |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Sn |
f 1 f 2 ... f n n -я частичная сумма ряда an . |
||||||||||||
n 1
Имеем
n
Sn f 1 f x dx Sn f n .
1
Из полученного двойного неравенства вытекает справедливость каждого из неравенств
n f x dx f n Sn , |
(1.11) |
1
20
