Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1594

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

791.65 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

(n m) x

sin

(n m)

Аналогично доказывается равенство нулю остальных интегралов. Установим, наконец, справедливость равенств

1 2

2 n x

n x

cos

dx l ,

sin

dx l , n N .

Первое из них, не содержащее тригонометрических функций, очевидно. Далее имеем

l	2 n x			1	l
cos			dx		1	cos
		l		2
l					l

2n x		1	l		2n x
	dx l			cos		dx l ,
l	dx l	2		cos	l	dx l ,
l		2			l

			l

l	2 n x			1	l
sin			dx		1	cos
		l		2
l					l

					0
2n x		1	l		2n x
	dx l			cos		dx l .
l	dx l	2		cos	l	dx l .
l		2			l

			l
					0

2.3.3. Коэффициенты и ряд Фурье

Пусть при каждом x [ l ; l] тригонометрический ряд (2.32) сходится. Тогда его сумма является функцией от переменной x . Обозначив её черезF(x) ,

можно записать	a			n x		n x

F x		0	an cos		bn sin		.
	2			l		l
			n 1

Очевидно, что в рассматриваемом случае ряд (2.32) сходится при любом x E1 , а его сумма F(x) на самом деле является 2l - периодической функцией, определённой на всей вещественной оси. Поэтому записанное равенство выполняется при любом x E1 .

Определение. Если функция f (x) , определённая на промежутке [ l ; l] ,

является на этом промежутке суммой тригонометрического ряда (2.32), так что справедливо равенство

	a				n x		n x
f (x)		0	an cos			bn sin		,	(2.34)
f (x)	2		an cos		l	bn sin	l	,	(2.34)
	2		n 1		l		l
то говорят, что функция	f (x) разлагается на промежутке								[ l ; l] в тригоно-
метрический ряд.			f (x)	разлагается на промежутке [ l ; l] в триго-
Ясно, что если функция			f (x)	разлагается на промежутке [ l ; l] в триго-

нометрический ряд, то с необходимостью выполняется условие f ( l) f (l). Теорема. Пусть функция f (x), определённая и непрерывная на отрезке [ l ; l], разлагается на этом отрезке в тригонометрический ряд (2.34), кото-

рый обладает следующими свойствами: можно интегрировать почленно сам ряд и ряды, получающиеся из данного умножением его на произвольную функцию тригонометрической системы. Тогда коэффициенты a0 , an ,bn , n 1, 2,... находятся по формулам

	a 1 l		f x dx ,
	0	l l

a	1 l	f x cos			n x		dx ,	(2.35)

n	l l				l

b	1 l	f x sin		n x		dx ,

n	l l				l

n 1, 2, ... .

До к а з а т е л ь с т в о. Проинтегрируем равенство (2.34) в пределах от

l до l :

n x

f x dx

dx an cos

bn sin

a0 l

n 1

a 1 l

f x dx.

l l

Фиксируем далее произвольный номер m , умножаем равенство (2.34) на cos ml x и интегрируем получившееся равенство от l до l :

m x

n x

m x

x cos

cos

dx ( an

cos

n 1

n x

m x

sin

cos

dx)

cos2

dx b

sin

cos

n x

m x

n x

m x

(an

cos

sin

cos

dx) am l

n 1

n m

(символом обозначена

сумма,

не

содержащая

слагаемого

с номером

n 1

n m ).

n m

Получаем:

1 l

f x cos

m x

dx, m 1,2, ... .

l l

Аналогично умножая равенство (2.34) на sin

m x

и интегрируя получив-

шееся соотношение по отрезку l; l , получаем формулу

1 l

f x sin m x dx , m 1, 2,... .

l l

Доказанная теорема даёт основание ввести следующее

Определение. Пусть f (x) функция, определённая и интегрируемая на

отрезке	l; l . Тригонометрический ряд, коэффициенты которого определя-
ются	формулами (2.35),			называется		рядом		Фурье, а числа
a0 , an , bn , n 1, 2,... коэффициентами Фурье функции f (x).
При этом пишут		a			n x		n x
	f x
			0	an cos	l	bn sin	l
		2		n 1

(заметим, что ряд Фурье функции f (x) может и не иметь суммой функцию f (x) ).

Функция вида

Sn (x) Sn (x ; f ) a0	(ak cos k x		bk sin k x ),	n 1,2,...
	n
2	k 1	l	l

называется n й суммой Фурье функции f (x) , при этом S0 (x) a20 .

2.3.4. Сходимость ряда Фурье

Ответ на вопрос о сходимости ряда Фурье даёт приводимая ниже теорема. Напомним сначала понятие кусочно-дифференцируемой (кусочногладкой) функции, для которой и будет сформулирован результат о сходимо-

сти.

Пусть функция f (x) кусочно-непрерывна на отрезке [a;b], т.е. существу-

ет разбиение	{x }i k	,	a x	x ... x	k	b этого отрезка такое, что функция
	i i 0		0	1	k

f (x) непрерывна на каждом интервале (xi 1 ; xi ), i 1,..., k, и существуют ко-
нечные односторонние пределы	f (xi 0), f ( xi 0),			i 1,..., k 1,	f ( x0 0)
f (a 0) , f (xk 0) f (b 0). Пусть далее для каждого индекса					i 1, 2,..., k
функция
	f (x), xi 1 x xi ,
fi (x) f (xi 1		0),	x xi 1 ,
	f (xi	0),	x xi

дифференцируема на отрезке [xi 1; xi ]. Тогда функция f (x) называется кусоч- но-дифференцируемой (кусочно-гладкой) на отрезке [a;b].

Справедливо следующее утверждение.
Теорема. Пусть функция f x		кусочно-дифференцируема			на отрезке
l; l . Тогда ряд Фурье функции f		x в каждой точке x ( l ;l)			сходится и
его сумма равна
	f (x 0) f (x 0)		.

		2
В частности, в точках непрерывности функции f x её ряд Фурье сходится к
значению функции f x в этой точке. В точках x l и				x l	ряд также
сходится и имеет своей суммой число

f ( l 0) f (l 0) . 2

З а м е ч а н и е. Пусть функции f x , кусочно-дифференцируемой на отрезке l; l , соответствует ряд Фурье

a			n x		n x
	0	an cos		bn sin		.
2		an cos	l	bn sin	l	.
2		n 1	l		l

В силу приведённой теоремы данный ряд сходится в каждой точке отрезкаl; l . Как уже было отмечено ранее, в этом случае рассматриваемый ряд

будет сходиться в каждой точке числовой прямой. Пусть F(x) его сумма. Ясно, что F(x) представляет собой 2 l периодическую функцию, которая на отрезке l; l задаётся соотношениями

	f (x 0) f (x 0)				, x ( l ;l),
					, x ( l ;l),
	2
	2
		f ( l 0)		f (l 0)
		f ( l 0)		f (l 0)
F(x)						, x l		,
F(x)	2					, x l		,
	2			f (l 0)
			f ( l 0)	f (l 0)			, x l .

	2
	2

2.3.5. Неполные ряды Фурье

Ряды Фурье для чётных и нечётных функций

Пусть x		чётная функция на отрезке l ; l , т.е.	x x
x l ; l .

Рис. 4. График чётной функции x , заданной на отрезке l ; l

Тогда, учитывая геометрический смысл определённого интеграла, получаем:

l	x dx 2 l	x dx
l	0

(площадь криволинейной трапеции, составленной из двух равных по площади трапеций, симметричных относительно оси Ox , равна удвоенной площади любой из этих трапеций).

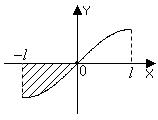
Пусть теперь x нечётная функция, заданная на отрезке l ; l , так что x x x l ; l .

Рис. 5. График нечётной функции ( x) , заданной на отрезке l ; l

Тогда

x dx 0

(интеграл от нечётной функции по симметричному относительно точки x 0

интервалу равен разности площадей равновеликих плоских фигур, т.е. нулю). Заметим ещё, что произведение двух чётных или нечётных функций является чётной функцией, а произведение чётной и нечётной функций нечёт-

ной функцией.

Поэтому при разложении чётной функции f x в ряд Фурье следует учесть, что

		a0	1 l	f	x dx	2 l	f x dx ,	(2.36)
			l l			l 0
an	1 l	f x cos n x dx				2 l	f x cos n x dx ,	(2.37)
	l l				l	l 0	l
		b	1 l		f x sin n x dx 0 ,			(2.38)
		n	l l			l
			l l			l

n 1, 2, ... .

В результате для

x получаем неполный ряд Фурье по косинусам

f x a0

n x

an cos

(2.39)

n 1

коэффициенты которого определяются по формулам (2.36) и (2.37).

Пусть теперь f x

нечётная функция, тогда

1 l

f x dx 0 ,

(2.40)

l l

an 1 l

f x cos

n x

dx 0 ,

(2.41)

l l

1 l

f x sin

n x

dx 2 l

f x sin

n x

dx ,

(2.42)

l l

l 0

n1, 2, ... .

Врезультате получаем неполный ряд Фурье по синусам

	n x
f x bn sin	n x	,	(2.43)
f x bn sin	l	,	(2.43)
n 1	l
в котором коэффициенты bn определяются по формуле (2.42).
П р и м е р ы
1. Разложить в ряд Фурье на интервале ( ; ) функцию f			x x .

В рассматриваемом случае l . Найдём коэффициенты Фурье функции f x x . Поскольку f x нечётная функция, то все коэффициенты an , n 0,1, 2, ... равны 0, а коэффициенты bn , n 1, 2, 3, ... находятся по формуле

	1		n x		1		2		2
bn		f x sin		dx		x sin nxdx		x sin nxdx		xd ( cos nx )

								0		0	n

2n x cos nx

Таким образом,

		2			2		2			2		n
		2			2		2			2		n
			cos nx dx n cos n					sin nx		n	( 1)
0		n					n2	sin nx	0		( 1)
0		n					n2		0
			0
							0
	2		( 1)n 1	2	( 1)n 1	, n 1,2, ... .
	2		n	2	n	, n 1,2, ... .
			n		n

		n 1
f (x) 2 ( 1)		sin nx ,
n 1	n

при этом справедливо равенство

				n 1
	x 2 ( 1)			sin nx , x .	(2.44)
		n 1	n
	( 1)	n 1
Пусть F (x) 2	( 1)	sin nx , x . Тогда F(x) x при x , а
n 1	n
F( ) F( ) 0.	График 2 периодической функции F(x) изображён на

рис. 6.

Рис. 6. График функции F ( x) суммы ряда Фурье функции f (x) x

Положив в формуле (2.44)	x	, получим равенство
		2
				n 1
	2 ( 1)			sin n .	(2.45)
2		n 1	n	2

Заметим, что все члены ряда из формулы (2.45) с чётными номерами n

равны 0.	Рассмотрим теперь члены этого ряда с нечётными номерами
n 2k 1,	k N . Имеем:

( 1)n 1

sin

( 1)2k 2

sin (2k 1)

sin (k

)

2k 1

( cos k )

( 1) ( 1)k

( 1)k 1

( 1)k 1.

2k 1

Поэтому равенство (2.45) можно записать в виде

2 (

1)k 1

1 .

k 1

2k 1

Из последнего соотношения получаем:

( 1)n 1

n 1

2n 1

2. Разложить в ряд Фурье на отрезке

; функцию

x x2 .

Данная функция является чётной, и потому в результате разложения её в ряд Фурье получим неполный ряд по косинусам. Вычислим её коэффициенты Фурье an :

													2							2x3							2 2

								a0						x2dx															,
								a0						x2dx						3							3		,
														0						3				0			3
														0										0

		2		2					2				2		sin nx							2					2 sin nx					2
		2		2					2				2		sin nx							2					2 sin nx					2
an			x		cos nxdx						x			d (			n		)						x			n				n	x sin nxdx
an			x		cos nxdx						x			d (			n		)						x			n				n	x sin nxdx
			0								0																				0		0
			0								0																				0		0
																											0

4						4						cos nx						4					cos nx							1
4						4						cos nx						4					cos nx							1
	x sin nxdx							xd (								)					x											cos nxdx
	x sin nxdx							xd (								)					x											cos nxdx
n 0						n 0							n					n								n		0		n		0
n 0						n 0							n					n								n		0		n		0

							4			cos n								4															0
							4											4		1 n , n 1,										2,... .
							n											n2		1 n , n 1,										2,... .
							n						n					n2

Таким образом, получаем следующее разложение в ряд по косинусам:

x2	2		12	n

		4		cos nx , x	(2.46)
3		n 1	n
(равенство выполняется и в граничных точках x и					x , поскольку
F( ) F( ) ( f ( 0) f ( 0)) / 2				( f ( ) f ( )) / 2 f ( ) f ( ) ).

Рис. 7. График суммы ряда Фурье F (x) функции f x x2

Интересно отметить, что, подставив x 0 в формулу (2.46), получим ра-

венство														1 n
				0			2							1 n
				0					3		4				n	2	,
из которого следует формула									3			n 1			n
из которого следует формула
1	1		1			1		+ ... ( 1)n 1									1		+ ...= 2 .
1	2		2			2		+ ... ( 1)n 1									2		+ ...= 2 .
2		3				4											n				12
Подставив же в формулу (2.46)										x , получим равенство
											2					1
					2							4				1		,
					2					3		4				2		,
										3			n 1			n
из которого следует, что
			1		1					1	...			1		...				2	.
			1	2		2				2	...			n	2	...				6	.
				2					3					n						6
Ряд Фурье для функции, определённой на отрезке 0; l
Пусть функция f (x)		задана только на отрезке 0; l . Требуется разложить
в ряд Фурье на отрезке l ; l						некоторую функцию f (x) такую, чтобы сумма
её ряда Фурье на отрезке 0; l						(или на интервале (0;l) ) совпадала бы с f (x) .

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.2022766.41 Кб01555.pdf
#
15.11.2022780.68 Кб01571.pdf
#
15.11.2022782.64 Кб01577.pdf
#
15.11.2022786.15 Кб01584.pdf
#
15.11.2022787.95 Кб41587.pdf
#
15.11.2022791.65 Кб01594.pdf
#
15.11.2022793.8 Кб21598.pdf
#
15.11.2022794.89 Кб11601.pdf
#
15.11.2022795.19 Кб01603.pdf
#
15.11.2022798.83 Кб21609.pdf
#
15.11.2022805.01 Кб01620.pdf