
1521
.pdf
M А = 0, F 0,5 + M + F 4,5 + RB 4 − q 5 2 = 0,
RB = −10 − 90 − 20 + 100 = −5 кН. 4
Проверка:
Fy = 0, RA − RB − F + F − q 5 = 55 − 5 − F + F − 50 = 0.
Слева:
M xD = −F 2,5 + RA 2 − q 2,5 1,25 = −50 + 55 2 − 31,25 = 28,75 кНм.
Справа:
M xD = F 2,5 − RB 2 − q 2,5 1,25 =50 − 10 − 31,25 = 8,75 кНм.
Для четырех рассмотренных балок разрывы изгибающих моментов в сечении D соответствуют сосредоточенным моментам, приложенным в этом сечении.
Схема 5.
M B = 0, M − M − RA 2 − q 2 3 + q 2 1 + q 2 1 = 0,
= 25 − 25 − 60 + 20 + 20 = −
RA 2 10 кН.
M А = 0, M − M + RB 1 − q 2 1− q 2 1+ q 2 3 = 0,
= −25 + 25 + 20 + 20 − 60 = −
RB 2 10 кН.
Проверка:
RA − RB − q 2 + q 4 = 0.
−10 − 10 − 20 + 40 = 0.
Слева:
M xD = −M − RA 1+ q 2 2 − q 1 0,5 = −25 − 10 + 40 − 5 = 0.
Справа:
M xD = −M − RB 1 + q 2 2 − q 1 0,5 = − 25 − 10 + 40 − 5 = 0.
211
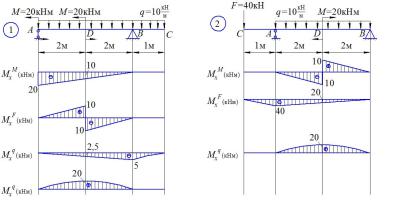
Ответы:
–2
–5
–4
–1
–3
Может быть рассмотрен и другой подход решения этого теста, учитывая, что большинство задач сопротивления материалов решают в предположении линейно деформируемого тела, то есть такого, когда применим закон Гука, при котором предполагается прямая пропорциональность между деформациями и нагрузками.
С учетом гипотез о малости деформаций и линейной зависимости между деформациями и действующими усилиями можно при решении многих задач сопротивления материалов применять принцип независимости и сложения действия сил. По этому принципу усилия в любом элементе конструкции, вызванные различными факторами (несколькими силами), равны алгебраической сумме усилий, вызванных каждым из этих факторов, и не зависят от порядка их приложения. Указанное выше справедливо и в отношении деформаций.
M x = M xi , Qy = Qyi , R = Ri
Построение эпюр изгибающих моментов M xi для пяти предложенных схем нагружения двухопорных балок.
212
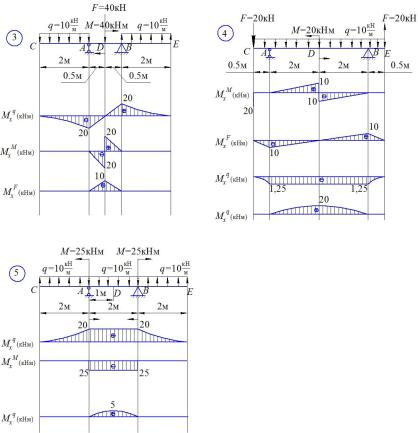
RA
RB
Определение изгибающих моментов в сечении D M x = M xi .
Схема 1.
Слева: M D = −10 + 10 − 2,5 + 20 = 17,5 кНм.
Справа: M D = −10 − 10 − 2,5 + 20 = −2,5 кНм.
= RAM + RAq − RAq = |
2M |
+ |
q 4 |
|
− |
q 1 0,5 |
= 10 + 20 −1,25 = 28,75 кН. |
|||||
|
4 |
|
|
|
|
|||||||
|
|
2 |
|
|
4 |
|
|
|||||
= RBM + RBq + RBq = − |
2M + |
q 4 |
− |
q 1 4,5 |
= −10 + 20 + 11,25 = 21,25 кН. |
|||||||
|
|
|||||||||||
|
|
4 |
2 |
|
4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
213 |
Схема 2.
Слева: M D = −10 − 20 + 20 = −10 кНм Справа: M D = 10 − 20 + 20 = 10 кНм
RA = −RAM + RAF + RAq = −5 + 50 + 20 = 65 кН
RB = RBM − RBF + RBq = 5 − 10 + 20 = 15 кН
Схема 3.
Слева: M D = −20 + 10 = −10 кНм
Справа: M D = 20 + 10 = 30 кНм
RA = −RAM + RAF + RAq + RAq = −40 + 20 + 10 2 2 + 10 2 1 = 40 кН RB = RBM + RBF − RBq − RBq = 40 + 20 − 10 2 1 − 10 2 2 = 0
Схема 4.
Слева: M D = 10 − 1,25 + 20 = 28,75 кНм
Справа: M D = −10 − 1,25 + 20 = 8,75 кНм |
|
|
|
||
RA = RAM + RAF + RAF + RAq = 5 + |
20 4,5 + |
20 0,5 |
+ |
50 = 55 кН |
|
|
4 |
4 |
|
2 |
|
RB = RBM + RBF + RAF + RAq = −5 |
− 20 0,5 |
− 20 4,5 |
+ 50 |
= −5 кН |
|
|
4 |
4 |
|
2 |
|
Схема 5. |
|
|
|
|
|
Слева: M D = 20 − 25 + 5 = 0 |
|
|
|
|
|
Справа: M D = 20 − 25 + 5 = 0 |
|
|
|
|
|
RA = RAM − RAq + RAq = 0 − 40 + |
20 = −10 кН |
|
|
|
|
2 |
2 |
|
|
|
|
так как нагрузки действуют симметрично относительно сечения D RA = RB = −10 кН
Ответы: I – 2
II – 5
III – 4
IV – 1
V – 3
214
ТЕМА 7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ
|
Тест 26 |
|
Решение |
1. Определение реакций в сечении A : |
|
а) Fx = 0, RAГ |
= 0 для схем 1, 2, 3, 4, 6; для схемы 5 RAГ = 2F |
и направлено вправо; |
|
б) |
|
Fy = 0 , сх. 1 |
RAb − 5F = 0, RAb = 5F; |
сх. 2 |
RAb + 2F − 2F = 0, RAb = 0; |
сх. 3 |
RAb − 2F = 0, RAb = 2F; |
сх. 4 |
RAb = 0; |
сх. 5 |
RAb + F = 0, RAb = −F (направлена вниз); |
сх. 6 |
RAb − F = 0, RAb = F; |
в) |
|
M A = 0 , сх. 1 |
M A + 2Fl − 3Fl = 0, M A = Fl |
сх. 2 |
(направлен против часовой стрелки); |
M A − Fl − Fl = 0, M A = 2Fl |
|
сх. 3 |
(направлен против часовой стрелки); |
M A + Fl − 2Fl = 0, M A = Fl |
|
сх. 4 |
(направлен против часовой стрелки); |
M A + 2Fl − 2Fl = 0, M A = 0 |
|
сх. 5 |
M A + 2Fl + Fl = 0, M A = −3Fl |
сх. 6 |
(направлен по часовой стрелке); |
M A + Fl − Fl = 0, M A = 0. |
|
215
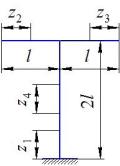
2. Анализ изгибающих моментов ( Mизг ) на участках АС, ВС, DC
сх. 1
сх. 2
сх. 3
сх. 4
сх. 5
сх. 6
Mизг (Z1 ) = −Fl, |
Mизг (Z2 ) = −2F z2 , |
|||
0 ≤ z2 ≤ l |
|
|
|
|
0 ≤ z1 ≤ 2l Mизг (0) = 0, Mизг (l) = −2Fl |
||||
Mизг (Z3 ) = −3Fz3 , 0 ≤ z3 ≤ l, |
|
|||
Mизг (0) = 0, Mизг (l) = −Fl |
|
|||
Mизг (Z1 ) = −2Fl, Mизг (Z2 ) = |
qz22 |
, |
||
|
||||
|
|
2 |
|
|
Mизг (0) = 0, Mизг (l) = Fl |
|
|||
Mизг (Z3 ) = − |
qz32 |
, Mизг (0) = 0, Mизг (l) = −Fl |
||
|
||||
2 |
|
|
|
|
Mизг (Z1 ) = − Fl, |
0 ≤ z1 ≤ l, Mизг |
|
||
(Z4 ) = −2Fl, 0 ≤ z4 ≤ l,
Mизг (Z2 ) = 0, Mизг (Z3 ) = −2Fz3 , 0 ≤ z3 ≤ l, Mизг (0) = 0,
Mизг (l) = −2Fl
Mизг (Z1 ) = 0, Mизг (Z4 ) = −2Fl,
Mизг (Z2 ) = 0, Mизг (Z3 ) = −2Fl
Mизг (Z1 ) = 3Fl − 2F z1 , Mизг (0) = 3Fl, Mизг (l) = Fl, Mизг (Z2 ) = 0,
Mизг (Z3 ) = Fz3 , Mизг (0) = 0,
Mизг (l) = Fl, Mизг (Z4 ) = Fl
Mизг (Z1 ) = 0, Mизг (Z2 ) = −F z2 , Mизг (0) = 0, Mизг (l) = −Fl
Mизг (Z3 ) = −Fl, Mизг (Z4 ) = 0
216
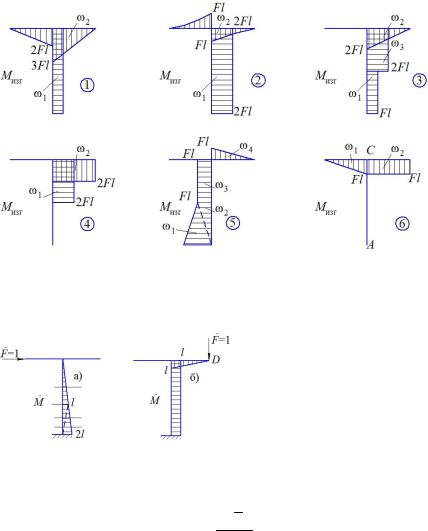
3. Построение эпюр изгибающих моментов от заданных нагрузок:
4. Построение эпюр изгибающих моментов для вспомогательного состояния.
Искомых параметров два: определение перемеще-
ний vВг и vDг . Следовательно,
вспомогательных состояний в которых прикладываются соответствующие единичные усилия.
5. Определение вертикального и горизонтального перемещения для указанных рам способом Верещагина.
= ωi Mci
EJi
217

1. Из перемножения эпюр рис. 1 на эпюру а) рис. 2 по правилу Верещагина следует, что горизонтальное перемещение vВг сечения В равно нулю для схемы 6, так как изгибающий момент ( Mизг ) на участке отсутствует.
2. Наибольшее значение |
vВг |
горизонтального перемещения се- |
||||||||||||||
чения В возможно для второй или пятой рамы. |
|
|
|
|
|
|
||||||||||
Сх. 2 |
vВг = |
|
Fl3 |
(2 2 1) = 4Fl3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
EJ |
|
EJ |
|
|
|
|
|
|
|
|
|||
|
|
Fl3 |
1 3 1 |
5 |
+ 1 |
|
4 |
|
1 |
|
|
11Fl3 |
|
|
||
Сх. 5 |
vВг = |
1 1 |
+1 1 |
= |
|
|||||||||||
|
3 |
3 |
2 |
3EJ |
|
|
||||||||||
|
|
|
EJ 2 |
2 |
|
|
|
|
|
|
||||||
Итак, наибольшее значение горизонтального перемещения сечения В имеем для второй рамы.
|
Значение горизонтального перемещения сечения В по модулю |
|||||||||||||
vВг = |
11Fl3 |
следует для схемы 5. |
|
|
|
|||||||||
|
3EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Определение вертикального перемещения сечения D. |
|||||||||||||
|
Сх. 1 |
vг |
= |
|
Fl3 |
1 |
2 |
1+ |
1 |
3 1 |
2 = 3Fl3 |
|||
|
|
|
|
|
||||||||||
|
|
В |
|
|
EJx |
|
|
2 |
|
3 |
EJ |
|||
|
Сх. 2 |
vDг = |
Fl3 |
2 |
2 |
1+ |
1 |
1 1 |
3 |
|
= 17Fl3 |
|||
|
|
3 |
||||||||||||
|
|
|
|
|
EJ |
|
|
|
4 |
|
4EJx |
|||
Сх. 3 |
vDг = |
Fl3 |
1 |
1 |
1+ |
2 1 1+ |
1 |
2 1 |
2 |
= |
11Fl3 |
|
|
|
|
|
|||||||
|
|
|
2 |
3 |
3EJx |
|
|
|
|
|
|||||||||||||
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Сх. 4 |
vDг = |
|
Fl3 |
2 1 1+ |
2 1 1 = 3Fl3 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
EJ |
|
|
|
2 |
EJ |
|
|
|
|
|
|
|
|
|||||||
|
|
Fl3 |
1 |
3 1 1+ 11 |
|
|
1 1 1 |
|
2 |
|
|
10Fl3 |
|||||||||||
Сх. 5 |
vDг = |
− |
1 |
1+1 1 1+ |
|
= |
|||||||||||||||||
|
|
3 |
3EJ |
||||||||||||||||||||
|
|
|
|
EJ 2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
||||||||
Сх. 6 |
vDг = |
Fl3 |
1 |
1 |
1 |
= |
Fl3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
2EJ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
218
Ответы в соответствии с поставленными вопросами: I – 6.
II – 2.
III – 5.
IV – 5.
V – 6.
219

ПРИЛОЖЕНИЕ 2
РАСЧЕТНЫЕ ФОРМУЛЫ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Растяжение – сжатие:
σmax = |
Nmax |
≤ [σ], |
ε = |
N |
, |
|
l = |
Nili |
. |
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
A |
|
|
|
EA |
|
|
|
|
|
|
E A |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i i |
|
Кручение валов круглого сечения: |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Mкmax |
≤ [τ], |
|
|
|
|
|
Mкmax |
[θ], |
|||||||||
τmax = |
|
|
|
|
|
|
θmax = |
|
|
|
≤ |
|||||||||
|
Wp |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
GJ p |
|
|
|
|
|||||||
φ = |
Mкi li |
, |
wp = |
Wp |
, |
jp |
= |
J p |
≤ [τ]. |
|||||||||||
|
|
2 |
||||||||||||||||||
|
|
|
GJ pi |
|
|
A3 |
|
|
|
A |
|
|
|
|
||||||
Кручение валов прямоугольного сечения:
τmax = |
Mкmax |
|
≤ [τ], |
wк = αhb2 , |
||||
Wк |
||||||||
|
|
|
|
|
|
|||
Поперечный плоский изгиб: |
||||||||
|
σmax = |
|
M max Y |
≤ [σ], |
||||
|
|
x |
max |
|||||
|
|
Jx |
||||||
|
|
|
Wx = |
Jx |
, |
τmax = |
||
|
|
|
|
|||||
|
|
|
|
|
Ymax |
|
||
θmax = |
Mкmax |
≤ [θ], Jк = βhb3. |
|
GJк |
|||
|
|
σmax = M x max ≤ [σ], |
||
Wx |
||
Qymax Sxmax |
≤ [τ]. |
|
Jxb( y) |
||
|
||
Определение перемещений при изгибе:
Уравнения начальных параметров
n |
(z − ai ) |
|
n |
|
Fi (z − bi ) |
2 |
|
q(z − c) |
3 |
|
q(z − d) |
3 |
|
|
|
|||||||||||||
EJθ= EJθ0 ± |
Mi |
± |
|
|
+ |
|
− |
|
, |
|
|
|||||||||||||||||
|
1! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
i=1 |
|
|
i=1 |
2! |
|
|
|
|
|
3! |
|
|
|
3! |
|
|
|
|
||||||||||
|
n |
|
Mi (z − ai |
) |
2 |
|
|
n |
(z − bi ) |
3 |
|
q(z − c) |
4 |
|
q(z |
− d) |
4 |
|
||||||||||
EJv = EJv0 + EJθ0 z ± |
|
|
± |
Fi |
|
+ |
|
− |
|
. |
||||||||||||||||||
|
|
|
|
|
3! |
|
|
|
|
|
4! |
|
||||||||||||||||
|
i=1 |
2! |
|
|
|
|
|
i=1 |
|
|
|
|
4! |
|
|
|
|
|
|
|||||||||
220
