249

kowski sum and Minkowski product of two point sets in the Euclidean space En. Minkowski sum linear and matrix combination, Minkowski product linear and matrix combination, and Minkowski arithmetic combination of point sets are introduced and illustrated on examples.

Keywords: Minkowski sum and product, Minkowski linear, matrix and arithmetic combination of point sets.

1. Minkowski linear combinations of two point sets

Concept of Minkowski linear combination of two point sets is an analogy of the well defined concept of a linear combination of two vectors. It can be defined on the basis of the scalar multiple of a vector. Let us introduce the operation of a scalar multiple of a point set.

Definition 1.1. Multiple of a point set A En by scalar k R is point set Ak En with elements in all such points of the space, whose positioning vectors are k- multiples of positioning vectors of all points of the set A

Set Ak is denoted also as dilatation of set A by a non-zero scalar k R, and it can be interpreted geometrically as a homothetic scaled image of the point set A in the homothety with centre in the reference point O and with scaling coefficient k. Symmetric configuration of points in the set A is therefore an invariant property that appears also in the configuration of points in the k-multiple image – point set Ak.

Minkowski linear combination of two point sets can be defined as generalisation of the operation of Minkowski sum of point sets.

Definition 1.2. Minkowski sum linear combination of two point sets A and B in the space En is point set C in the space En defined as follows

Consequence 1.1. Minkowski sum linear combination of two congruent point sets A = B in the space En is set

Proof: C =k.A l.A = Ak Al ={k.a +l.b,a A,b A}= ={k.a +l.a,a A} {k.a +l.b,a A,b A,a≠b}=

={(k +l).a,a A} {k.a +l.b,a A,b A,a≠b}= =(k +l).A {k.a +l.b,a A,b A,a≠b} Ak+l

Consequence 1.2. Minkowski sum of a point set A in the space En with itself is the point set

elib.pstu.ru

Proof: A A={a +b,a A b A}={a +a,a A} {a +b,a A,b A,a ≠b}= ={2a,a A} {a +b,a A,b A,a ≠b} 2.A= A2.

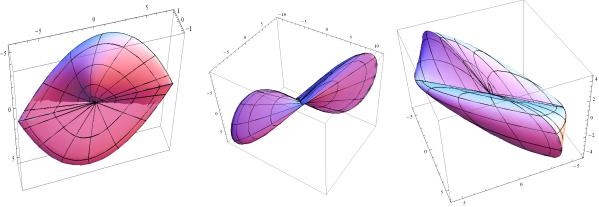
Several illustrations of Minkowski linear combinations of two discrete point sets are presented in Fig. 1, while Minkowski linear combinations of two equally parameterized planar curve segments are in Fig. 2. In Fig 3, Minkowski linear combinations of two curve segments in 3-dimensional space are visualised as surface patches.

Fig. 1. Minkowski sum linear combinations of two discrete point sets

Fig. 2. Minkowski sum linear combinations of two planar curve segments

172

elib.pstu.ru

2. Minkowski matrix combinations of two point sets

Operation of matrix multiple of a point set in En by a suitable matrix can be defined by means of matrix multiplication. Positioning vectors of points in the set in En are matrices of type 1 × n, operation of matrix multiplication can be therefore defined for square matrices of type n × n. Concept of Minkowski sum and product matrix combination can be introduced.

Definition 2.1. Let M =(aij )i, j=1,...,n be a regular square matrix of rank n and A be a non-zero point set in the space En. Multiple of matrix M and set A is point set AM in the space En, defined as

Multiple of a point set A and matrix M can be geometrically interpreted as follows: set AM is the image of point set A in the linear geometric transformation of the space En determined by the respective regular square matrix M. Configuration of points in the set A is mapped in the given transformation into a new configuration, in which e.g. symmetry could be no more invariant.

Definition 2.2. Let A, B be point sets in the space En and M, N be regular square matrices of rank n with real entries. Minkowski sum matrix combination of point sets A, B is point set C in space En

Consequence 2.1. Minkowski sum linear combination of point sets is a special case of Minkowski sum matrix combination, in which both matrices M and N are diagonal matrices with non-zero entries, except those on major diagonals that are equal numbers in respective matrices, k in matrix M and l in matrix N.

Proof: Matrix multiples A.M and B.N of sets A, B and diagonal matrices M, N are

A.M ={a.M,a A},B.N ={b.N,b B}, while for any element a A, or b B the following is valid

A.M ={k.a,a A}= Ak ,B.N ={l.b,b B}=Bl .

Then, Minkowski sum matrix combination of point sets A and B can be written as

AM BN = A.M B.N ={a.M +b.N,a A,b B}= ={k.a +l.b,a A,b B}= Ak Bl =k.A l.B

174

elib.pstu.ru

Examples of Minkowski sum matrix combinations of two finite point sets are in Fig. 5, on Fig. 6 Minkowski sum matrix combinations of equally parameterized planar curves are presented, while in Fig. 7 Minkowski sum matrix combinations of two space curve segments from illustrations in Fig 3 are given.

Fig. 5. Minkowski sum matrix combinations of two discrete point sets

Fig. 6. Minkowski sum matrix combinations of two planar curve segments

Fig. 7. Minkowski sum matrix combinations of two curve segments in 3D

175

elib.pstu.ru

Definition 2.3. Let A, B be point sets in the space En and M, N be regular square matrices of rank n with real entries. Minkowski product matrix combination of point sets A, B is point set C in space En

Consequence 2.2. Minkowski product matrix combination A.M B.N of two point sets A and B in the space En is the M.N matrix multiple of Minkowski product A B of point sets A and B

Proof: A.M B.N = AM BN ={a.M l.N,a A,b B}= ={M.N(a b),a A,b B}=M.N(A B) =(A B)M.N.

In Fig. 8, views of three surfaces are presented, which are generated as Minkowski product matrix combinations of the same two curve segments that are chosen in examples of Minkowski sum and product linear combinations viewed in Fig. 3 and Fig. 4, and Minkowski sum matrix combinations in Fig. 7.

Fig. 8. Minkowski product matrix combinations of two curve segments in 3D

3. Minkowski arithmetic combination of three point sets

Concept of Minkowski arithmetic combination of three sets can be introduced, based on Minkowski sum and.

Definition 3.1. Let A, B, C be point sets in the space En and k, l, h be real numbers. Minkowski arithmetic combination of point sets A, B, C is point set W in space En defined by trhe following formula

Consequence 3.1. Minkowski arithmetic combination (k.A l.B) h.C of three point sets A, B and C in the space En can be represented as the h-multiple of Minkowski sum of Minkowski product linear combinations of sets A and C and B and C

(k.A l.B) h.C =(Ak Bl ) Ch =((A C)k (B C)l )h ,h,k,l R. (3.2)

176

elib.pstu.ru

Proof: (k.A l.B) h.C ={(k.a +l.b) h.c,a A,b B,c C}= ={(k.a h.c)+(l.b h.c),a A,b B,c C}=

=(k.A h.C) (l.B h.C) =k.h(A C) l.h(B C) = =(A C)k.h (B C)l.h =((A C)k (B C)l )h

Consequence 3.2. Minkowski arithmetic combination of three point sets A, B and C in the space En for constants k = l = h multiple of Minkowski product A B of

Minkowski arithmetic combination of three equally parameterized curve segments is a curve segment, examples are visualised in Fig 9. The same three curve segments viewed in Fig. 9 on the left are used for illustration of Minkowski arithmetic combinations in which two curves are equally parameterized. The resulting surface patches can be seen in Fig. 10.

Fig. 9. Minkowski arithmetic combinations of three curve segments

Fig. 10. Minkowski arithmetic combinations of three curve segments in 3D

177

elib.pstu.ru

This paper was supported by the grant VEGA No. 1/0230/11.

References

1.Kaul A., Farouki R.T. Computing Minkowski sums of Planar Curves // International Journal of Computational Geometry and Applications. – 1995. – No. 5. – Р. 413–432.

2.Lee I.K., Kim M.S., Elber G. The Minkowski Sum of 2D-Curved Objects // Proceedings of Israel-Korea Bi-National Conference on New Themes in Computerized Geometrical Modeling / Tel-Aviv Univ. – Tel-Aviv, 1998. – P. 155–164.

3.Lee I.K., Kim M.S. Polynomial/Rational Approximation of Minkowski Sum Boundary Curves // Graphical Models and Image Processing. – 1998. – Vol. 60, No. 2. – P. 136–165.

4.Peternel M., Manhart F. The Convolution of Paraboloid and a Parametrized Surface // Journal for Geometry and Graphics. – 2003. – No. 7. – P. 157–171.

5.Velichova D. Minkowski Sum in Geometric Modelling // Proceedings of the 6th Conference «Geometry and Graphics». – Ustroň, 2009. – Р. 65–66.

6.Velichova D. Minkowski Set Operations in Geometric Modelling of Continuous Riemannian Manifolds // Scientific Proceedings 2009. – Bratislava, 2009. – Р. 179–186.

7.Velichova D. Minkowski Set Operations in Modelling of Manifolds // Proceedings of the GeoGra 2012 International Conference. – Budapest, 2012.

МАЛЕНЬКИЕ ХИТРОСТИ КОМПЬЮТЕРНОЙ ГРАФИКИ

Некоторое время назад создано учебное пособие, с миру по ниточке, как собрание хитростей и ловкостей народных для работы в CorelDraw, начиная еще с 3-й версии. Проверено в процессе обучения в течение последних 18 лет. Контингент – от детей дошкольного возраста до пенсионеров.

Основы основ. Представляется разумным прежде, чем чего-либо начать, условиться: что мы собираемся делать, как и зачем. Несколько слов о видах КГ: их логично выделять три. Растровая – мозаика из точек разных оттенков, которую

178

elib.pstu.ru

легко перекрашивать, но трудно повернуть изображение, оставив зерна в мозаике по рядам и колоннам, трудно (а точнее – невозможно) уменьшить изображение, не потеряв четкости, также невозможно увеличить, не добавив лишних точек. Векторная, или командная, – вариант аппликации, в которой у каждого элемента свои параметры – не только размеры и координаты с углами поворота и перекоса, но и цвет или тип заливки, контура, прозрачность и прочие эффекты. Третий вид – трехмерная графика больше относится к моделированию и графикой становится только при прорисовке, в процессе рендеринга (тонирования).

Где и чем. Прежде, чем изменить какой-нибудь объект, необходимо его выделить. Компьютеры пока еще не догадываются, куда наш ясный взгляд направлен да помыслы светлые устремлены. Нечем им пока это ощутить. Хотя такие шутки могут стать чреватыми. Ведь начали же текстовые процессоры контролировать не только орфографию, но, отчасти, даже стилистику.

Итак, выделить объект можно разными способами:

1.Кликнув по нему мышкой, точнее – курсором. Раньше тоже приходилось предупреждать, что для выделения существует специальный инструмент – указатель, стрелочка или инструмент сбора (pick tool). Теперь это можно сделать практически любым инструментом.

2.Хитрость есть и здесь: если объект не имеет заливки, то выделить его можно только за контур. Правда, для начинающих есть настройка «считать все объекты заполненными» (treat all objects as filled), но при ее использовании невозможно взять нижележащие объекты, даже если они видны под пустым.

3.Обтянуть рамкой необходимое количество объектов, но только полностью. Добавить к выделению или убрать из него можно всеми вышеозначенными способами, но с удержанием клавиши Shift.

Узнать, какие объекты удалось выделить, а какие пока нет, очень просто. На них загораются крохотные маячки. Да и в строке состояния (status Line) написано, чего и сколько выделено. А для полной уверенности никто не мешает применить к выделению что-либо яркое, например выкрасить в яркий цвет.

Адля того, чтобы не испортить свое великое творение существует «задний ход», даже три разных:

1.Если все в порядке – просто Ctrl-Z и продолжаем работать.

2.Кто этого еще не запомнил – есть строка меню: Edit\Undo…, причем тут вам еще и напишут, какое именно действие сейчас будет отменено.

3.Но чаще народу не лень наматывать километры бедной мышкой, нажимая на кнопку UnDo стандартной панели ***, хотя и тут большинство не знают, что у этой кнопки и у ее пары – ReDo *** есть целый список отмен и возвратов. *** Но для того, чтоб его увидеть, надо мучительно напрячь память и вспомнить, что делается это ПРАВОЙ клавишей мышки (ПКМ). В общем надежнее зрительно убедиться, что выделено то, что нужно, и ничего лишнего. Потом шаг назад и продолжаем работу. Да и непродолжительная пауза при работе совсем не во вред.

179

elib.pstu.ru

Количество отмен у CorelDRAW может превышать и 100, если обратиться к настройкам, хотя по умолчанию оно чаще равно 20. Смысл здесь в следующем – пока нельзя отменять выборочные действия, а только весь хвост списка. А если пользователь заметил это через 70–80 шагов после ошибки… Остается только сожалеть. Но и тут выход есть. Современные версии уже не сбрасывают буфер откатов при сохранении. Поэтому можно записать результат для дальнейшего использования, а потом попытаться откатиться в глубь времен по череде отмен действий. Может и повезет, упущенный вариант может оказаться все еще в зоне доступа.

Анекоторые пользователи поступают еще хитрее – нужную конфигурацию выделяют и копируют в буфер, затем проходят цепь откатов и в нужном моменте вставляют то, что приготовлено в буфере. Но этот путь чреват зависаниями по причине сложности и громоздкости операций. Поэтому страховочное сохранение никогда не будет лишним. Эта же причина заставляет работать

вавторских вариантах программ, а не в русифицированных, в которых полезного добавлено быть все равно не может, а вот «чудес» прибавляется изрядно – даже инструмент в разных местах одной и той же программы может называться по-разному. Этот же пункт неплохо напомнить и в свете авторского права на программные продукты.

Чего и как. Небольшой экскурс в мелочи интерфейса.

Общие позиции интерфейса здесь особо новинок не несут. С некоторого уровня пользователи начинают подгонять настройки под себя. Простейший способ – правый щелчок на любой панели инструментов, и вы получаете список возможных панелей. Не забывайте, что многие регуляторы появляются только при включении определенных инструментов или выборе конкретных объектов.

Амногие панели оформлены в виде «докеров» и могут сворачиваться или компактно парковаться, организуя нужные пользователю наборы. У многих из них есть еще и горячие клавиши быстрого вызова, например [Alt]/[F7] для

Transform.

Всякие слова… Немного о терминологии.

Некоторые термины стоит оговорить в самом начале, чтобы не разъяснять потом. Левый и правый щелчок мышкой знают уже многие, некоторые даже отличают их от «drag and drop – тяни – бросай». Здесь еще будет применяться ужасная комбинация из мышкиных клавиш – не отпуская левую, щелкнуть правой для оставления оригинала трансформируемого объекта. Около курсора при этом появляется маленький +. Если оригинал оставлять не нужно, повторный правый щелчок отменяет эту команду, опять же не отпуская левой клавиши.

При использовании дополнительных клавиш не забывайте, что опрос клавиатуры происходит с несусветной частотой – несколько сотен раз в секунду. То есть то, что вам кажется ОДНОВРЕМЕННЫМ отпусканием обеих клавиш, на самом деле очень-очень различимые для компьютера события, и только вы не знаете, что происходит раньше. Поэтому отпускаем СНАЧАЛА клавишу команды – букву, цифру, кнопку мышки, и только ПОТОМ – управляющую

(CTRL, ALT, SHIFT или еще какую).

180

elib.pstu.ru