
Математическое моделирование в естественных науках.-1
.pdft |
dε1 |
|
|
|
|
|
|
|
|
|
< 1, |
(3) |
|
εпр (k,θ,ε |
u |
,W ) |
||||
t0 1 |
|
|
|
|
||
где ε1пр – предельная главная деформация, зависящая от коэффициента жесткости напряженного состояния, температуры, скорости деформирования и влажности W; ε1 – накопленная
главная деформация.
Непосредственное использование критерия (3) в практических расчетах предполагает его значительное упрощение:
– не будем учитывать в данной работе зависимость предельной главной деформации ε1пр от температуры, скорости де-
формирования и влажности в силу практического отсутствия исходных данных;
– от интеграла (3) перейдем к конечной зависимости. Таким образом, предлагается использовать упрощенный
вариант критерия (3) в виде
ε1 < ε1пр (k) . |
(4) |
По аналогии с классическими критериями разрушения можно ввести коэффициент запаса прочности по деформационному критерию:
n = |
ε1пр ( p / σu ) |
. |
(5) |
|
ε1 |
||||
|
|
|
||
Вид зависимости ε1пр |
= ε1пр ( p / σu ) , определенный |
путем |
||
численного моделирования экспериментов на сжатие, и коэффициенты критерия разрушения (4) выражаются как
ε1 ≥ ε1пр ( p / σu ) = kМ (0,012k2 + 0,136k + 0,50) при k < 0,
61
ε1 ≥ ε1пр ( p / σu ) = kМ (9,13k3 −1,63k2 + 1,77k + 0,50) при k > 0, (6)
где kМ = 2,1 (для сильвинита);
ε1 ≥ ε1пр ( p / σu ) = kМ (0, 238k2 + 0,41) при k < 0,
(7)
ε1 ≥ ε1пр ( p / σu ) = kМ (−3,92k4 + 11,98k3 + 3,72k2 − 0,84k + 0,41)
при k > 0,
где kМ = 0,35 (для карналлита).
Численное моделирование процесса сжатия образцов соляных пород было проведено в двумерной осесимметричной постановке в пакете Ansys. В расчетной схеме рассматривалась половина образца: левая вертикальная граница – ось симметрии, правая – свободная граница. На нижней грани реализовалось отсутствие перемещений (неподвижная траверса
ссильным трением). На верхней грани отсутствовало радиальное перемещение и задавалось вертикальное перемещение
сшагом εу = −0,1% (подвижная траверса испытательной ма-
шины с сильным трением).
Исходные параметры расчета: модуль Юнга 8500 МПа, коэффициент Пуассона 0,35, масштабный коэффициент kM = 2,1, диаметр образца d = 4 см.
Впластической области принята модель кинематического деформационного упрочнения, использующая экспериментальные кривые нагружения.
Вобласти (элементах сетки) образца, где в ходе нагружения срабатывал критерий разрушения (n<1), свойства трещиноватого материала понижались с коэффициентом уменьшения свойств материала less = 0,5.
62
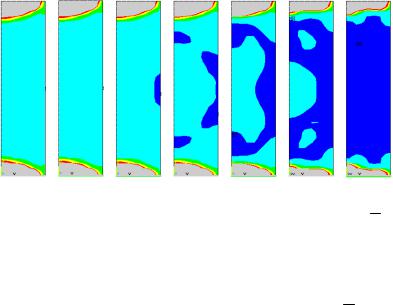
ε y = 3,4% |
3,5% |
3,6% |
3,7% |
3,8% |
3,9% |
4% |
Рис. Поле коэффициента запаса прочности образца сильвинита h = 2 d
(темным цветом показаны области разрушенного материала)
На рисунке, в качестве примера представлены поля коэф-
фициента запаса прочности для образца сильвинита h = 2 , где d
h – высота образца. Цифрами сверху отмечена величина текущей средней вертикальной деформации образца.
Список литературы
1.Пластичность и разрушение / В.Л. Колмогоров, А.А. Богатов, Б.А. Мигачев [и др.]. – М.: Металлургия, 1977. – 336 с.
2.Аптуков В.Н. Деформационный критерий разрушения образцов соляных пород // Физико-технические проблемы разработки полезных ископаемых. – 2016. – № 3. – С. 39–45.
63
ЧИСЛЕННОЕ И АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ЧИСТОГО ИЗГИБА В ПОСТАНОВКЕ ДИЛАТАЦИОННОЙ И ГРАДИЕНТНОЙ ТЕОРИИ ПОРИСТЫХ СРЕД
А.В. Волков, Ю.О. Соляев, С.А. Лурье
Институт прикладной механики Российской академии наук,
Москва, Россия, volkov.9291@mail.ru
Рассмотрены численные и аналитические решения задач чистого изгиба балки в двух различных неклассических моделях пористых сред. В первом случае рассматривается среда с микроструктурой, которая является частным случаем теории Миндлина, в предположении, что в среде присутствуют только свободные деформации изменения объема. Во втором случае рассматривается градиентный вариант теории пористых сред, который получен на основе вариационной формулировки теории сред с микроструктурой с использованием гипотезы Аэро–Кувшинского о пропорциональности свободных и стесненных деформаций изменения объема. Проводится сравнение аналитических решений, построенных полуборатным методом, и численных решений, построенных методом конечных элементов.
Ключевые слова: пористые среды, микродилатация, задача чистого изгиба балки, модели обобщенных континуумов.
Классическая формулировка теории упругости пористых сред (дилатационной теории упругости) предполагает введение параметра изменения объемного содержания материала φ в каче-
стве дополнительной кинематической переменной модели [1]. С точки зрения модели Миндлина в такой среде допускается присутствие только свободных деформаций изменения объема (свободной дилатации). Таким образом, в модели имеются следующие кинематические соотношения:
εij |
= |
1 |
(ui , j +u j ,i ), |
φ = PR − P. |
|
|
2 |
|
|
Здесь ui – поле перемещений, |
εij – тензор деформаций, |
|||
PR – исходное объемное содержание пор, P – текущее объемное содержание пор.
64
Определяющиесоотношениямоделидляизотропнойсреды:
σij = λθ+ 2μεij + βφδij , hi = αφ,i , g = −ξφ− βεkk .
Здесь σij – тензор напряжений, θ = εkk δij – дилатация, λ, μ – параметры Ламе, hi , g – неклассические самоуравновешенные напряжения, β, ξ, α– дополнительные материальные константы
теории пористых сред.
Уравнения равновесия в модели в предположении отсутствия объемной нагрузки:
σij , j = 0 , hi , i + g = 0.
Граничные условия:
σij nj = pi0 , ui = ui0 , hi ni = αφ,i ni = 0.
Градиентный вариант модели сред со свободной дилатацией был предложен в работе [2] путем введения гипотезы Аэро – Кувшинского о пропорциональности свободных и стесненных деформаций изменения объема. В этом случае из кинематических переменных модели исключается перепенная изменения объемного содержания φ, так как она считается линейно-
пропорциональной дилатации среды. Вместо трех материальных констант β, ξ, α в модели возникает единственный масштабный
параметр . Определяющие соотношения модели формулируются для классического тензора напряжений и неклассического вектора напряжений mi (аналог моментных напряжений в градиентной теории упругости):
σij = λεkk δij + 2μεij , |
mi = (λ+ 2μ) 2εkk ,i . |
Уравненияравновесиятеорииимеют повышенныйпорядок:
σij, j − mi, jj = 0.
65
Естественные граничные условия следуют из вариационной постановки:
σij nj − mi, j nj = pi0 , ui = ui0 , |
mj nj = 0. |
В докладе рассматривается решение задачи о чистом изгибе балки. Приближенное аналитическое решение в дилатационной теории упругости впервые было построено в работе [1]. Вдокладе представлено аналогичное аналитическое решения, построенное врамках градиентной теории упругости пористых сред. Представлено сравнение численных и аналитическых решений в дилатационнойтеорииупругости ивградиентнойтеорииупругости.
Список литературы
1.Stephen C. Cowin, Jace W. Nunziato Linear elastic materials with voids // Journal of Elasticity. – 1983. – 13.
2.Белов П.А., Лурье С.А., Континуальная модель микроге-
терогенных сред // ПММ. – 2009. – Т. 73, № 5. – С. 833–848.
МОДЕЛИРОВАНИЕ ПЛОСКОПАРАЛЛЕЛЬНЫХ ТЕЧЕНИЙ МЕТОДОМ РЕШЕТОЧНЫХ УРАВНЕНИЙ БОЛЬЦМАНА
И.В. Володин1, А.А. Алабужев2
1Пермский государственный национальный исследовательский университет,
Пермь, Россия, ivanwolodin@gmail.com
2Институт механики сплошных сред УрО РАН,
Пермь, Россия, alabuzhev@mail.ru
Численно моделируются плоскопараллельные течения методом решёточных уравнений Больцмана (Lattice Boltzman Method, LBM) сиспользованием аппроксимации Батнагара–Гросса–Крука. Рассматриваются двумерные течения Куэтта и Пуазейля, а также течение в прямоугольной полости с подвижной стенкой.
Ключевые слова: метод решеточных уравнений Больцмана, LBE, LBM, изотермическая жидкость, однофазная жидкость, вязкая жидкость.
66

Ввиду того, что течение жидкости описывается сложными дифференциальными уравнениями, которые не имеют общего решения в аналитическом виде, широкое распространение получили различные вычислительные методы. Подход, предложенный в данной статье, базируется на кинетическом уравнении Больцмана. Дискретизация этого уравнения и его дальнейшее программирование стали возможными благодаря аппроксиматическому решению Батнагара–Гросса–Крука [1].
Метод решеточных уравнений Больцмана удобен своей концептуальной и вычислительной простотой, кроме того, он легко распараллеливается.
Уравнение Больцмана имеет вид:
|
x |
f |
(1) |
|
p f |
(1) |
+ |
∂f (1) |
= Г |
(+) |
− Г |
(–) |
, |
v |
|
+ F |
|
∂t |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где v – скорость жидкости; f – одночастичная функция Больцма-
на; F – сила, действующая на жидкость; Г(+) − Г(–) – оператор столкновения.
Для численного моделирования нам необходимо:
♦Ввести равномерную сетку пространственных координат, при этом поведение жидкости будем определять именно
вэтих узлах сетки.
♦Дискретизировать время – будем определять состояние жидкости в равноотстоящие моменты времени.
♦Позволить частицам иметь только определенные значения скорости, так, чтобы за шаг по времени они успевали перейти в соседний узел.
Рассматриваются частицы одинаковой единичной массы, следовательно, устанавливается простая связь с макроскопическими параметрами жидкости [2].
Связь с макроскопической скоростью:
u = 1ρ n fa .
a=1
67
Связь с макроскопической плотностью:
n
ρ = fa ,
a=1
где n – количество разрешенных скоростей. Дискритизированное уравнение Больцмана имеет вид:
|
|
|
|
|
|
fi − fieq |
|
fi (r |
+ ci |
,t + 1) |
= |
fi (r |
,t) − |
|
, |
τ |
|||||||
где τ – время релаксации, время перехода системы из текущего состояния fi в состояние, соответствующее наименьшей энер-
гии, fieq – равновесная функция распределения (в данной работе
используется функция распределения Максвелла [2]).
Для описания движения частицы используется двумерная девятискоростная модель D2Q9 [1, 2].
Вычислительнаяпрограмма состоит изнесколькихмодулей:
1)Задание макроскопических параметров жидкости, таких как плотность, скорость и время релаксации системы.
2)Распространение введенных значений на каждый узел.
3)Задание граничных условий.
4)Вычисление скорости в каждом узле.
5)Задание оператора столкновения и вычисление функции Больцмана на всей решетке.
6)Задание градиента внешней силы.
7)Циклическое повторение пунктов 3–6 до тех пор, пока система находится в неравновесном состоянии.
Рассматриваются двумерные течения Куэтта и Пуазейля,
атакже течение в прямоугольной полости с подвижной стенкой. Для иллюстрации работы метода приведем результаты моделирования задачи течения вязкой жидкости в прямоугольной полости с твердыми стенками, верхняя стенка которой движется с заданной постоянной скоростью: проекция компоненты скоро-
68
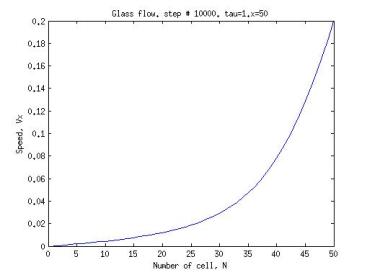
сти на ось Ox – Vx = 0,2, на ось Oy – Vy = 0. Данная задача не имеет точного аналитического решения. Численное решение было получено, например, в работе [3].
Графики решения данной задачи методом LBM (Lattice Boltzman Method) при входных параметрах единичной плотности и единичного времени релаксации приведены ниже. Они соответствуют установившемуся стационарному течению в момент времени t = 10 000. Все физические параметры обезразмерены в единицах вязкости.
Нами была использована решетка Nx × Ny=100 × 50.
Из приведенных графиков (рис. 1, 2) видим, что решение,
полученное с помощью LBM (Lattice Boltzman Method), на ша-
ге по времени, который соответствует установившемуся течению, сошлось к правильному результату (например, в сравне-
нии с [3]).
Рис. 1. Течение в прямоугольной полости. Зависимость Vx от Ny
69
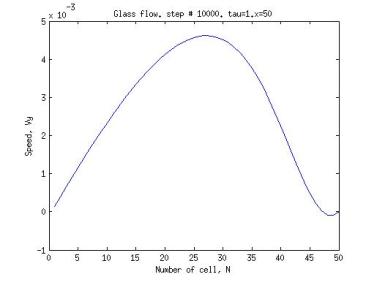
Рис. 2. Течение в прямоугольной полости. Зависимость Vy от Ny
В будущем планируется продолжить работу с LBM и рассмотреть неизотермические задачи с многофазными жидкостями.
Список литературы
1.Sukop M.C., Thorne D.T. // Jr. Lattice Boltzmann Modeling. – Springer-Verlag Berlin Heidelberg, 2006, 2007. – 173 p.
2.Succi S. The Lattice Bolyzman Equation for Fluid Dynamics and Beyond. – Clarendod Press Oxford, 2001. – 299 p.
3.Chen Peng The Lattice Boltzmann Method for Fluid Dynamics: Theory and Applications. – M. Math Department of Mathematics Ecole Polytechnique Federale de Lausanne, 2011. – 134 p.
70
