
Проблема качества графической подготовки студентов в техническом вуз
..pdf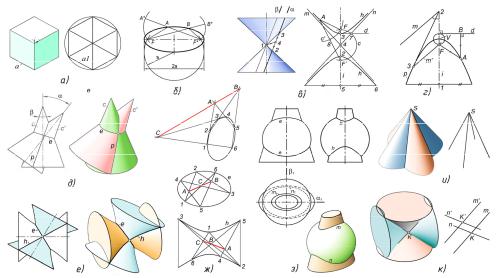
примерах характерных задач из курса НГ, применительно к которым ответ известен качественно или даже количественно.
Нами разработан набор тестов, позволяющий всесторонне проверить графический редактор, часть тестов приведена ниже. Тестирование выполнено в пакете AutoCAD, но результаты могут быть повторены и в других пакетах САПР, применяемых в учебном процессе кафедр графики (SolidWorks, Inventor, Компас). Все построения выполняются с объектными привязками или с применением параметризации [16].
2.1. Изометрия куба
Рассмотрим задачу о проекции куба на плоскость, перпендикулярную одной из его диагоналей (рис. 1, а). Известно, что проекция представляет собой правильный шестиугольник. Вывод был сделан И. Кеплером (1619 г.) и А. Фрезье (1738 г.) [17, 18]. Это ортогональная изометрия. В AutoCAD предусмотрено построение четырех изометрий (по количеству диагоналей куба). Цель данного теста – проверить, насколько изометрия куба, создаваемая в AutoCAD, является правильным шестиугольником.
Рис. 1. Тестирование погрешности компьютерных построений: а – изометрия куба; б – «штатный» эллипс; в, г – коники «штатной» квадрики; д, е – коники в пересечении штатных и нештатных квадрик; ж – тестирование по шестиугольнику Паскаля; з – точность построения проекций линий пересечения; и, к – точность построения прямых при пересечении квадрик
371
Построим куб (команда Box) с произвольной длиной стороны. Построим одну из его ортогональных изометрий. Спроецируем куб (команда Solprof или Flatshot) на плоскость экрана. Зададим точность (Units) до восьмого знака ПЗ. Измерим (List) длины всех 12 отрезков, являющихся проекциями ребер куба. Сравнив между собой полученные значения, убедимся, что длины совпадают до последнего знака. При длине стороны куба 100 все они равны 81,64965809. Это первая (качественная) проверка. Для второй (количественной) проверки вычислим длину каждого из отрезков. На основе тригонометрических преобразований, вероятно, повторяя выкладки Фрезье, получим, что для куба со стороной a длина отрезков изометрической проекции определяется формулой a1 = asin (arctg (sqrt2)). При а = 100 получим то же значение, что и при измерении графически построенной проекции, равное 81,64965809. Вы-
вод: компьютер выполняет построение изометрии 3D-объектов с погрешностью 10–8.
2.2.Точность построения коник
Вучебном процессе коники выступают как сечения и линии пересечения квадрик, проекции этих линий, очерковые образующие квадрик. Рассмотрим точность коник согласно их определению как сечений конуса плоскостью.
ВAutoCAD существуют три «штатные» квадрики, являющиеся примитивами AutoCAD: конус, сфера, цилиндр. Для остальных «нештат-
ных» квадрик отсутствуют специальные команды построения. Это гиперболоиды, параболоиды, эллипсоиды, их нужно создавать вращением или перемещением коник.
То же относится и коникам. Штатные коники– эллипс, окружность. Для них предусмотрены специальные команды построения. Эти коники диагностируются качественно, т.е. при наведении курсора выводится имя коники. Гипербола и парабола– «нештатные» коники. В AutoCAD их получают каксечения конуса, этиобъектыформируютсякаксплайн-кривые.
Оценим точность, с которой создаются «штатные» коники – эллипсы (рис. 1, б). Для этого проверим выполнение его определяющего свойства: эллипс как геометрическое множество точек (ГМТ), сумма расстояний которых до точек фокуса является постоянной. Строим произвольный эллипс e. С помощью окружности находим точки фокусов F и F*. Назначаем две произвольные точки эллипса A, B. Соединяем их отрезками с точками фокусов. Строим отрезки F*A* и FB*, длины кото-
372
рых равны сумме расстояний от точек A, B до фокусов. Измерениями убеждаемся, что длины совпадают до восьмого знака ПЗ. Это указывает, что эллипс иокружность воспроизводятсяспогрешностьюнеболее10–8.
Для оценки точности «нештатных» коник построим гиперболу h (рис. 1, в) как сечение кругового конуса плоскостью α. Для построения асимптот гиперболы n, m построим сечение β||α и переместим его в плоскость α в центр гиперболы: 1→ 4. В плоскости α строим ось гиперболы i (4–5), отрезок d, пепендикулярный i, находим точку 7, с помощью окружности c находим фокусы гиперболы F, F ′.
Точность гиперболы определим, учитывая, что она является ГМТ, для которых разность расстояний до точек фокуса является постоянной, равной расстоянию между вершинами гиперболы, точки 2, 3. Задаем произвольную точку A гиперболы h, строим отрезок AF ′, с помощью окружности c′ определяем точку 8 = c′∩AF′. Измерив длины отрезков (2, 3) и (8, F′), убеждаемся, что они равны с точностью до восьмого знака ПЗ.
Параболу p (рис. 1, г) также строим как сечение кругового конуса плоскостью. По средней точке параболы находим ее вершину V. Строим ось параболы i (1–V). Для нахождения фокуса F реализуем оптические свойства параболы. Из произвольной точки 2 оси i строим отрезок (2, 3), касательный к параболе. Точку 3 касания определяем объектной привязкой. Строим отрезок m, симметричный i относительно (2, 3), и отрезок m′ ||m. Находим фокус параболы F = m′ ∩ i и директрису d.
Точность параболы оцениваем исходя из ее определения как ГМТ, равноудаленных от фокуса и директрисы. Назначаем произвольную точку А параболы. Строим отрезки AF и AB и измеряем их длину. Убеждаемся, что длины совпадают до восьмого знака ПЗ.
Гипербола и парабола как сечения квадрик и как объекты AutoCAD представляют собой плоские сплайны. Эту характеристику (Properties: Planar) можно прочесть по команде List. Приведенным тестированием
показано, что погрешность построения таких сплайнов находится на уровне 10–8.
2.3. Точность построения линий пересечения
Приведем примеры тестирования, основанные на оценке точности коник, образующихся в частных случаях пересечения квадрик [19]. При тестировании важно обеспечить точность реализации частного случая. Например (рис. 1, д), построить круговой конус, создать его дубликат и повернуть вокруг произвольной точки оси. Реализуется теорема Мон-
373
жа. В зависимости от значений угла α в пересечении конусов образуются эллипсы, параболы, гиперболы в различном сочетании. В приведенном примере возникли эллипс и парабола.
Необходимо различать взаимное пересечение «штатных» квадрик
ипересечение, в котором хотя бы одна квадрика «нештатная». В первом случае образуются «штатные» коники (эллипс, окружности) и плоские сплайны (гипербола, парабола). «Штатные» коники диагностируются
качественно. Их погрешность, как показано выше, находится на уровне 10–8. Погрешность гипербол и парабол была проверена приведенными выше методами (см. рис. 1, б, в). Она составляет 10–5–10–8.
При пересечении «нештатных» квадрик коники реализуются как неплоские сплайны (Non-Planar). Примером (рис. 1, е) является пересечение двух однополостных гиперболоидов вращения (ОГВ), имеющих общую вписанную сферу. Очерковую гиперболу ОГВ получим как сечение кругового конуса, сам ОГВ – ее вращением вокруг мнимой оси. Модель пересечения получим поворотом дубликата гиперболоида вокруг некоторой точки его оси, желательно точки центра очерковой гиперболы. В приведенном примере в пересечении возникли эллипс
игипербола (рис. 1, ж).
Для исследования линию пересечения копируем. Установим плоскость построений по трем каким-либо точкам сплайна. Командой List выводим координаты остальных точек и по z-координате определяем их отклонение от плоскости. Депланация не превышает 10–4. Последующая проверка коник, выполненная по методам (см. рис. 1, б–г), показывает погрешность на уровне 10–4–10–6.
2.4. Оценка коник на основе теоремы Паскаля
Теорема Паскаля (1623–1662) – одна из основных теорем проективной геометрии [20]. Применим ее для оценки точности коник как линий пересечения. На тестируемой конике зададим шесть произвольных точек и произвольно их пронумеруем 1–6 (рис. 1, ж). Соединим точки отрезками прямых (Line) по порядку принятой нумерации, т.е. в последовательности 1–2–3–4–5–6–1. Последний отрезок 6–1 замыкает ломаную линию, образуя шестиугольник Паскаля. Для каждого варианта нумерации образуется свой шестиугольник. При простановке точек их расположение не должно быть симметричным. Находим три точки пересечения следующих пар отрезков: А = (1–2) ∩ (4–5); B = (2–3) ∩ (5–6); C = (3–4) ∩ (6–1). Указанные точки могут находиться как на пересечении отрезков, так и на их продолжении.
374
Согласно теореме Паскаля, если линия является коникой, то точки A, B, C принадлежат одной прямой. Для проверки этого положения задаем (Units) предельную точность измерения углов, т.е. до восьмого знака ПЗ. Устанавливаем плоскость измерений в плоскость тестируемой коники. Определяем (List) угол между отрезками AC и BC (угол Паскаля). Предварительно рекомендуем тестировать какой-либо «штатный» эллипс и убедиться, что для него измеряемый угол с предельной точностью равен 0 или 180°.
Угол Паскаля весьма чувствителен к отклонению формы кривой от коники. Так, смещение осей ОГВ в примере (см. рис. 1, е) на 1 %, т.е. отклонение от теоремы Монжа, приводит к увеличению угла Паскаля в 1000 раз. Проведенный эксперимент и другие, аналогичные ему, позволили считать величину 10–3 градуса как граничное значение угла Паскаля. При меньших значениях этого угла проверяемая линия уверенно может рассматриваться как коника.
В рассмотренных нами примерах угол Паскаля не превысил 10–5, что указывает на высокую точность компьютерных построений. Например, для гиперболы (см. рис. 1, ж), возникшей при пересечении гиперболоидов (см. рис. 1, е), угол составил 10–5–10–6 градусов в зависимости от расположения и нумерации вершин шестиугольника Паскаля.
2.5. Точность проецирования линий пересечения
Известно, что при наличии общей плоскости симметрии квадрик линия их пересечения на эту плоскость проецируется в конику [19]. Воспользуемся этим свойством для оценки точности построения линии пересечения и ее проецирования.
Тестирование выполнено на примере пересечения эллиптического конуса и сферы (рис. 1, з), которые являются «штатными» квадриками. Положение квадрик характеризуется фронтальной α и профильной β плоскостями симметрии. Линия пересечения – пространственная кривая 4-го порядка, содержащая ветви m, n. Ее фронтальной проекцией является эллипс e, профильной – гипербола h. Как объекты AutoCAD эти линии представляют собой плоские сплайны.
Оценка точности компьютерных построений была выполнена по шестиугольнику Паскаля. Для эллипса угол Паскаля составил 0,00002338°, для гиперболы – 0,00005650°, что указывает на высокую точность построений.
Отсутствие горизонтальной плоскости симметрии квадрик приводит к тому, что кривые m1, n1 горизонтальной проекции линии пересе-
375
чения существенно отличаются от эллипса, несмотря на кажущееся с ним сходство. Угол Паскаля для этих кривых составил соответственно 0,031907 и 0,033258, т.е. в 10 раз превысил указанный выше пороговый уровень.
2.6. Прямые линии в пересечении квадрик
При распадении линии пересечения квадрик возможно образование прямых линий в пересечении [19]. Предельным случаем является распадение на четыре прямые. Рассмотрим два примера такого распадения и оценим точность компьютерных построений по точности образующихся прямых.
Четыре отрезка прямых образуются при пересечении двух эллиптических конусов с общей вершиной (рис. 1, и). Построим конусы как «штатные» квадрики, объединим их и извлечем линии пересечения. Диагностирование (List) показывает, что это объекты Line, т.е. предельно точно построенные отрезки прямых линий. Погрешность их по-
строения, как и для всех качественно диагностируемых объектов, находится на уровне 10–8.
Второй пример – пересечение по четырем прямым двух «нештатных» квадрик – ОГВ (рис. 1, к). Для возникновения прямых линий оси гиперболоидов должны пересекаться, очерковые гиперболы и угол между осями гиперболоидов должны быть прямыми. Образуются две пары пересекающихся отрезков прямых: m∩n и m'∩n', причем m||m', n||n'. Командой List определяем, что прямые созданы как сплайны. Установив ПСК осью Х вдоль любого из полученных отрезков, в диагностическом
сообщении видим, что отклонение сплайнов от прямой наблюдается на уровне 10–7.
Таким образом, прямые линии, возникающие при пересечении «штатных» квадрик, создаются с погрешностью на уровне 10–8. При «нештатных» квадриках в качестве прямых образуются сплайны, воспроизводящие прямые линии с точностью 10–7–10–8.
2.7. Дополнительные данные по тестированию компьютерной точности
Приведенные выше тесты легко воспроизвести и убедиться в приведенных нами оценках точности компьютерных построений. Дополнительно отметим наши работы, в которых рассмотрены более сложные частные случаи пересечения квадрик: гиперболоидов с параболоидами
376
[21], софокусных и псевдософокусных квадрик [14]. Рассмотрена оценка точности частных случаев пересечения торов – образование кругов Вилларсо и коник в проекции пересекающихся торов с общей экваториальной плоскостью [22]. Во всех примерах показано, что погрешность построений не выше 10–4.
Для поверхностей, получаемых сдвигом контура по траектории (Sweep), погрешность была исследована при построении геометрически точных моделей резьбы, зубчатых и червячных передач, а также червячной фрезы [16]. Показано, что их погрешность не превышает 10–4.
Для наиболее сложных поверхностей, создаваемых «натягиванием» сплайна на каркас (Loft), погрешность зависит от плотности и точности каркаса. Характерная зависимость погрешности от плотности рассмотрена в работе [23].
3.О негативной роли циркуля и линейки
вучебном процессе
Методы 3D активно внедряются в практику, делая ненужными 2D проекционные преобразования и НГ как их теоретическую основу. Ввиду эффективности 3D-методов сложные задачи курса НГ являются простыми и даже элементарными для новых методов [24, 25]. Покажем, что стремление ограничить алгоритмы геометрического моделирования применением циркуля и линейки с целью достижения геометрической точности негативно влияет на учебный процесс, сдерживая его развитие.
Рассмотрим знаменитую историческую задачу П. Ферма о сферах (1640 г.): построить сферу, касательную к четырем заданным сферам S1 – S4 (рис. 2, а). Решение приведем обзорно. Подробное изложение и наша реализация основных алгоритмов этой задачи переданы к публикации.
3.1. Геометрическая модель задачи Ферма о сферах
Возможны два варианта касания двух сфер: внешнее – сферы расположены снаружи относительно друг друга и внутреннее, при котором одна из сфер расположена внутри другой. Из этого следует, что максимальное количество решений задачи Ферма равно количеству комбинаций из четырех элементов, каждый из которых может иметь два значения, т.е. 4 = 16. В зависимости от положения сфер часть решений может отсутствовать или задача может не иметь решения.
377
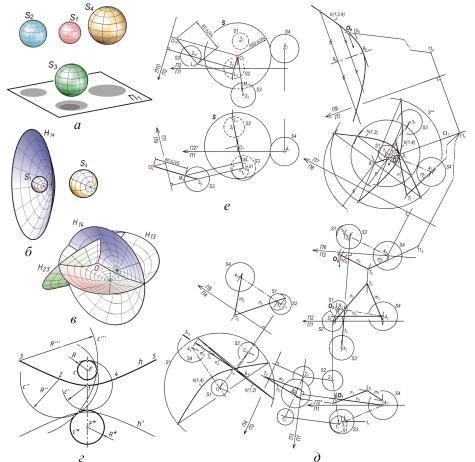
Рис. 2. Задача Ферма: а – заданные сферы; б – гиперболоид как ГМТ, равноудаленных от двух сфер; в – центр искомой сферы; г – построение гипербол; д, е – алгоритм НГ задачи Ферма
За основу нашего решения возьмем алгоритм [26, с. 97; 27] и покажем его реализацию различными компьютерными методами: компьютерными циркулем и линейкой как методом НГ, 3D-методами и 3D-пара- метризацией.
ГМТ, равноудаленных от двух сфер, является одна из чаш двуполостного гиперболоида вращения (ДГВ) (рис. 2, б). Из четырех сфер можно составить шесть пар. Экспериментально установлено, что шесть чаш ДГВ пересекаются в одной точке, которая и является центром искомой касательной сферы (теоретическое обоснование этого вывода нам неизвестно). Поэтому для решения достаточно построить чаши ДГВ трех произвольно выбранных пар сфер и найти их общую точку (рис. 2, в).
378
Составим три пары сфер. Для метода НГ (см. ниже) необходимо, чтобы в каждой паре была общая сфера. Это приведет к софокусному пересечению ДГВ и связанному с этим существенному упрощению решения, поскольку в пересечении образуются коники [14, 26]. Для метода 3D подбор пар не имеет значения.
Для каждой пары сфер решаем планиметрическую задачу по определению гиперболы как очерка ДГВ (рис. 2, г). Строим окружности с, с* сечений сфер выбранной пары некоторой единой плоскостью. В ней найдем ГМТ, равноудаленных от этих окружностей. Точки этого множества можно построить как центры окружностей различного радиуса, касательных к с, с*. Необходимо учесть условие касания искомой сферы с заданными. В приведенном примере ветвь h гиперболы получена при внутреннем касании со сферой, имеющей сечением окружность с, и внешнем касании – с окружностью с*. Ветвь той же гиперболы h′ соответствует противоположным условиям касания, т.е. внешнемукасаниюсокружностью c и внутреннему– с окружностью с*. Центры окружностей, точки F, F*, являются точками фокусов найденной гиперболы h, h′.
Для точного построения гиперболы достаточно найти пять ее точек (например, точки 1–5). Затем по ним построить сплайн-кривую, применив Lisp-программу [28] или параметризацию [16]. Такая гипербола формируется «выходом в пространство» как результат сечения «штатного» конуса и обладает погрешностью 10–8. Построение сплайнкривой вручную, даже по 10–15 точкам, приводит к значительному увеличению погрешности – до 10–2–10–3.
3.2. Алгоритм НГ
Решение, приведенное авторами алгоритма [26] крайне ненаглядно и громоздко. Рассмотрим наше решение, которое также является весьма громоздким, но выполнено оно в соответствии с программой курса НГ.
Составим две тройки сфер. Первая S1, S2, S4, вторая S1, S3, S4. В первой тройке рассмотрим два ДГВ: для сфер S1, S2 и для сфер S1, S4. Наличие общей сферы S1 приводит к тому, что эти ДГВ являются софокусными и пересекаются по гиперболе h (1, 2, 4). Параметры в обозначениях гипербол и ДГВ обозначают номера сфер, для которых они построены. ДГВ второй тройки, имеющей ту же общую сферу S1, пересекаются по гиперболе h (1, 3, 4). Центр искомой общей касательной сферы S – точку O – определяем как точку пересечения гиперболы h (1, 3, 4)
379
и плоскости , в которой расположена гипербола h (1, 2, 4). Саму гиперболу h (1, 2, 4) строить не будем, найдем лишь ее три точки.
Уточним условия задачи. Пусть искомая сфера S имеет внутреннее касание с S1, S2 (т.е. эти сферы расположены внутри S) и внешнее – со сферами S3, S4.
Строим фронтальную и горизонтальную проекции заданных сфер (рис. 2, д). Находим плоскость . Для этого преобразуем чертеж так, чтобы плоскость центров первой тройки сфер стала плоскостью уровня П4. В ней строим софокусные гиперболы h (1, 2) и h (1, 4) как очерковые для ДГВ этой тройки. Из-за перегруженности чертежа построение этих гипербол не показано, оно выполнено по алгоритму (см. рис. 2, г). На пересечении гипербол h (1, 2) и h (1, 4) находим точку 54. С помощью концентрической сферы S* с центром в точке 14 определяем точку 64. По точкам 5, 6 определяем плоскость , перпендикулярную П4, задаем ее двумя отрезками m∩n, которые назначаем в плоскости П5|| с учетом наглядности последующих построений.
Для второй тройки сфер чертеж преобразуем так, чтобы плоскость центров ее сфер стала плоскостью уровня П7. В этой плоскости строим софокусные гиперболы h (1, 3) и повторно – гиперболу h (1, 4). Указанные гиперболы являются очерковыми для ДГВ второй тройки сфер. По точкам 87, 97 определяем плоскость Ω, перпендикулярную П7. В плоскости П8||Ω способом концентрических сфер с центром в т. 17 строим гиперболу h (1, 3, 4).
Последовательным преобразованием из П5 находим проекции отрезков m, n в плоскости П7. Находим точки 10, 11 отрезка, по которому пересекаются плоскости (m, n) и Ω. В плоскости П8 находим точку О пересечения отрезка (10, 11) с гиперболой h (1, 3, 4). Она является центром искомой касательной сферы S. Обратным преобразованием находим ее фронтальную О2 и горизонтальную проекции О1.
Радиус искомой сферы определяем как истинную величину отрезков, соединяющих точку О с центрами заданных сфер, с добавлением или вычитанием радиусов этих сфер в зависимости от условий касания. Например (рис. 2, е), в плоскости П10 для сферы S2, имеющей внутреннее касание, к истинной величине отрезка (O, 2), добавляем радиус сферы S2. Точка L является точкой ее касания с искомой сферой. Для сферы S3, имеющей внешнее касание, определена точка касания М.
380
