Методология научных исследований в сварке

Рис. 7.3

Модули шкал на осях координат приняты равные. Все прямые полученного семейства по z пересекаются в начале координат. Отметим штрихами точки пересечения этих прямых с вертикалью, проведенной через штрих с пометкой 10 шкалы для переменной х. Против всех штрихов напишем значения параметров, которым отвечают наклонные линии – и получим шкалу третьей переменной z. Она оказалась равномерной, так как z входит в уравнение в первой степени. Если бы переменная z была в квадрате, то шкала оказалась бы квадратичной и т.д.

Если семейство прямых, полученное при построении уравнений с тремя переменными, состоит из параллельных линий, то построение шкалы для третьей переменной производится в следующей последовательности. Через последний штрих горизонтальной шкалы проводят вертикаль, затем все параллельные прямые семей-

121

ства продолжают до пересечения с этой вертикалью и у точек пересечения проводят штрихи, для которых пишут соответствующие значения пометок параметра. Расстояние между штрихами с пометками делят на более мелкие деления.

Рис. 7.4

Во все остальных случаях при построении уравнений с тремя переменными нельзя построить шкалу для переменной, принятой за параметр. Точка, отвечающая промежуточному значению параметра, определяется на глаз, что уменьшает точность определения по номограмме, в этом случае рекомендуется строить возможно большее количество линий для третьей переменной.

Для тех уравнений с тремя переменными, которые могут быть представлены в виде y = f(x) (z), объем вычислительных работ для построения номограмм может быть значительно сокращен. В этом случае заданное уравнение разбивают на два путем введения вспомогательной переменной t, и тогда получим: t = f(x), y = t (z).

122

Сперва строят уравнение t = f(x) с двумя переменными, для чего на одной оси координат строят шкалу для переменной х, а на второй оси для вспомогательной переменной. Затем, используя другую систему координат, строят на ней уравнение y = t (z) с тремя переменными, приняв переменную z за параметр уравнения. При этом на одной оси координат строят шкалу для той же вспомогательной переменной t с тем модулем, с каким такая шкала построена на первой системе координат, а на второй оси координат строят шкалу для искомой переменной y. На следующем этапе сопрягают обе системы координат так, чтобы совпали начала координат и оси со шкалами вспомогательной переменной t.

Такое построение номограммы называется построением в двух квадрантах. Если оси вспомогательной переменной t на обеих системах координат вертикальны, то такое сопряжение называется горизонтальным, а если оси горизонтальны, то сопряжение будет вертикальным.

На рис. 7.5 приведена сопряженная номограмма уравнения y 0,2x2 z, построенная в двух сопряженных квадрантах для х от

0 до 10 и для z от 0 до 25.

На обычной сетчатой номограмме заданное уравнение изобразится семейством кривых независимо от того, какую из переменных, x или z, принять за параметр, а потому целесообразнее построить это уравнение в двух сопряженных квадрантах. Заданное уравнение было разбито на следующие два уравнения:

Вверхнем квадранте построено уравнение двух переменных,

внижнем уравнение трех переменных. Очевидно, что построение номограммы заданного уравнения в сопряженных квадрантах проще и точнее, чем построение на обычной номограмме, так как пришлось строить только одну кривую (параболу). Во втором квадранте семейство по z состоит из прямых, пересекающихся в начале координат, поэтому для этой переменной дана своя шкала. Она

123

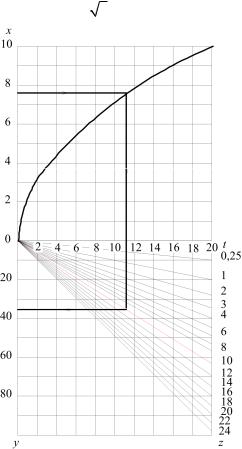
оказалась шкалой квадратных корней, так как переменная z входит в заданное уравнение в виде z .

Рис. 7.5

Рассмотрим пример пользования построенной номограммой. Дано: x = 7,6 и z = 10. Через деление с пометкой 7,6 на вертикальной оси проводим горизонталь до пересечения с параболой, а из полученной точки проводим горизонталь до пересечения с осью y, по шкале которой найдем, что y = 36. Вычислением получаем y = 36,5.

124

7.6.2. Уравнения со многими переменными

Построение номограмм для уравнения со многими переменными – задача сложная и не всегда разрешимая.

Сетчатые номограммы с равномерными шкалами по осям координат для уравнений со многими переменными могут быть построены для уравнений, имеющих вид

y = a f(x) (z) (v) (u).

Такие уравнения называются уравнениями с раздельной функциональной зависимостью переменных. В них функция каждой переменной входит в уравнение самостоятельным множителем. Построение номограмм для уравнения производится путем введения в заданное уравнение вспомогательных переменных и разбивке его на несколько отдельных уравнений. Введем три вспомогательные переменные t, s и p и разобьем уравнение на следующие четыре отдельных уравнения:

t = af(x), s = t (z), p = s (u), y = p (v).

Для построения этих четырех уравнений потребуется четыре сопряженных квадранта. Схема номограммы приведена на рис. 7.6. В первом квадранте (верхнем правом) изобразится уравнение двух переменных, для чего на его внешней вертикали строим шкалу переменной х, а на горизонтальной оси – шкалу вспомогательной переменной t. Уравнение изобразится прямой или кривой линией.

Во втором квадранте (нижнем правом) строим уравнение s = t (z), приняв переменную z за параметр, причем на вертикальной оси строим шкалу для второй вспомогательной переменной s и используем горизонтальную шкалу вспомогательной переменной t. Уравнение изобразится семейством прямых линий, пересекающихся в начале координат.

В третьем квадранте (нижний левый) строим уравнение p = s (u), приняв переменную u за параметр. При этом на горизонтальной оси строим шкалу для третьей вспомогательной переменной p и используем вертикальную шкалу вспомогательной пере-

125

менной s. Уравнение изобразится также семейством прямых линий, пересекающихся в начале координат.

Рис. 7.6

В четвертом квадранте (верхний левый) строим уравнение y = p (v), приняв переменную v за параметр, причем на внешней вертикали квадранта строим шкалу для искомой переменной y и используем горизонтальную шкалу вспомогательной переменной р.

Стрелками показан ход решения (см. рис. 7.6). Шкалы вспомогательных величин при построении хода решений не нужны, поэтому в окончательном варианте номограммы их обычно не вычерчивают.

К достоинствам описанного типа номограмм из сопряженных квадрантов следует отнести:

возможность строить кривые обычно только в первом квадранте, в остальных квадрантах все построенные линии сходящие-

126

ся в начале координат прямые, что значительно упрощает как вычисления, так и построение номограмм;

простоту и наглядность хода решения, что особенно ценно для расчетов, выполняемых методом подбора.

7.7. Сетчатые номограммы с логарифмическими шкалами

7.7.1. Логарифмические координаты

При построении уравнения с двумя переменными в прямоугольных координатах с применением равномерных шкал равных модулей по осям координат весьма часто сталкиваются с тем, что пределы изменения одной переменной значительно больше пределов изменения второй. Рассмотрим, какие неудобства могут возникнуть в таких случаях.

Например, требуется построить номограмму уравнения y = x3 + 2x,

при этом значения переменной х изменяются от 1 до 10. Соответственно значения переменной y: при х = 1 имеем y = 3; при x = 10

имеем y = 1020 (рис. 7.7, а).

Если модуль равномерных шкал переменных = 10 мм, то длина шкалы переменной х – lx = 10 10 = 100 мм, а переменной y – соответственно ly = 10 1020 = 10 200 мм. Очевидно, что построить номограмму такого размера не представляется возможным. В таких случаях приходится модуль равномерной шкалы для переменной, изменяющейся в больших пределах, выбирать значительно меньших размеров.

Предположим, что надо построить номограмму приведенного уравнения размером не более 20 60 мм. Очевидно, что потребуется принять модуль шкалы переменной х как х = 2 мм, тогда lx = 2 10 = 20 мм, а модуль шкалы переменной y как y = 0,06 мм,

тогда ly = 0,06 1020 = 51 мм.

Построенная номограмма уравнения y = x3 + 2x со шкалами переменных x и y указанных длин представлена на рис. 7.7, б.

127

Рис. 7.7

Соотношение модулей обеих шкал 2:0,06 = 33,3 весьма велико, поэтому построенная кривая оказалась значительно искаженной. Кроме того, относительные погрешности отсчетов в разных местах шкалы y будут изменяться в столь больших пределах, что практическое использование номограммы затруднительно.

В целях устранения указанного недостатка можно для переменной, изменяющейся в значительных пределах, откладывать по оси координат не значения переменной, а значения логарифмов переменной. Такую координату точки будем называть логарифмической координатой.

Выполним построение номограммы приведенного выше уравнения y = x3 + 2x в логарифмических координатах, сохранив примерно те же размеры номограммы. Модуль равномерной шкалы для переменной х выбираем так же, как и раньше: x = 2 мм, lx = 2 10 мм.

Модуль для построения логарифмических координат переменной y примем за н = 20 мм. Это позволяет определять значение ко-

128

ординаты lgy с точностью одного десятичного знака мантиссы. Длина предельной логарифмической координаты y записывается как ly = 20 lg1020 = 20 3,01 = 60 мм. Построение уравнения проведем по точкам со следующими координатами:

По оси y откладывались логарифмы чисел, следовательно, относительная погрешность отсчетов по всей оси y будет одинакова. Для определения по номограмме значений переменной y по заданной переменной х надо через точку, отвечающую заданному значению х, на ее шкале провести вертикаль до пересечения с кривой, аиз полученной точки провести горизонталь до пересечения с осью y, где и найдем значениеlg(y). После потенцированиянайдем значение y.

Если в заданном уравнении переменная х также изменяется в значительных пределах, то можно и по оси х откладывать значения lg(x), а не значения переменной х.

7.7.2. Построение логарифмических сеток

Построение номограмм с использованием логарифмических координат требует значительных затрат времени на их вычисление. Этого легко избежать, если на осях координат строить логарифмические шкалы, так как нахождение на логарифмической шкале точки, отвечающей значению переменной, равносильно вычислению логарифма переменной.

Если на одной оси координат построена логарифмическая шкала, а на другой – равномерная и через все штрихи шкал проведены прямые, параллельные осям координат, то получим сетку, ко-

торая называется полулогарифмической.

129

Если на обеих осях прямоугольной системы координат построены логарифмические шкалы равных модулей и через все штрихи горизонтальной шкалы проведены вертикали, а через все штрихи вертикальной оси проведены горизонтали, то полученная сетка называется логарифмической.

Размеры логарифмической сетки зависят от модуля логарифмической шкалы, которую строят на осях координат, и от пределов изменения переменных, так как последние определяют число требуемых модулей каждой логарифмической шкалы.

Построив на осях координат логарифмические шкалы длиной в один модуль, получим логарифмическую сетку (рис. 7.8).

Рис. 7.8

Такая сетка может быть применена, когда пределы значений каждой величины изменяются меньше чем в десять раз, и следовательно, укладываются между значениями 10n и 10т+1. Если же пределы изменения одной или двух переменных не укладываются между 10n и 10n+1, то на осях координат приходится соответственно увеличить число откладываемых модулей логарифмических шкал.

130