
Оптимизация в среде MATLAB
..pdf2. БЕЗУСЛОВНАЯ МИНИМИЗАЦИЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Для поиска минимума нелинейной функции многих переменных при отсутствии ограничений можно использовать функции fminunc
или fminsearch из пакета Toolbox Optimization. Рассмотрим ка-
ждую из них в отдельности.
Предварительно заметим, что в MATLAB принято разделять алгоритмы оптимизации на алгоритмы для задач большой (Large Scale) и средней размерности (Medium Scale), причем это сделано довольно условно. Основное отличие в том, что Large Scale учитывает разреженность матрицы и для ее хранения и операций с ней использует алгебру разреженных матриц. Алгоритмы Medium Scale имеют дело с полными матрицами и оперируют соответствующей алгеброй. При большой размерности задачи это требует много памяти и времени. Рекомендуется сначала выбирать Medium Scale, так как эти алгоритмы имеют более широкие функциональные возможности.
2.1. Функция fminunc
По умолчанию функция fminunc настроена на алгоритм Large Scale. Он базируется на методе доверительных областей (Trustregion method), т.е. последовательной аппроксимации целевой функции в окрестности текущей точки более простой функцией, по которой находят следующее приближение к минимуму исходной функции. Алгоритм Large Scale требует задания градиента целевой функции, иначе fminunc будет использовать Medium Scale. Чтобы явно указать Medium Scale, следует в качестве аргумента функции optimset записать 'largescale','off'.
В алгоритме Medium Scale можно выбрать один из трех методов: квази-ньютоновкий метод BFGS (Бройдена – Флетчера – Голдфарба – Шэнно) или DFP (Дэвидона – Флетчера – Пауэлла) и метод наискорейшего спуска (steepest descent method). По умолчанию используется метод BFGS, а для указания другого метода в опции нужно добавить параметр 'HessUpdate' со значением 'dfp' или 'steepdesc'.
Большинство параметров являются общими для Large Scale и Medium Scale, но часть присуща только одному из них. Все параметры с краткими пояснениями и значениями по умолчанию приведены в прил. 1.
11
Варианты обращения к функции fminunc:
x = fminunc(fun,x0)
x = fminunc(fun,x0,options) x = fminunc(problem) [x,fval] = fminunc(...)
[x,fval,exitflag] = fminunc(...) [x,fval,exitflag,output] = fminunc(...) [x,fval,exitflag,output,grad] = fminunc(...) [x,fval,exitflag,output,grad,hessian] =fminunc(...)
Смысл обозначений выходных аргументов:
x и fval – вектор значений искомых переменных и значение целевой функции;
exitflag – указывает причину завершения алгоритма, может принимать следующие значения:
1 – величина градиента меньше заданной точности TolFun,
2 – изменения X меньше заданной точности TolX,
3 – изменения f меньше заданной точности TolFun,
5 – предсказанное уменьшение f меньше чем TolFun,
0 – превышено максимальное число итераций или число вычислений f,
–1 – алгоритм завершен функцией вывода (решение не получено); Grad – градиент целевой функции;
Hessian – гессиан целевой функции;
Output – структура, содержащая информацию о процессе в следующих полях:
Iterations – число итераций, funcCount – значение целевой функции,
firstorderopt – условие оптимальности 1-го порядка, algorithm – использованный алгоритм,
cgiterations – общее число итераций (для алгоритма большой размерности),
stepsize – заключительное смещение по X (для алгоритмов средней размерности),
message – сообщение о завершении.
12
Входные аргументы:
fun – либо только целевая функция, либо функция, возвращающая значения целевой функции и ее градиента, либо функция, возвращающая значения целевой функции, ее градиента и гессиана; в первом случае она может задаваться, как показано в гл. 1, а во втором случае – m-файлом с двумя выходными аргументами f и g, причем градиент g – векторный аргумент (элементы разделяются точкой с запятой). Пример:
function [f,g] = myfun1(x) f = 2*x(1)^2+x(2)*x(1)+x(2)^3;
g=[4*x(1)+x(2);x(1)+3*x(2)^2];
втретьем случае – также m-файлом с тремя выходными аргументами:
function [f,g,H] = myfun2(x) f = ...;
g = ...; H = ...;,
где H – матрица вторых производных целевой функции.
Чтобы аналитические выражения градиента и гессиана использовались в алгоритме, их необходимо включить в options:
options=optimset('GradObj','on')
или options=optimset('GradObj','on',’Hessian’,’on’).
В противном случае они будут вычисляться приближенно через конечные разности;
x0 – начальная точка, задается пользователем;
options – используется для внесения изменений в настройки параметров процесса;
problem – задает задачу указанием objective – целевая функция, x0 – начальная точка,
solver –'fminunc'
options – настройки параметров.
Следует иметь в виду, что в MATLAB выходные аргументы, как и входные, могут указываться только в том порядке, который предписан синтаксисом обращения к функции минимизации. Так, например, при обращении к fminunc недопустима запись
[x,fval,output] = fminunc(...)
из-за пропуска аргумента exitflag.
13
Пример 2.
Найти минимум функции Розенброка f(X)=100( x2 – x12 )2 + ( x1 –1)2.
Эта функция часто используется в качестве тестовой при сравнении эффективности разных алгоритмов, так как имеет сильно выраженную овражную структуру. Она достигает минимума в точке (1; 1).
Программу запишем в виде функции runfminunc с вложенной функциейoutfun, обеспечивающей вывод x и fval на каждой итерации:
function history = runfminunc(x0)
%Set up shared variables with OUTFUN history.x = [];
history.fval = [];
%call optimization
options = optimset('largescale','off',...
'outputfcn',@outfun,'display','on');
[x,fval,exitflag,output]=fminunc(@rozen,x0,options);
disp('Xopt=');disp(x);disp('fopt=');disp(fval);
disp(output); [X,Y]=meshgrid(-4:0.05:4);Z=rozen_g(X,Y);[c,h]=contour...
(X,Y,Z,[5 12 70 120 200 300 450 600 800],'blue'); clabel(c,h,[70 300 600],'FontSize',7);
y=history.x(:,1);z=history.x(:,2); hold on;plot(y,z,'black.',y,z,'red-'); xlabel('x1');ylabel('x2'); text(x0(1)-0.1,x0(2)+0.2,'x0');
title('Minimization by fminunc for Rozenbrok'); function stop = outfun(x,optimValues,state)
stop = false; switch state
case 'init' hold off case 'iter'
%Concatenate current point and objective
%function value with history. x must be a row
%vector. history.fval=[history.fval;
%optimValues.fval]; history.x = [history.x; x];
end
end end
14
В этой программе функция Розенброка представлена в двух вариантах: как входной аргумент fminunc и для вырисовки ее контуров (линий уровня). Им соответствуют m-файлы rozen и rozen_g, приводимые ниже.
function f = rozen(x) f=100*(x(2)-x(1)^2)^2+(x(1)-1)^2; end
function f = rozen_g(X,Y) f=100*(Y-X.^2).^2+(X-1).^2; end
Примечание. Во втором варианте записи функции возведению в степень предшествует точка, что означает поэлементное действие, иначе MATLAB будет выполнять матричную операцию и выдаст ошибку.
Теперь для выполнения программы достаточно ввести в командное окно начальную точку и обращение к программе:
>>x0=[1 -3]; history = runfminunc(x0)
инажать ввод. Конечные результаты выводятся в командное окно, а линии уровня и траектория поиска – в графическое окно (рис. 2).
Численные результаты выполнения программы:
Xopt= |
|
|
0.9999 |
0.9998 |
|
fopt= |
|
|
8.3148e-009 |
|
|
output= |
|
|
iterations: 28 |
/число итераций |
|
funcCount: 105 |
/число вычислений функции |
|
stepsize: 1 |
/размер шага |
|
firstorderopt: 2.4548e-004 /оптимальность первого порядка
algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]
history =
x: [29x2 double] fval: [29x1 double]
15
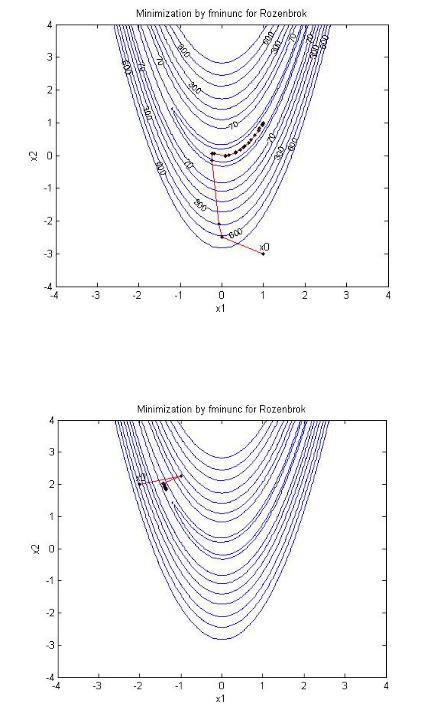
Рис. 2. Траектория поиска минимума методом BFGS
Как следует из отчета, функция fminunc по умолчанию использовала квазиньютоновский линейный алгоритм поиска минимума.
Рис. 3. Пример «застревания» поиска методом наискорейшего спуска
16
Если в аргументы optimset добавить параметр 'HessUpdate' со значением 'steepdesc', т.е. в качестве метода минимизации указать наискорейший спуск, то поиск из начальной точки (–2 2) застрянет вдали от минимума (рис. 3). Он также не достигнет минимума и из точки (1 –3). Причиной такого поведения метода является сильная овражность данной целевой функции.
2.2.Функция fminsearch
Вфункции fminsearch для нахождения минимума используется симплексный метод прямого поиска Нелдера – Мида. Изменение параметров производится посредством функции optimset. Параметры fminsearch Display, FunValCheck, MaxFunEvals, MaxIter,
OutputFcn, PlotFcns, TolFun и TolX идентичны одноименным параметрам для функции fminunc. Отличие только в меньшем числе функций графики: из перечисленных для fminunc в PlotFcns (см. прил. 1) используются первые три.
Обращение к функции возможно в следующих вариантах: x = fminsearch(fun,x0)
x = fminsearch(fun,x0,options) x = fminsearch(problem) [x,fval] = fminsearch(...)
[x,fval,exitflag] = fminsearch(...) [x,fval,exitflag,output] = fminsearch(...)
Смысл входных и выходных аргументов такой же, как в функции fminunc. Отличие в следующем. Fun может содержать только целевую функцию, и, соответственно, в выходных аргументах нет grad и Hessian, а exitflag может принимать только следующие значения: 1 – получено решение в результате сходимости процесса, 0 – число итераций превысило допустимое значение,
–1 – процесс остановлен функцией вывода (the output function).
Пример 3.
Найти минимум функции Розенброка
f(X) = 100( x2 – x12 )2 + ( x1 –1)2
с помощью fminsearch.
17
Запишем программу, как и в п. 2.1, в виде функции function history = runfminsearch(x0),
описание которой совпадает с приведенным для функции runfminunc, в нем заменяется только fminunc на fminsearch.
В командную строку заносим
>>x0=[1 –3];history = runfminsearch(x0),
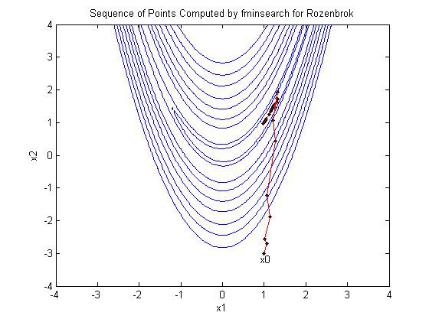
нажимаем Enter и получаем результаты в численном и графическом виде (рис. 4).
Рис. 4. Траектория поиска минимума методом Нелдера – Мида
Xopt=
1.0000 1.0000
fopt= 3.1666e-010 Output=
iterations: 56 funcCount: 105
algorithm: 'Nelder-Mead simplex direct search' message: [1x196 char]
18

Сравнивая результаты поиска fminunc и fminsearch из одной начальной точки (1 –3), видим, что во втором случае потребовалось в два раза больше итераций, но число вычислений функции оказалось одинаковым. Если начать поиск с точки (–2 2)
>> x0=[-2 2];history = runfminsearch(x0),
то получим следующие результаты:
Xopt=
1.0000 1.0000 fopt= 3.9243e-010 Output=
iterations: 112 funcCount: 208
algorithm: 'Nelder-Mead simplex direct search' message: [1x196 char]
Рис. 5. Поиск методом Нелдера – Мида из точки (–2 2)
Как видно из отчета и рис. 5, симплексный метод в отличие от метода наискорейшего спуска сходится к минимуму с высокой точностью.
19
Лабораторная работа № 1 Одномерная и безусловная оптимизация
Задания:
1.Ознакомиться с возможностями функций Toolbox Optimization для решения задач одномерной и безусловной многомерной минимизации и с методами, заложенными в них.
2.Воспроизвести пример 1, повторить с заменой числа 25 на 38; найти минимум этой же целевой функции без использования графики.
3.Найти минимум функции y = exp(sin(x)) + exp(–x) на интервале (–0,5pi, 3pi) без графики и с графикой.
4.Воспроизвести пример 2. Повторить для разных начальных точек, одна из которых (–2 2).
5.На функции Розенброка исследовать поведение метода наискорейшего спуска при разных начальных точках.
6.Для функции Розенброка применить метод DFP, используя несколько начальных точек.
7.Воспроизвести пример 3 и исследовать поведение метода Нелдера – Мида при разных начальных точках.
8. Найти максимум функции y |
|
|
10 |
|
. |
30(x |
x2 )2 |
5(1,5 x )2 |
1 |
||
2 |
1 |
1 |
|
|
|
9. Сделать выводы по применимости исследованных алгоритмов оптимизации.
20
