
Оптимизация в среде MATLAB
..pdf[X,FVAL,EXITFLAG,OUTPUT] = gamultiobj(...) [X,FVAL,EXITFLAG,OUTPUT,POPULATION] = gamultiobj(...) [X,FVAL,EXITFLAG,OUTPUT,POPULATION,SCORE] = ...
gamultiobj(...),
где FITNESSFCN – векторная фитнес-функция, X – множество локальных паретовских решений в виде матрицы с числом стобцов, равным числу переменных, и числом строк, равным числу решений, FVAL – матрица значений целевых функций в X (число столбцов равно числу целевых функций), EXITFLAG – содержит признак завершения алгоритма:
1 – среднее изменение размаха множества Парето за StallGenLimit поколений меньше TolFun,
0 – прошло максимальное число поколений, -1 – остановлено output или plot функцией, -2 – не найдено допустимой точки, -5 – исчерпан лимит времени,
POPULATION – конечная популяция, SCORE – значения целевых функций в конечной популяции; остальные аргументы описаны в предыдущих разделах.
Рассмотрим примеры применения ного нахождения множества Парето.
Пример 18.
Найти и построить множество Парето для двухмерной целевой функции
f (1 x )4 |
(x x )2 |
; |
f |
2 |
(4 x )4 |
(x x )2 . |
|||
1 |
1 |
2 |
1 |
|
|
2 |
2 |
1 |
|
Для решения задачи фитнес-функцию представим в виде m-файла:
function f = multifun(x); f(1)=(1-x(1))^4+(x(2)-x(1))^2; f(2)=(4-x(2))^4+(x(2)-x(1))^2; end
а для графических построений запишем два m-файла: fun1g и fun2g.
Составим программу, в которой все параметры установлены по умолчанию и только размер популяции увеличим до 70. Кроме того, предусмотрим построение линий уровня функций с последующим нанесением получаемых генетическим алгоритмом точек и точного мно-
121
жества Парето, а также отображение зависимости между целевыми функциями в окрестности Парето (границы Парето). В итоге приходим к следующей программе решения задачи:
options=gaoptimset('PopulationSize',70); [x,fval]=gamultiobj(@multifun,2,[],[],[],[],[],[],...
options); y=x(:,1);z=x(:,2);plot(y,z,'red.');hold on; [X,Y]=meshgrid(0:0.05:5);Z=fun1g(X,Y);
contour(X,Y,Z,[0.03 0.2 0.5 0.7 1 2 3 6 9 15 25 40...
55 80 115],'b');
hold on; [X,Y]=meshgrid(0:0.05:5); Z=fun2g(X,Y); contour(X,Y,Z,[0.01 0.05 0.1 0.3 0.6 1 2 3 6 9 15 20...
26 35 52 75 100 130],'g'); a=[1,1];
for k=1.1:.1:3.9 a=[a;[k,fzero(@(t)twograd([k,t]),[1,4])]];
end
a=[a;[4,4]];hold on;
plot(a(:,1),a(:,2),'k-');%Plot true Pareto frontier xlabel('x1'); ylabel('x2'); figure;plot(fval(:,1),fval(:,2),'r*');grid on; xlabel('f1');ylabel('f2');
В процессе выполнения этой программы выдавались значения целевых функций особей поколений, а в завершение – сообщение о причине останова алгоритма:
Optimization terminated: average change in the spread of Pareto solutions less than options.TolFun.
Но удобнее получить результаты в компактном виде, для чего исполним команду
>> [x,fval] ans =
x1 |
x2 |
f1 |
f2 /обозначения столбцов вписаны автором |
1.0078 |
1.0078 |
0.0000 |
80.1648 |
3.9370 |
3.9270 |
74.4067 |
0.0001 |
3.9726 |
3.9687 |
78.0856 |
0.0000 |
1.4641 |
2.1668 |
0.5402 |
11.7872 |
1.1310 |
1.1169 |
0.0005 |
69.0963 |
4.0288 |
4.0280 |
84.1553 |
0.0000 |
122
3.8881 |
3.8993 |
69.5701 |
0.0002 |
1.3991 |
1.7692 |
0.1623 |
24.9025 |
1.2630 |
1.3006 |
0.0062 |
53.1002 |
3.6214 |
3.6942 |
47.2294 |
0.0140 |
1.0399 |
1.0232 |
0.0003 |
78.5203 |
3.7828 |
3.8391 |
59.9763 |
0.0038 |
1.1747 |
1.1992 |
0.0015 |
61.5333 |
3.0694 |
3.5207 |
18.5429 |
0.2565 |
3.8449 |
3.8286 |
65.5032 |
0.0011 |
3.3862 |
3.5866 |
32.4608 |
0.0694 |
2.6681 |
3.3464 |
8.2021 |
0.6426 |
1.0078 |
1.0078 |
0.0000 |
80.1648 |
1.3987 |
1.6935 |
0.1122 |
28.3888 |
3.7134 |
3.7551 |
54.2090 |
0.0053 |
3.4833 |
3.5882 |
38.0383 |
0.0398 |
1.4262 |
2.0792 |
0.4594 |
14.0397 |
1.9411 |
2.5784 |
1.1906 |
4.4903 |
3.2271 |
3.4262 |
24.6421 |
0.1480 |
1.3915 |
1.4790 |
0.0312 |
40.3978 |
Из этих данных следует зависимость между целевыми функциями вблизи границы Парето, показанная на рис. 36. Мы видим, что при смещении вдоль границы Парето на малое расстояние от минимума одной из функций значение этой функции резко возрастает. Поэтому область приемлемых по обеим функциям решений очень узкая, а чувствительность функций к малым изменениям решения высокая.
На рис. 37 представлены контуры функций, на их фоне красными ромбиками показаны полученные точки, а сплошной черной кривой – точное множество Парето. Очевидно, что найденные точки лишь приближенно выделяют окрестность множества Парето, причем более точно вблизи экстремумов функций.
При двух гладких целевых функциях касательные к линиям уровня обеих функций в точках Парето совпадают (это точки касания линий уровня) и, следовательно, градиенты функций лежат на одной прямой, но направлены противоположно.
123
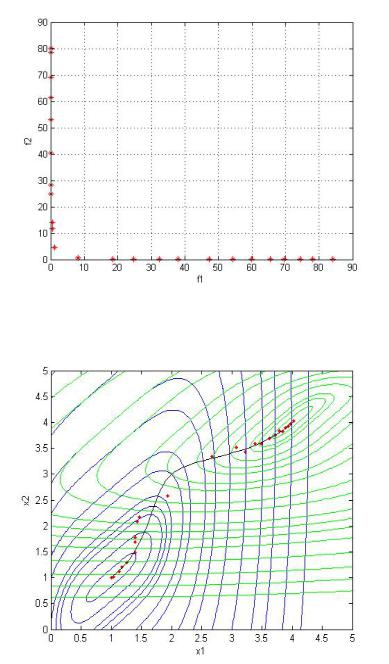
Рис. 36. Зависимость между целевыми функциями в окрестности границы Парето
Рис. 37. Приближенное и точное множество Парето в примере 18
124
Это свойство использовано при построении точного множества Парето и отражено в функции twograd, включенной в вышеприведенную программу.
function g = twograd(x) g1=[-4*(1-x(1))^3-2*(x(2)-x(1));
2*(x(2)-x(1))]; g2=[-2*(x(2)-x(1));-4*(4-x(2))^3+2*(x(2)-x(1))]; %Two gradients are opposite directed g=g2(1)*g1(2)-g2(2)*g1(1);
end
Равенство нулю последнего выражения означает противоположность градиентов, это условие реализовано в программе через функцию нахождения нулей fzero (см. п. 9.1).
Пример 19.
Найти и построить множество Парето для двухмерной целевой функции
f (1 x )4 |
(x x )2 |
; |
f |
2 |
(4 x )4 |
(x x )2 |
|||
1 |
1 |
2 |
1 |
|
|
2 |
2 |
1 |
|
при условии –0,9 x1 + x2 0,5.
В программу добавим элементы неравенства и отразим их в аргументах функции:
A=[0,9 –1]; b=[-0.5];
[x,fval]=gamultiobj(@multifun,2,A,b,[],[],[],[],...
options);
Исполнение программы завершается выводом сообщения о причине останова:
Optimization terminated: average change in the spread of Pareto solutions less than options.TolFun.
Результаты получаем выполнением команды
>> [x,fval] ans =
125
x1 |
x2 |
f1 |
f2 |
/обозначения столбцов вписаны автором |
1.6080 |
2.0703 |
0.3504 |
14.0794 |
|
1.2965 |
1.6659 |
0.1442 |
29.8177 |
|
2.0346 |
2.9904 |
2.0593 |
1.9525 |
|
1.8947 |
2.9204 |
1.6927 |
2.4107 |
|
1.7055 |
2.2954 |
0.5958 |
8.7901 |
|
2.1035 |
3.0104 |
2.3054 |
1.7814 |
|
1.5977 |
2.1671 |
0.4519 |
11.6097 |
|
2.1407 |
3.1933 |
2.8011 |
1.5315 |
|
1.3930 |
1.7553 |
0.1552 |
25.5174 |
|
1.6494 |
2.4291 |
0.7858 |
6.6976 |
|
1.6126 |
2.5345 |
0.9906 |
5.4628 |
|
1.6404 |
2.1131 |
0.3917 |
12.8992 |
|
1.7789 |
2.4984 |
0.8857 |
5.6018 |
|
1.9928 |
2.9385 |
1.8660 |
2.1638 |
|
1.6321 |
2.0156 |
0.3067 |
15.6546 |
|
1.6804 |
2.3968 |
0.7276 |
7.1192 |
|
2.0511 |
3.0349 |
2.1885 |
1.8354 |
|
1.5502 |
1.9582 |
0.2581 |
17.5471 |
|
1.3682 |
1.7308 |
0.1498 |
26.6487 |
|
1.8161 |
2.4536 |
0.8500 |
6.1247 |
|
1.8075 |
2.7281 |
1.2726 |
3.4647 |
|
1.4439 |
1.8010 |
0.1664 |
23.5100 |
|
2.1047 |
3.0824 |
2.4452 |
1.6648 |
|
1.5319 |
1.8804 |
0.2015 |
20.3077 |
|
1.4497 |
1.8216 |
0.1792 |
22.6574 |
|
Графическое представление зависимости функций показано на рис. 38. Ее использование позволит ЛПР достаточно просто найти наилучшее компромиссное решение. Расположение найденных решений относительно точного множества Парето дано на рис. 39. Здесь хорошо видно, как на решения повлияло линейное ограничение (граница допустимого множества решений показана малиновой линией).
126
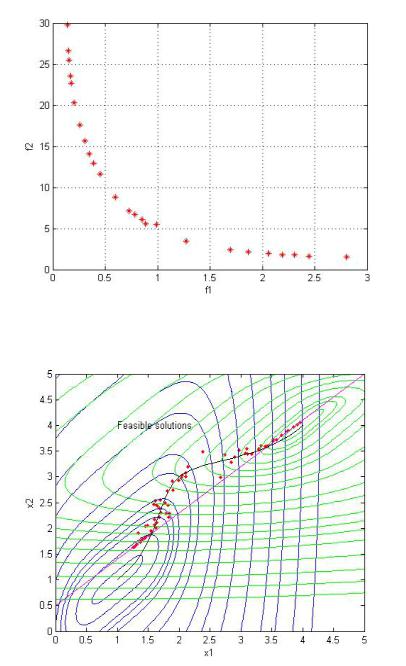
Рис. 38. Конечное приближение к границе Парето в примере 19
Рис. 39. Приближенное и точное множество Парето в примере 19
127

5.2. Метод достижения цели. Функция fgoalattain
Функция fgoalattain, входящая в пакет Optimization Toolbox, реализует метод достижения многомерной цели (целевого программирования). Идея метода состоит в том, что вместо непосредственной минимизации критериев цели ставится задача максимального достижения желаемых уровней этих критериев.
Пусть F(x) = (f1(x), f2(x), …, fm(x)) – вектор целевых функций, а goal = (goal1, goal2, …, goalm) – вектор заданных целевых значений, которые желательно достичь. Чем меньше разность fi(x) – goali, тем точнее достигается i-я цель. Для объединения целей следует использовать относительные разности, введя для этого вектор неотрицательных весов w = (w1, w2,…, wm). Обозначив максимальную относительную разность как γ, приходим к выводу, что для максимально возможного достижения целей необходимо минимизировать γ. Таким образом, задача достижения цели формулируется в виде
γ min,
x
F(x) – w·γ ≤ goal, A·x ≤ b,
Aeq·x = beq,
C(x) ≤ 0, ceq(x) = 0, lb ≤ x ≤ ub.
Первые m ограничений-неравенств называются целевыми ограничениями, но при задании задачи в fgoalattain они не входят в число оганичений, так как учитываются внутри алгоритма (в функции качества, подобной штрафной функции). Чем ближе вес wi к нулю, тем жестче целевое ограничение и тем выше требование к точности достижения i-й цели. Рекомендуется устанавливать w равным abs(goal), то-
гда F x – goal w
Следовательно, абсолютное значение γ при γ < 0 в оптимальном решении показывает максимальное относительное отклонение от цели среди всех целей. При отрицательном γ значения всех целевых функций лучше их целевых значений, а при положительном – значение по крайней мере одной целевой функции больше цели. Целевые функции, по которым целевые ограничения обращаются в равенства (они опреде-
128
ляют γ), называются активными. Через задание w ЛПР может оказывать влияние на степень достижения той или иной цели.
Функция fgoalattain использует метод последовательного квадратичного программирования (SQP) с модификацией в части линейного поиска и гессиана. В линейном поиске применяется функция качества вида
m
(x, ) ri max[0, fi (x) wi goali ],
i 1
апри действиях с гессианом учитывается его особая структура (нули в строках и столбцах, ассоциированных с переменной γ).
Заметим, что функция fgoalattain ориентирована на задачи с непрерывными целевыми функциями. Возможно получение решения и при нарушениях непрерывности, если они не будут проявляться в точках, из которых делается шаг вперед. Метод достижения цели дает локальный результат.
Решение задачи рассматриваемым методом начинается с установки желаемых параметров. Для этого применяется функция optimset. Краткое описание всех параметров fgoalattain и их значения по умолчанию приведены в прил. 7. Остановимся лишь на некоторых.
Если каких-либо целей требуется достичь максимально точно, соответствующие целевые функции размещают первыми в описании (m-файле) многомерной цели, а параметру GoalsExactAchieve придают значение, равное числу точных целей. Например, запись в командной строке
options = optimset('GoalsExactAchieve',2);
реализует требование, чтобы первые две цели достигались с максимально возможной точностью.
Параметры GradObj и GradConstr устанавливают в ‘on’, когда градиенты целевых функций и нелинейных ограничений задаются аналитически. При наличии нелинейных ограничений нельзя задать градиенты только целевых функций или только ограничений, так как в функции качества они представлены вместе. Градиент многомерной цели – это матрица, в которой каждый столбец есть градиент одной целевой функции (частные производные по всем переменным). Для ограничений имеем две матрицы, отдельно для неравенств и равенств. В каждой из них столбец матрицы содержит градиент соответствующей левой части ограничения (C(x) или ceq(x)). Аналитическое задание градиентов ускоряет процесс решения, в противном случае все произ-
129
водные вычисляются одним из методов конечных разностей, определяемым параметром FinDiffType. Напомним, что при аналитическом задании градиентов они описываются в одном m-файле с самой целевой функцией или функциями ограничений.
Синтаксис fgoalattain зависит от модели задачи и описания результата решения.
x = fgoalattain(fun,x0,goal,weight)
x = fgoalattain(fun,x0,goal,weight,A,b)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub) x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,...
lb,ub,nonlcon)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,...
lb,ub, nonlcon, options) x = fgoalattain(problem)
[x,fval] = fgoalattain(...) [x,fval,attainfactor] = fgoalattain()
[x,fval,attainfactor,exitflag] = fgoalattain(...) [x,fval,attainfactor,exitflag,output] = ...
fgoalattain(...) [x,fval,attainfactor,exitflag,output,lambda] = ...
fgoalattain(...)
Смысл входных аргументов очевиден. Заметим, что функция fun наряду с целевыми функциями может включать и градиенты. Точно так же функция nonlcon может содержать помимо функций нелинейных ограничений и их градиенты. Значения целей goal, как и начальную точку x0, задает ЛПР, а веса weight первоначально берут равными абсолютным значениям целей. Аргумент options обязателен, если изменены какие-либо параметры через optimset, при этом для отсутствующих аргументов устанавливается значение [].
Выходные аргументы x и fval содержат решение и вектор значений целевых функций. Аргумент attainfactor – это γ, величина которого показывает относительное отклонение от цели, лимитирующей дальнейшее повышение точности. Причина остановки алгоритма содержится в exitflag:
1 – установлена сходимость, 4 – величина направления поиска меньше допустимой и наруше-
ние ограничений меньше допустимого TolCon,
130
